3.2 Сходимость числовых последовательностей

Если изобразить элементы последовательности an на плоскости точками с координатами (n, an), то неравенства а — ε < an < а + ε означают, что все точки (n, an) с номерами n > N расположены между прямыми a —ε и а + ε, параллельные оси абсцисс.

Ниже приведен фрагмент рабочего документа Mathcad, в котором исследована сходящаяся последовательность и построен график, иллюстрирующий процесс сходимости.

Зададим последовательность и вычислим символьно её предел.

Последовательность СХОДИТСЯ, предел последовательности равен 1.

Найдём n = N(ε), для которого справедливо равенство

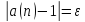
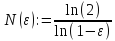
Вычислим значения N N(0.1) = 7.273

Неравенство

справедливо:

Для N > 7 при ε = 10ˉ¹

Последовательность {αn}, предел которой равен нулю называется бесконечно малой.

КЛАССИФИКАЦИЯ ТОЧЕК РАЗРЫВА.

ПОВЕДЕНИЕ ФУНКЦИИ НА ГРАНИЦАХ ОБЛАСТИ ОПРЕДЕЛЕНИЯ

Непрерывность и разрывы функции. Классификация разрывов

Рассмотрим функцию f(x) определенную на некотором промежутке (а, b) С R.

Функция f(x) непрерывна в точке X0 €(а, b), если предел функции в точке X0 равен значению функции в этой точке: lim f(x) = f(x,о).

Х-+Х0

Функция, непрерывная в каждой точке промежутка (а, Ь), назы­вается непрерывной на промежутке. Если функция f(x) определена на промежутке (a, b), b > а, то при исследовании поведения функции в окрестности точки а имеет смысл говорить о пределе функции f(x) в точке а справа, а при исследовании в окрестности точки b — о пределе функции f(x) в точке b слева*. Число А называется пределом справа функции f(x) при х, стремящемся к а, если для любого положительно­го числа £, как бы мало оно ни было, существует такое положительное число 6, что для всех х, удовлетворяющих неравенству а < х < а + д, справедливо неравенство | . В таких случаях говорят "пре­дел справа функции f(x) в точке а" и обозначают lim f(x) = А.

х-т+0

Пределы слева и справа называют односторонними пределами в точке.

Аналогично, говорят "предел слева функции f(x) в точке b" и обозначают если для любого положительного числа е, как бы мало оно ни было, существует такое положительное число b, что для всех х, удовлетворяющих неравенству b — 8 < х < b, справедливо неравенство .

Для существования предела функции в точке необходимо и до­статочно, чтобы существовали и совпадали односторонние пределы функции в этой точке.

По той же схеме вводится понятие непрерывности слева и непре­рывности справа. Функция, определенная на отрезке [а, b], b > а, непрерывна справа в точке а, если lim f(x) = f(a), и непрерывна

слева в точке 6, если lim f(x) = f(b). Для того чтобы функция была х—y→0

непрерывна в точке Xо, необходимо и достаточно, чтобы односторонние пределы функции в точке совпадали со значением функции в этой точке:

Если хотя бы одно из равенств нарушается, говорят о разрыве в точке xq.

Если и односторонние пределы конечны,

то разрыв в точке X0 называется устранимым.

, Аφ В, и оба односторонних предела конечны, то

говорят о скачке функции в точке. Устранимый разрыв и скачок называются разрывами первого рода.

Если один из односторонних пределов бесконечен или не существу­ет, то разрыв называется разрывом второго рода.

Так же, как для предела и непрерывности, говорят о разрыве слева и разрыве справа.

Ниже приведен фрагмент рабочего документа Mathcad, содержащий аналитическое и графическое исследование разрывов функции.

½

V(x) – 2

ЗАДАНИЕ 3.4

Найдите точки разрыва заданных функций и определите их тип.

Порядок выполнения задания:

1. Установите автоматический режим вычислений и режим ото­бражения результатов символьных вычислений по горизон­тали.

2. Определите выражение для функции.

3. Вычислите предел функции в точке разрыва.

4. Вычислите односторонние пределы функции в точке разрыва.

5. Постройте график функции в окрестности точки разрыва.

6. Сформулируйте вывод.

7. Выполните вычисления пп. 2-6 для всех функций из задания.

Пример выполнения заданияВариант исследования разрывов функций

(R) = 2^l/^x приведен выше. Все три функции имеют разрыв в точке х = 0. Функция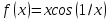 имеет в нуле устра­нимый разрыв. Положив /(0) = 0, получим непрерывную функцию. Функция имеет в нуле скачок. Функция v(x) - 2

имеет в нуле разрыв второго рода, поскольку бесконечен предел в нуле справа.

Непрерывные функции. Свойства непрерывных функций

Для функции, непрерывной на отрезке [а, b], справедливы следующие утверждения.

1. Функция, непрерывная на отрезке [а, b], достигает на нем своих наибольшего и наименьшего значений*, т.е. на отрезке [a, b] существуют точки х_т, хм такие, что

x€ [a,b]

m < f(x) <M, х€ [a, b].

2. Если функция f(x) непрерывна на отрезке [a, b] и принимает на концах значения разных знаков, то на интервале (a, b) существует точка с, в которой функция обращается в нуль, т.е. если f(a)f(b) < 0, то существует такая точка с G (а, b), что f(с) = 0.