1.2.2 Структура и свойства триангулярных борных слоев и кластеров

В результате обширных теоретических исследований борных кластеров [2-4, 29,30] было выявлено, что одной из наиболее стабильных и вероятных структур слоев из атомов бора должна быть триангулярная структура (рис. 1.2.1 б – верхний слой) [3, 31]. Эта структура представляет собой гексагональную сетку из атомов B с дополнительным атомом в центре каждого гексагона. Экспериментальные исследования малых борных кластеров, состоящих из 10-15 атомов, подтверждают эту точку зрения [32]. Можно предположить, что созданные из таких слоев борные нанотрубки также будут обладать высокой стабильностью [33-35].

Для четкого представления о характере связи в борных слоях, которая и определяет их высокую устойчивость, в работах [29, 30, 33, 34] были исследованы электронно-энергетические характеристики триангулярных борных слоев нескольких видов. Расчеты выполнялись при использовании теории функционала плотности [36-38]. Использованы приближение локальной плотности (LDA) [36, 39] и обобщенное приближение градиента (GGA) [40] для обмена и корреляции.

В таблице 1.2.1 приведены результаты расчетов для четырех различных борных плоскостей: плоские (flat triangular sheets) и гофрированные триангулярные слои (buckled triangular sheets) [33, 34], гексагональные слои, и так называемый α-слой, изображенный на рис.1.2.2 (А). Энергия связи Е_b вычислялась по формуле:

Е_b = Е_at - E_sheet, (1.3.1)

где Е_at - энергия изолированных спин-поляризованных атомов бора и E_sheet – энергия, приходящаяся на один атом слоя. Гофрированный триангулярный слой оказался более стабильным, чем плоский, за счет формирования сильных σ-связей [34]. При этом α-слой оказался самой стабильной структурой из рассмотренных. На рис.1.2.2 приведены два примера борных слоев, α- и β-слои, которые являются более стабильными, чем триангулярный слой. Все рассматриваемые борные слои оказались металлами [6].

Таблица 1.2.1 Основные электронно-энергетические характеристики плоских и гофрированных триангулярных борных слоев: Е_b - энергия связи, d^flat – длина связи в плоском триангулярном слое, d^σ и d^diag – длины связей в гофрированных триангулярных слоях, d^σ – расстояние между соседними атомами бора, находящимися на одной высоте, d^diag – расстояние между соседними атомами бора, находящимися на разных высотах, ∆z – высота гофры, d^flat – длина связи в борном гексагональном слое, d^new – длина связи в новом α-слое

	Плоский триангулярный слой		Гофрированный триангулярный слой
	Еb, эВ/атом	dflat, Ả	Еb эВ/атом	dσ , Ả	ddiag, Ả	∆z, Ả
LDA	6.58	1.68	6.74	1.59	1.80	0.81
Previous LDA [19]	6.76a	1.69	6.94a	1.60	1.82	0.82
Previous LDA [18]	6.53	-	6.79	-	-	-
GGA	5.79	1.70	6.00	1.60	1.86	0.88
Previous GGA [17]	5.48b	1.71	5.70b	1.61	1.89	-
	Гексагональный слой		α-слой
	Еb эВ/атом	dhex, Ả	Еb эВ/атом		dnew, Ả
LDA	5.82	1.65	6.86		1.64-1.67
GGA	5.25	1.67	6.11		1.66-1.69
Previous GGA [17]	4.96b	1.68	-		-

^a Энергия изолированного спин-поляризованного атома бора, составляющая 0,26 эВ/атом, объясняет различия между значениями Е_b, полученными в работах [34] и [33];

^b В то время, как значения Е_b из работы [27] не согласуются с результатами работы [33], значения Е_b плоского триангулярного и гексагонального слоев совпадают.

Рис.1.2.2 Примеры плоских борных слоёв: А – α-слой, Б – β-слой, параллелограммом выделена элементарная ячейка; В – четыре борных кластера: В₂₄(а) и В₃₂(а) – кластеры с гексагональной дыркой; В₂₄(б) и В₃₂(б) – двойные кольца кластеров [29,30]

Получить борные α- и β-слои можно путем удаления определенных атомов с поверхности плоского триангулярного слоя. Каждое удаление приводит к образованию «гексагональных дырок», в результате получается набор шестиугольников и треугольников. Для удобства, можно ввести такое понятие, как «плотность гексагональных дырок» η, которая определяется по формуле (1.2.2)

η = M / N (1.2.2)

где M – это число гексагональных дырок, а N - число атомов в оригинальном триангулярном слое.

Таким образом, триангулярный слой имеет η = 0, гексагональный η =1/3, а слои α и β - η =1/9 и η =1/7, соответственно.

A priori энергия таких слоев может зависеть как от значения η, так и от расположения шестиугольников. Это приводит к огромному разнообразию вариантов расположения гексагонов в триангулярном борном слое с одинаковым значением η. При заданном η наиболее стабильными будут структуры, в которых шестиугольники распределяются более равномерно. На рисунке 1.2.3 показана зависимость энергии связи Е_b от плотности «гексагональных дырок» η для рассматриваемого класса борных слоёв. Энергия Е_b достигает максимума в точке 6,86 эВ/атом при η = 1/9 (α-слой). Структура слоя типа β также оказалась более устойчивой, чем простая триангулярная структура с η ≈ 1/9, но менее устойчивой, чем α-слой.

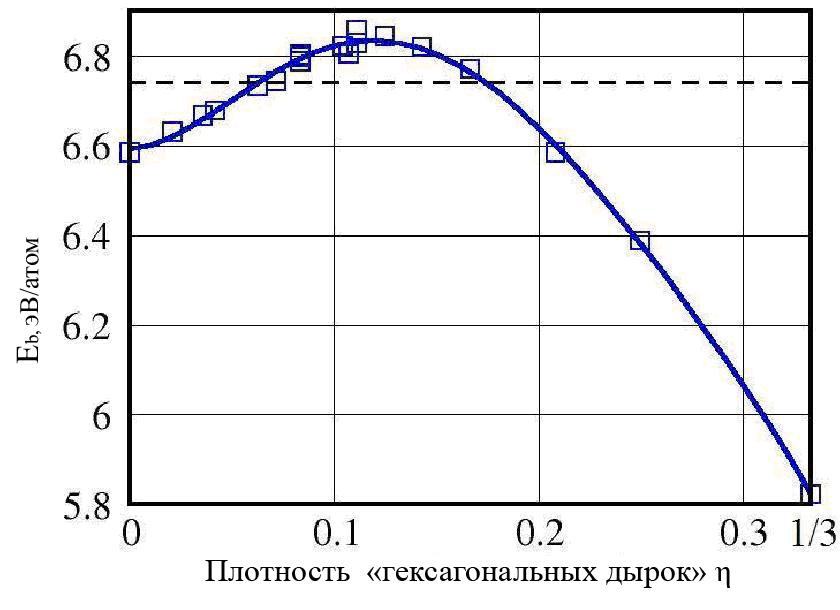
Рис.1.2.3 Зависимость энергии связи E_b от плотности гексагональных дырок в борных слоях η, равномерно распределенных по поверхности. Пунктиром показана энергия связи для гофрированного триангулярного борного слоя. Максимум на кривой соответствует энергии связи для α-слоя (η = 1/9) [6]

Для объяснения устойчивости структуры борного α-слоя следует рассмотреть характер его электронной связи. Как правило, связи в плоскости формируются за счет перекрытия sp₂ гибридных орбиталей, и это перекрытие сильнее, чем перекрытие π-связей, образованных из P_z-орбиталей. Таким образом, структуры, в которых оптимально заполнены электронные состояния в плоскости связей, должны быть наиболее устойчивыми. На рис. 1.2.4 показаны прогнозируемые плотности состояний (PDOS) пяти борных слоев в плоскости (сумма s, p_x и p_y) и вне плоскости (p_z) [6].

Рис. 1.2.4 Плотности состояний (DOS) для пяти конфигураций борных слоев: а) гексагональный, б) плоский триангулярный, в) гофрированный триангулярный, г) α-слой и г) β-слой, прогнозируемые для орбиталей, лежащих в плоскости слоя (сумма s, p_x и p_y) и вне плоскости (P_Z). Сплошной линией показаны проекции в плоскости, а пунктирной линией показаны проекции вне плоскости; жирной вертикальной линией показан уровень Ферми (E_F)

В гексагональном слое связи образованы sp₂-орбиталями. Все sp₂ гибридные орбитали ориентированы вдоль векторов, направленных в сторону ближайшего соседа так, что перекрытие гибридов образует каноническую двухцентровую связь. Между связанными состояниями в плоскости и несвязанными состояниями наблюдается большое расщепление уровней. P_Z-орбитали формируют свои собственные состояния из связанных и свободных состояний. Плотности состояний P_Z обращаются в нуль в точке перехода между ними. Так, в случае графена четыре валентных электрона атома полностью заполняют состояние SP₂ и состояние P_Z связи, что приводит к крайне стабильной структуре. Однако атом бора имеет только три валентных электрона. Как показано на рисунке 1.2.4, некоторые сильные sp₂-состояния являются незанятыми, что и объясняет неустойчивость такого графитоподобного борного слоя. Этот слой склонен к активному присоединению электронов извне, что приводит к увеличению стабильности.

В триангулярном борном слое (рис. 1.2.4) каждый атом имеет шесть ближайших соседей и только три валентных электрона. При таком строении борного слоя двухцентровая схема взаимодействия атомов уже не годится для описания взаимодействия между атомами. В работе [34] было предположено, что для описания подобных систем следует применять трехцентровую схему взаимодействия. На рисунке 1.2.5 показана возможная ориентация sp₂ гибридных орбиталей: три гибридных перекрытия находятся внутри равностороннего треугольника, образованного тремя соседними атомами (вершины данного треугольника).

Рис.1.2.5 Схема трехцентровой связи атомов бора в триагулярном плоском борном слое: слева показана ориентация sp₂ гибридных орбиталей; в центре и справа - перекрытие гибридных орбиталей в треугольнике (D3 симметрия), где b - одна связь орбиталей, а* - две антисвязи, которые вытянутся в ленты в результате взаимодействий внутри треугольника

В случае изолированного борного треугольника (рис. 1.2.5) мы имеем простую задачу с сильной связью 3х3 и с 3D-симметрией. Собственные состояния такой системы определены двумя фактами: одной низкоэнергетической симметрично связанной орбиталью b и двумя вырожденными высокоэнергетическими антисвязанными орбиталям а*. Это закрытые трехцентровые связи, более подробное описание которых дано в [41].

На рисунке 1.2.4 (б) можно видеть, что прогнозируемые плотности состояний обращаются в нуль в точке энергии разделения связанных и антисвязанных состояний. В идеале плоскость будет наиболее устойчива, если: (I) два электрона, участвующие в образовании связей, полностью заполнят b-подуровень, (II) для антисвязи a* подуровни будут пустыми, и (III) оставшийся электрон наполовину заполнит низкоэнергетический уровень р_z-связи. Это значит, что энергия Ферми E_F будет равна нулю в плоскости предполагаемых плотностей состояний, показанной на рисунке 1.2.4. Однако E_F лежит чуть выше своего идеального положения, и вследствие этого некоторые электроны находятся в неспаренных состояниях. Другими словами, триангулярный борный слой предпочитает выступать в роли донора, отдавая электроны с высокими значениями энергий.

Авторы [27] считают, что гексагональные борные слои смогут понизить свою энергию путем присоединения электронов, в то время как плоская триангулярная структура имеет избыток электронов в состояниях с антисвязями. Иными словами, плоские триангулярные борные слои должны являться донорами, а слои с двухцентровыми связями – акцепторами. Таким образом, если система будет являться смесью этих двух фаз в верном соотношении, то это позитивно скажется на стабильности обеих фаз. Плоскость, состоящая из смеси борных треугольников и шестиугольников, имеет наивысшую стабильность и может быть определена так: это такая система, в которой энергия Ферми близка к нулю и в которой заполнены все возможные спаренные состояния, а свободные состояния остаются незаполненными. Оставшиеся электроны заполнят низкоэнергетические p_z-состояния, что приведет к металлизации системы. Данные предположения хорошо подтверждаются видом кривых на рисунке 1.2.4 (г, д), а также энергетической стабильностью различных структур. На практике наиболее стабильная конфигурация α-слоя в точности удовлетворяет данным условиям, в то время как менее стабильный тип борного слоя β имеет небольшое отклонение значения энергии Ферми от идеального значения.

Данные исследования имеют важное значение для изучения борных кластеров, так как могут пролить свет на высокую устойчивость борного фуллерена В₈₀, состоящего из триангулярной сетки с дырками из пятиугольников [42]. Такая структура борного фуллерена привела к идеальному балансу между трехцентровыми и двухцентровыми борными связями.