§ 2.8. Анализ локальной оптимальности дифференциальной игры

Учитывая, что при , значение матрицы стремится к решению алгебраического уравнения (2.57) в начале координат

, (2.63)

т.е. . При этом матрицы , , а матрица

(2.70)

остается, по крайней мере, положительно полуопределенной.

Таким образом, в малой окрестности нуля система с управлением, реализованным с использованием SDRE-метода, сколь угодно близка линейной оптимальной системе

. (2.71)

Это приближение является асимптотически оптимальным в том смысле, что управление сходится к оптимальному при . Вслед за [36] найдем необходимые условия оптимальности регулятора нелинейным объектом в постановке дифференциальной игры. При этом будем полагать, что справедливы все предположения, сделанные в § 2.7.

Предположение 2.8.1. Матрицы вместе с градиентами , где

, , , , , , − элементы соответствующих матриц, непрерывны и ограничены .

Теорема 2.8.1. В общем многомерном случае () SDRE-управление нелинейным объектом

(2.72)

определяется необходимым условием оптимальности:

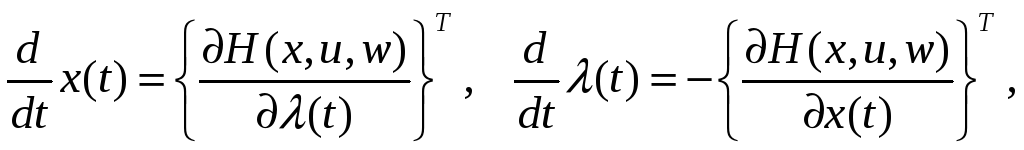(2.73)

, (2.74)

при этом, если выполняется предположение (2.8.1), второе уравнение (2.74) выполняется асимптотически с квадратичной нормой.

Доказательство. Запишем гамильтониан

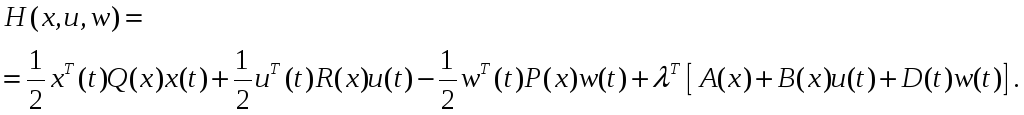(2.75)

Используя (2.74) и второе уравнение (2.73), будем иметь

, (2.76)

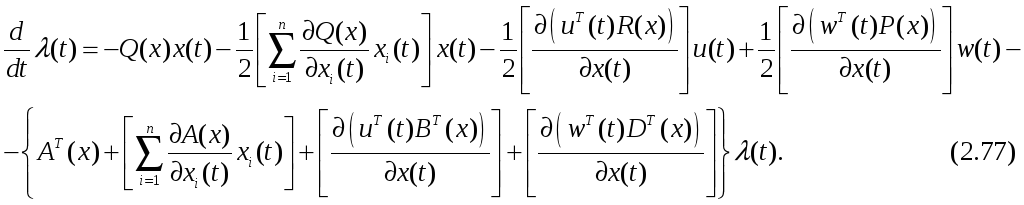
Вектор определялся ранее в виде . В силу этого

. (2.78)

Учитывая (2.72), (2.76) и приравнивая (2.77) и (2.78), получим

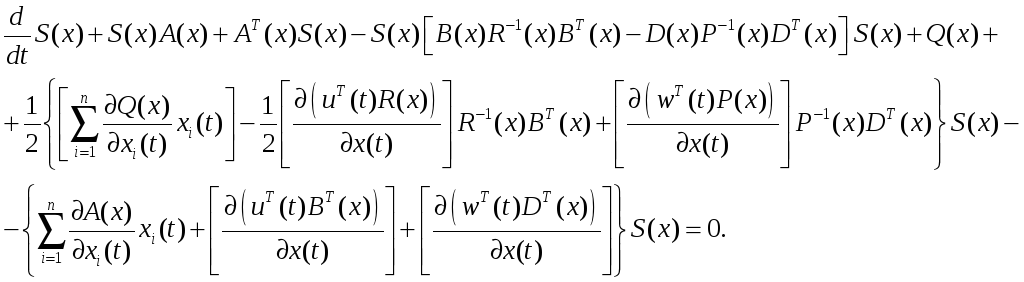
Если уравнение

(2.79)

поточечно определяет положительно определенную матрицу при , то уравнение

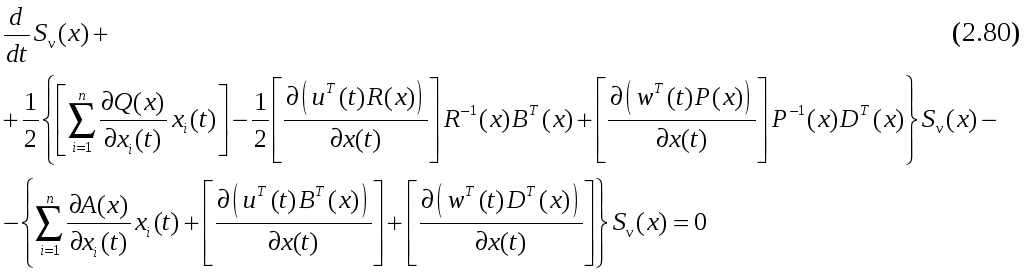
с начальным условием , определяемым решением уравнения

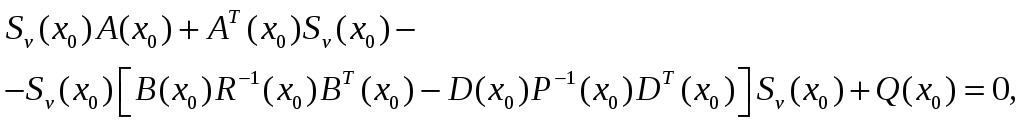
определяет динамику изменения матрицы при .

§ 2.9. Множество стабилизирующих управлений

В последние два десятилетия для построения управлений неопределенными объектами интенсивно развивается теория робастного управления. Наибольшие успехи в этой области достигнуты для анализа робастной устойчивости и робастной стабилизации линейных объектов.

Сравнительно недавно теория робастных систем пополнилась новыми инструментами синтеза регуляторов. Для линейных неопределенных систем это алгебраическое неравенство Риккати (Algebraic Riccati Inequality ,АRI), для нелинейных – неравенство Гамильтона-Якоби (Hamilton-Jacoby, HJI) [34,46]. HJI является скалярным неравенством с частными производными, что затрудняет применение этого метода. Одним из возможных способов нахождения робастного управления с использованием HJI является метод, основанный на аппроксимации HJI рядом Тейлора вокруг точки равновесия. Однако метод, основанный на представлении неравенства с частными производными с использованием аппроксимации возле точки равновесия, не позволяет получить более общие решения. С другой стороны, использование нелинейных матричных неравенств дает возможность исследовать системы, параметры которых зависят от состояния. Этот тип нелинейных обыкновенных дифференциальных уравнений позволяет перейти при синтезе робастного управления от использования неравенства Гамильтона-Якоби к неравенству Риккати с параметрами, зависящими от состояния объекта (State Dependent Riccati Inequality, SDRI). Другим словами, если существует положительно определенная матрица , параметры которой зависят от состояния объекта, и которая удовлетворяет неравенству Риккати (SDRI) и существует положительно определенная скалярная функция , удовлетворяющая решению , тогда эта функция удовлетворяет неравенству Гамильтона-Якоби (HJI).

Следует отметить, что использование метода SDRI для решения HJI наталкивается на проблему неоднозначного представления нелинейной системы в форме SDC [43]. Таким образом, решение SDRI может дать различные положительно определенные матрицы .

Добавим, что АRI и HJI невозможно использовать для решения терминальных задач управления неопределенными объектами. В последующих главах будет предложен метод синтеза робастного управления для нелинейного неопределенного объекта с параметрами, зависящими от его состояния (SDC), и заданным временем переходного процесса.

Рассмотрим управляемую и наблюдаемую систему, параметры которой в явном виде не зависят от времени

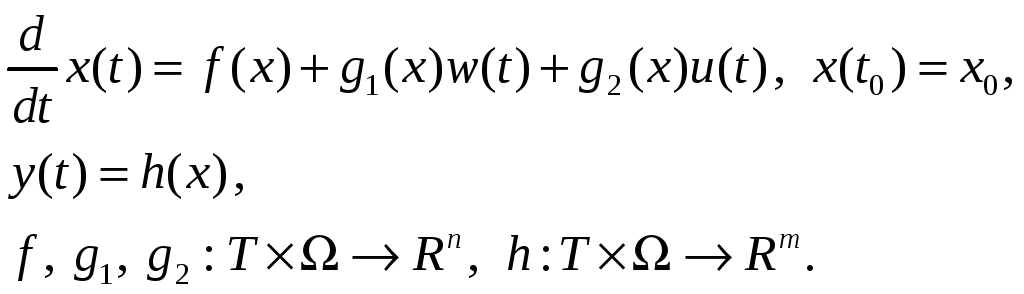(2.81)

Запишем неравенство Гамильтона-Якоби-Беллмана [42] для системы (2.81)

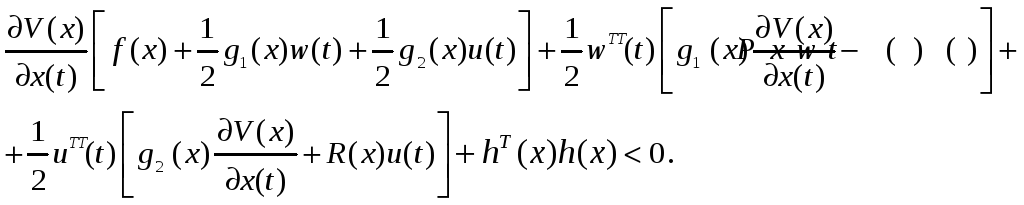(2.82)

Управления

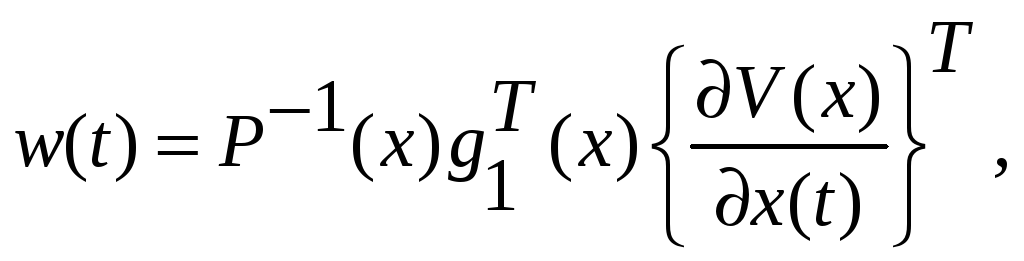
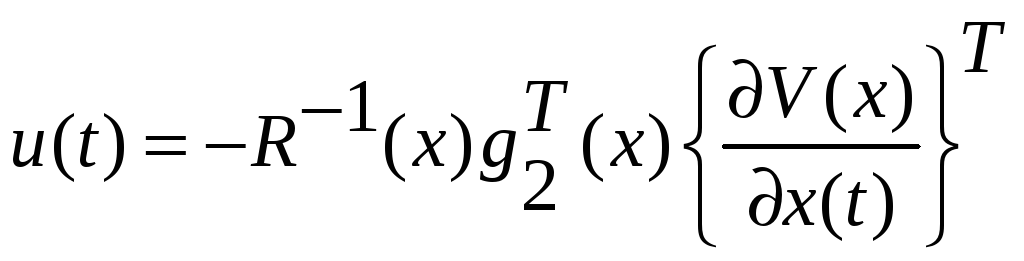(2.83)

вместе с вектором , удовлетворяющем неравенству (2.82), образуют множество управлений стабилизирующих объект (2.81).

Пусть объект (2.81) представим в виде

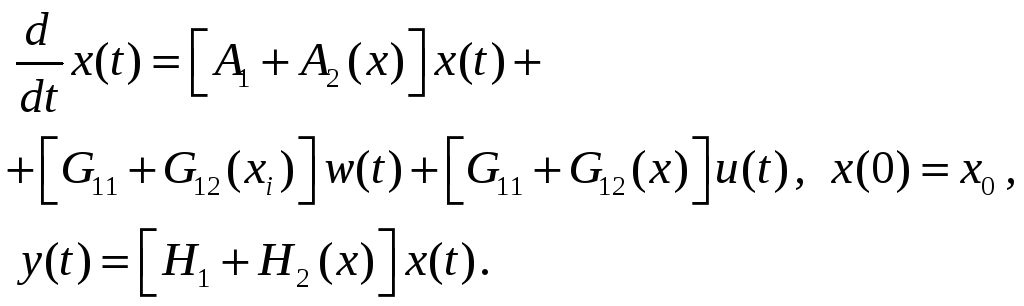_(2.84)

Запишем неравенство (2.82) с учетом (2.84)

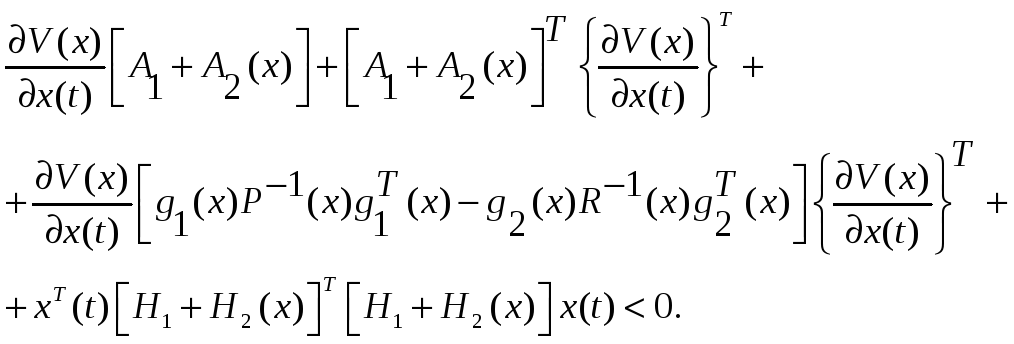(2.85)

Будем искать в виде

. (2.86)

Из (2.85) получим

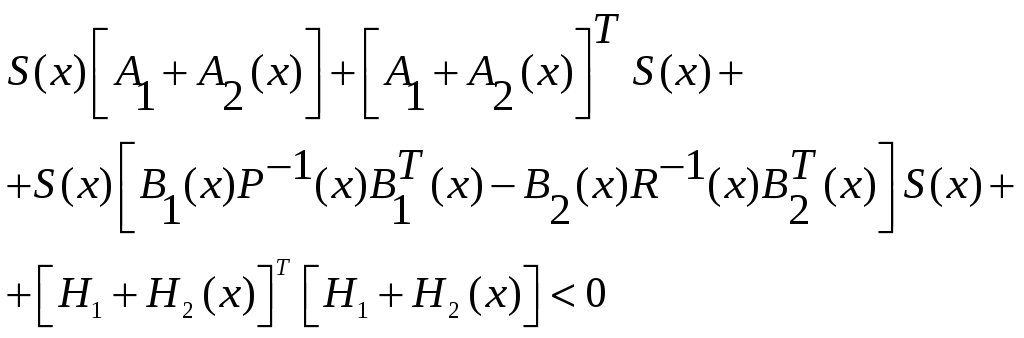(2.87)

или используя лемму Шура [7,43], преобразуем нелинейное неравенство (2.87) в линейное матричное неравенство

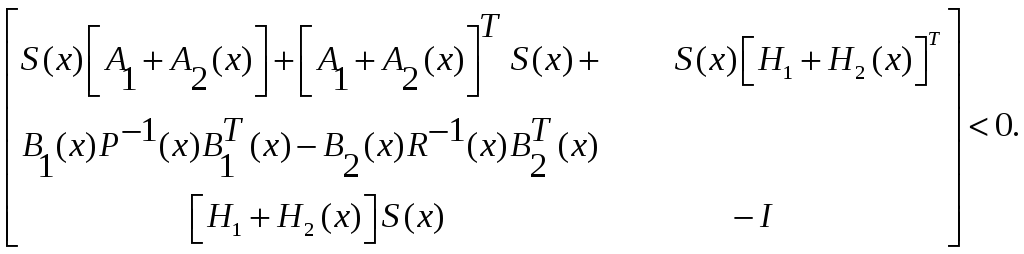(2.88)

Управления, обеспечивающие стабилизацию системы (2.84), принимают вид

, . (2.89)

Учитывая, что при , значение матрицы в начале координат должно быть таким, чтобы выполнялось неравенство

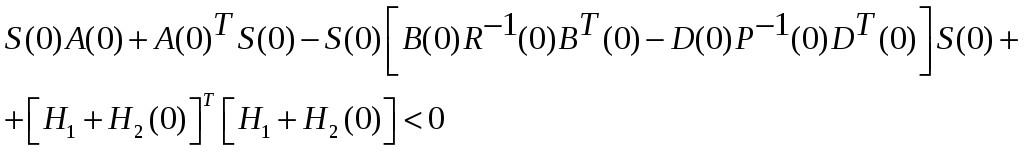(2.90)

или

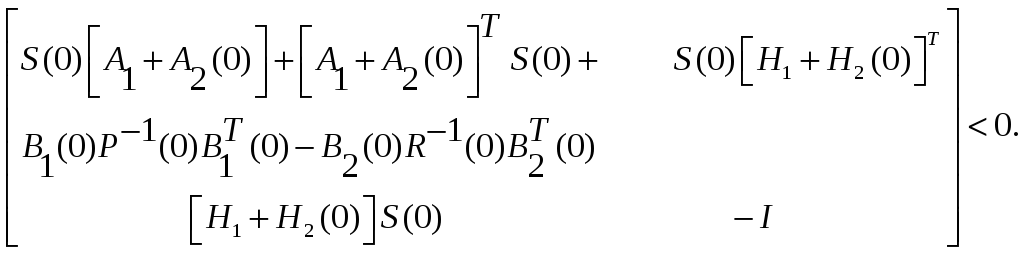(2.91)

При этом матрицы такие, что а матрица

(2.92)

остается, по крайней мере, положительно полуопределенной.

Управления (2.89) с матрицей , удовлетворяющей нелинейному матричному неравенству (2.87) или линейному матричному равенству (2.88), образуют множество стабилизируемых воздействий на систему

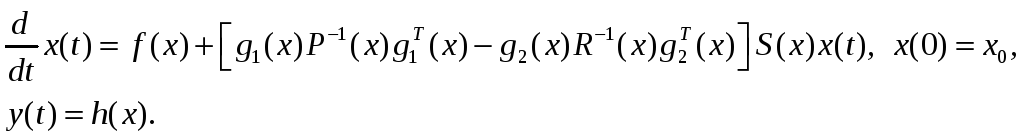(2.93)