§ 2.3. Оптимальные стратегии дифференциальной игры

При установлении условия существования оптимальных управлений в дифференциальной игре будет обобщена лемма [47].

Лемма 2.3.1. Пусть − действительный вектор, − действительные вектор-функции, − действительная функция, определенная на и ─ действительная положительно полуопределенная симметрическая матрица. Тогда уравнение

(2.21)

имеет решение относительно в виде

, (2.22)

если и только если

, (2.23)

где

. (2.24)

Здесь и − псевдо обратные (по Муру-Пенроузу) [11] матрицы от и , где вектор, входящий в так, что

. (2.25)

Доказательство. Подставив (2.22) в (2.21), будем иметь

или

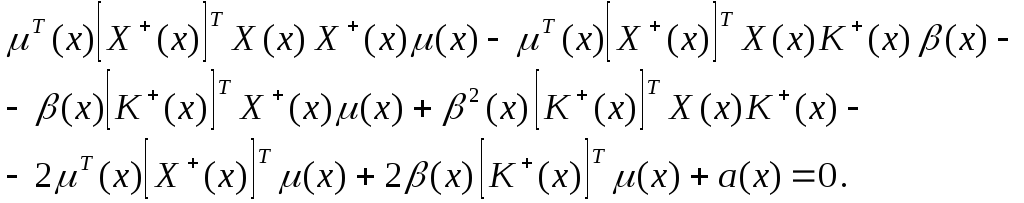
Учитывая, что , , где ─ единичная матрица, , получаем

. (2.26)

Откуда

.

Этим получены достаточные условия существования , как решения уравнения (2.21).

Используя уравнение (2.24), получим необходимые условия выполнения Леммы 2.3.1. Добавим и вычтем в левой части уравнения (2.26) выражение . Будем иметь

. (2.27)

Подставляя в (2.27) выражение для , получаем , так как .

Сделаем некоторое добавление к Лемме 2.3.1 для случая, когда положительно определенная матрица обратима.

Добавление 2.3.1. Пусть симметричная положительно определенная действительная матрица обратима для всех .

Тогда уравнение (2.21) имеет решение относительно в виде , (2.28)

где

, (2.29)

если и только если

. (2.30)

Здесь вектор входит в так, что .

Доказательство. Это следует из Леммы 2.3.1.

Следствие 2.3.1. Если положительно определенная матрица представима в виде

,

где матрицы и , то из (2.29) следует, что

. (2.31)

Следующая теорема, сформулированная с использованием Кронекеровского произведения, устанавливает условия существования оптимальных управлений в дифференциальной игре.

Теорема 2.3.1. Пусть для системы

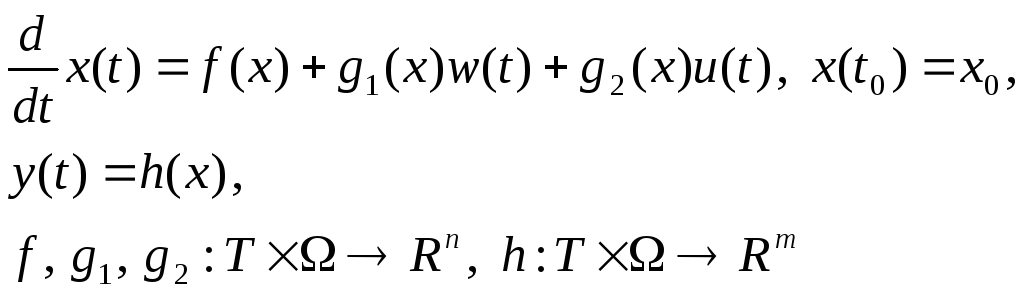
с функционалом

существует положительно определенная дважды дифференцируемая функция , удовлетворяющая уравнению Гамильтона-Якоби-Беллмана

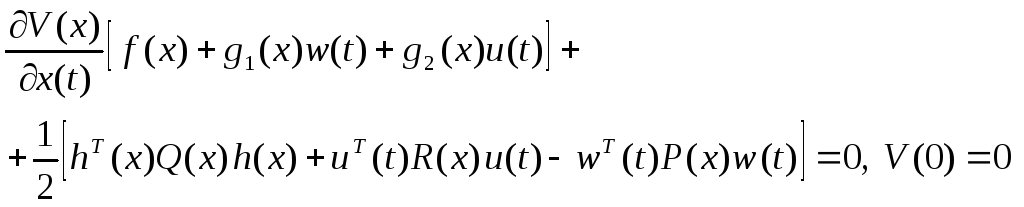
и

,

где − коммутирующий вектор, параметры которого принимают значения , определяемые при анализе устойчивости системы.

Тогда оптимальные управления и определяются выражениями

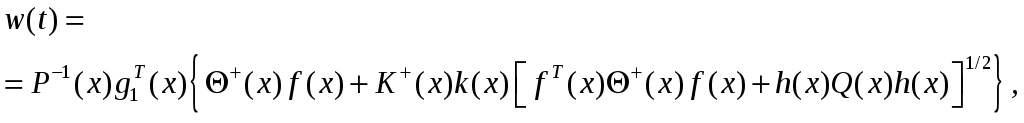
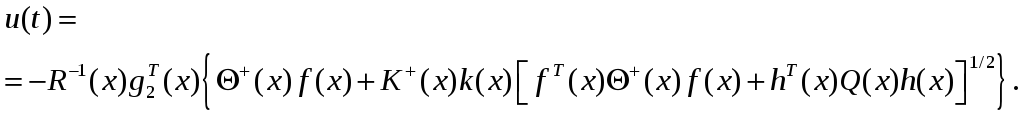
где и , если выполняются соотношения

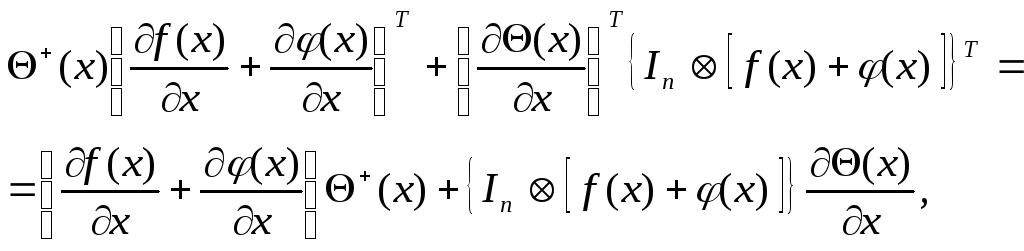
Здесь ─ единичная матрица, ─ символ Кронекеровского произведения.

Доказательство. Для доказательства теоремы 2.3.1 используем Лемму 2.3.1. Пусть

, , ,

и .

Тогда условие (2.21) обретает вид уравнения Гамильтона-Якоби

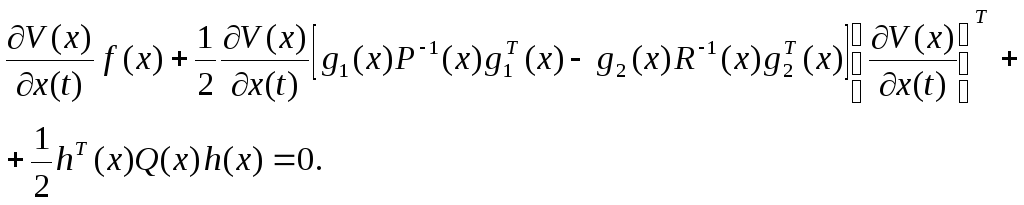
Решение (2.21) в терминах постановки задачи управления имеет вид

.

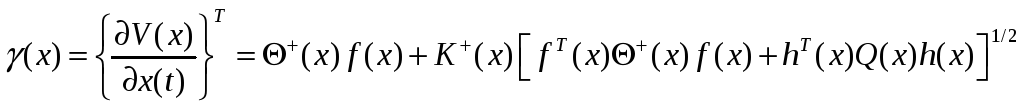Таким образом, учитывая (2.8),

(2.32)

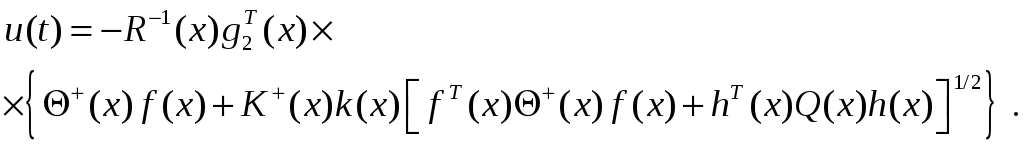(2.33)

Траектория движения системы (2.1) под воздействием оптимальных управлений (2.32), (2.33) будет являться решением дифференциального уравнения

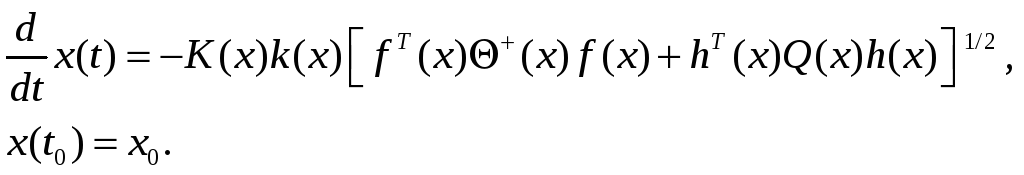(2.34)

Замечание 2.3.1. В задаче управления линейным объектом

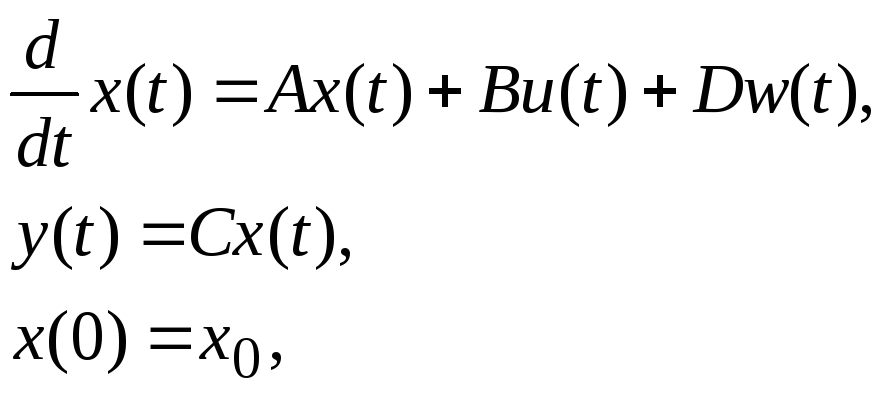(2.35)

где матрицы , , и имеют соответствующие размерности: , , , , с функционал качества

условие (2.28)

при назначении функции как

перепишется в виде

.

Откуда

.

Оптимальные управления определяются соотношениями [19]:

, .

Функционал качества принимает конечное значение

.