2. Експериментальне визначення ємності конденсаторів

Одним з експериментальних методів визначення ємності конденсаторів є метод порівняння їх невідомої ємності С_Х з відомою С_О. Електрична схема, з допомогою якої здійснюється таке порівняння отримала назву місткової схеми (або просто - містка). В містковій електричній схемі для визначення ємності конденсатора використовується властивість конденсатора пропускати змінний струм. Так, якщо конденсатор приєднати до джерела змінного струму, то обкладинки конденсатора будуть перезаряджатись і в колі виникне змінний струм, який залежить від напруги та від опору, що чинить даний конденсатор змінному струму. Опір конденсатора в колі змінного струму отримав назву реактивного ємнісного опору і значення цього опору визначається співвідношенням (34.11), де С - ємність конденсатора,  - частота струму. Тому, якщо маємо конденсатор невідомої ємності С_Х та відомої - С_О, то, порівнявши їх реактивні опори згідно (34.11), відношення ємностей цих конденсаторів буде (34.12).

(34.11)

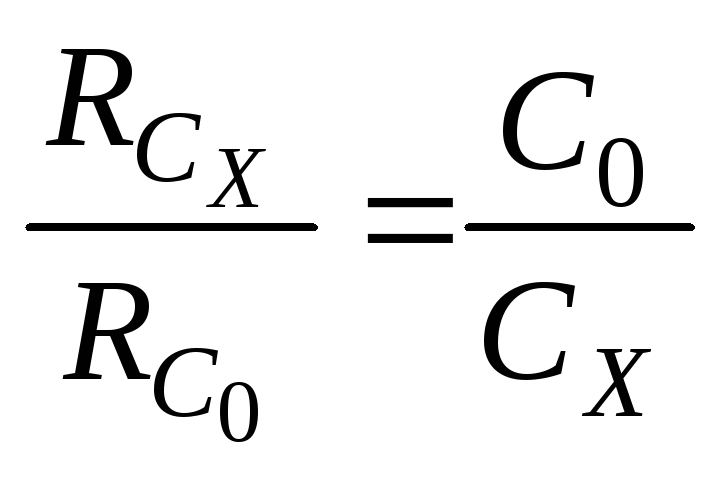(34.12)

На рис. 34.2 приведена схема містка Сотті, який дає можливість порівняти реактивні опори конденсаторів, а значить, їх ємності. Конденсатор невідомої ємності С_Х та відомої С_О мають спільну точку Е. Ці конденсатори другими кінцями приєднуються, як вказано на схемі, до реохорда АВ, який являє собою калібровану дротину. Вздовж реохорда переміщається рухомий контакт D. Між цим контактом та точкою Е вмикають змінну напругу (=50 Гц), конденсатори перезаряджаються і в колі виникає змінний струм.

Пересуваючи рухомий контакт D, на реохорді АВ знаходять таке його положення, коли потенціали _А та _В точок А і В стануть однаковими. Такий стан місткової схеми називають рівновагою містка, який легко виявити нуль-індикатором (Н-І) - гальванометром, що фіксує наявність або відсутність напруги (або струму).

Умову рівноваги містка Сотті можна вивести, користуючись законом Ома для окремих ділянок даної схеми. Так, якщо значення струмів в лівій і правій частинах містка відповідно рівні І₁ та І₂ , то одержимо чотири рівняння (34.13), (34.14), (34.15), (34.16) з закону Ома,

(34.13)

(34.14)

(34.15)

(34.16)

де R_СХ, R_С0 - реактивні опори конденсаторів; R_AD, R_DB - опори відповідних частин реохорда; _A, _B, _D, _E - потенціали відповідних точок схеми (_A =_B).

(34.17)

З системи рівнянь (34.13) - (34.16) випливає умова (34.17) рівноваги містка Сотті. Враховуючи співвідношення (34.12) і замінивши відношення опорів R_AD/R_DB частин реохорда відношенням їх довжин , отримаємо формулу (34.18) для визначення ємності невідомого конденсатора.

(34.18)

Відрізки та називають плечами реохорда. Таким чином, для визначення невідомої ємності С_Х за допомогою містка Сотті необхідно добитись умови його рівноваги - знайти на реохорді АВ таке положення рухомого контакту D, при якому різниця потенціалів між точками А і В рівна нулю, що засвідчить своїми показами нуль-індикатор. Вимірявши при цьому відповідні плечі реохорда та реохорда АВ та, знаючи величину відомої ємності С_О, за формулою (34.18) розраховують досліджувану невідому ємність.