2.7 Выбор тренда, наилучшим образом аппроксимирующего исходный временной ряд

Аппроксимация (приближение) − это замена исходных данных наиболее близкими к ним другими данными, представленными в виде тренда.

Для выбора трендовой модели, которая наилучшим образом аппроксимировала бы исходные данные, используются различные критерии, например, критерий наименьшей суммы квадратов отклонений.

Поскольку сравниваются трендовые модели, у которых одинаковое число параметров ( , ), то критерий наименьшей суммы квадратов отклонений будет иметь следующий вид:

.

Для проведения промежуточных расчетов построим таблицу:

Таблица 8

t	yt
1	7,9	8,04	8,1605	0,0196	0,0679
2	8,6	7,73	7,7525	0,7569	0,7183
3	7,3	7,42	7,3651	0,0144	0,0042
4	6,8	7,11	6,9966	0,0961	0,0387
5	5,9	6,8	6,6469	0,8100	0,5579
6	6,2	6,49	6,3145	0,0841	0,0131
7	6,7	6,18	5,9984	0,2704	0,4922
8	5,8	5,87	5,6986	0,0049	0,0103
9	6,0	5,56	5,4134	0,1936	0,3441
10	5,2	5,25	5,1428	0,0025	0,0033
11	5,0	4,94	4,8860	0,0036	0,0130
12	4,4	3,72	4,6420	0,4624	0,0586
-	75,80	75,11	75,073	2,7185	2,3214

Рисунок 6

Сравним значения критерия наименьшей суммы квадратов отклонений для линейного, степенного и показательного трендов:

Для линейного тренда критерий равен 2,7158, для показательного 2,3214. Коэффициент для показательного тренда меньше, чем для линейного , поэтому показательный тренд лучше аппроксимирует исходные данные.

Следовательно, для прогнозирования необходимо взять показательный тренд .

2.8 Расчет величины еt и адекватности выбранной модели тренда на основе условий

После того как была выбрана трендовая модель, имеющая наилучшую степень аппроксимации к исходным данным, необходимо оценить адекватность выбранного тренда тенденции исходных данных. ()

Чтобы оценить адекватность выбранной трендовой модели теоретическому тренду временного ряда, найдем разность е_t между исходными данными у_t и нашей трендовой моделью :

.

Таблица 9

t	Y(t)		et
1	7,9	8,1605	-0,2605
2	8,6	7,7525	0,8475
3	7,3	7,3651	-0,0651
4	6,8	6,9966	-0,1966
5	5,9	6,6469	-0,7469
6	6,2	6,3145	-0,1145
7	6,7	5,9984	0,7016
8	5,8	5,6986	0,1014
9	6,0	5,4134	0,5866
10	5,2	5,1428	0,0572
11	5,0	4,8860	0,114
12	4,4	4,6420	-0,242
-	-	-	0,7827

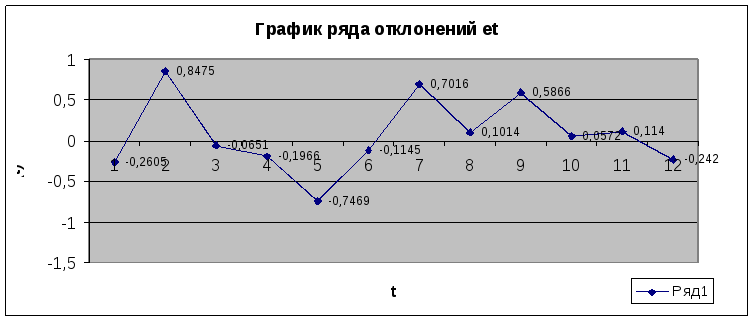
Рисунок 7

Условие 1. Колебание величины е_t должно носить случайный характер. Это условие означает, что колебание (изменение) величины е_t не содержит элементов тенденции. Проверим данное условие с помощью критерия поворотных точек.

Величина е_t считается поворотной, если она соответствует одному из двух условий: е_t-1< е_t >е_t+1 или е_t-1> е_t <е_t+1 .

Для расчетов построим таблицу:

t	Y(t)		et	Pt	et²	ē	(et-ē)²	(et-et-1)²
1	7,9	8,1605	-0,2605	-	0,0679	0,0652	0,10608	-
2	8,6	7,7525	0,8475	1	0,7183	0,0652	0,61199	1,2277
3	7,3	7,3651	-0,0651	0	0,0042	0,0652	0,01698	0,8328
4	6,8	6,9966	-0,1966	1	0,0387	0,0652	0,06854	0,0173
5	5,9	6,6469	-0,7469	1	0,5579	0,0652	0,65951	0,3028
6	6,2	6,3145	-0,1145	0	0,0131	0,0652	0,03229	0,3999
7	6,7	5,9984	0,7016	1	0,4922	0,0652	0,40500	0,6660
8	5,8	5,6986	0,1014	1	0,0103	0,0652	0,00131	0,3602
9	6,0	5,4134	0,5866	1	0,3441	0,0652	0,27186	0,2354
10	5,2	5,1428	0,0572	1	0,0033	0,0652	0,00006	0,2803
11	5,0	4,8860	0,1140	1	0,0130	0,0652	0,00238	0,0032
12	4,4	4,6420	-0,242	-	0,0586	0,0652	0,09437	0,1267
-	-	-	0,7827	8	2,3214	-	2,2704	4,4525

Таблица 10

По данным таблицы 10 построим график в соответствии с рисунком 7 и с помощью формул:

е_t-1< е_t >е_t+1 или е_t-1> е_t <е_t+1 .

определим поворотные точки.

Для проверки выполнения условия 1 выдвинем нулевую гипотезу Н₀: колебание величины е_t носит случайный характер.

Чтобы проверить нулевую гипотезу, вначале определим математическое ожидание числа поворотных точек

,

и его дисперсию

.

Кроме того, для проверки нулевой гипотезы используем вероятность, равную 95%, которой соответствует коэффициент доверия t=1,96. С помощью формулы

проверим нулевую гипотезу, подставив в нее значения М(Р), D(P), t :

или 4,029<8<9,304.

Расчет показывает, общее число поворотных точек – 8 находится в требуемом интервале. Это позволяет сделать следующий вывод: с вероятностью 95% колебание величины е_t носит случайный характер и, следовательно, отвечает данному условию.

Условие 2. Распределение величины е_t соответствует нормальному распределению. Данное условие проверяется с помощью RS-критерия.

Вначале определим среднее квадратическое отклонение:

а затем расчетное значение критерия RS_р, найдя предварительно в графе 4 таблицы 10 максимальное e_max=0,8475 и минимальное e_min=−0,7469 значения:

Следующим шагом проверки условия 2 является нахождение табличного значения RS-критерия – RS_T по приложению 3.

В таблице приводятся нижнее и верхнее значения RS-критерия для n=10 и n=20; а у нас n=12. Для нахождения нижнего и верхнего значений RS-критерия для n=12 используем принцип интерполяции.

В результате расчета нижнее значение RS_12Н = 2,772, а верхнее − RS_12B = 3,978.

Выдвинем нулевую гипотезу Н₀: величина е_t соответствует нормальному распределению.

Сопоставим по формуле:

RS_nн< RS_р< RS_nв

расчетное значение критерия RS_р с табличным –RS_Т..

Сопоставление показывает, что RS_р можно сказать попадает попадает в интервал, определяемый нижним и верхним табличными значениями RS-критерия, т.е. 2,772<3,3093<3,978. Это позволяет нам сделать следующий вывод: с вероятностью 95% нулевая гипотезе принимается, т.е. величина е_t соответствует нормальному распределению и, следовательно, отвечает условию 2.

Условие 3. Математическое ожидание величины е_t равно нулю. Для проверки данного условия выдвинем нулевую гипотезу Н₀: Ме_t=0, т.е. математическое ожидание е_t =0.

Вначале определим среднюю арифметическую величину е_t, использовав итог графы 4 таблицы 10;

.

Далее определим среднее квадратическое отклонение, использовав итог графы 8 таблицы 10:

.

Теперь найдем расчетное значение величины t_p:

.

Чтобы найти табличное значение величины t_T, зададимся уровнем значимости а=0,05, относительно которого определим доверительную вероятность γ=1−0,05=0,95, а также число степеней свободы k=12–1=11. Теперь, зная γ и k, определим t_T по Стьюденту (см. приложение 2); t_Т = =2,201. Сопоставим расчетное t_p=0,1389 и табличное t_T=2,201 значения:

t_p < t_T или 0,4971 < 2,201.

Сопоставление показывает, расчетное значение меньше табличного.

Это позволяет нам сделать следующий вывод: с вероятность 0,95 (95%) нулевая гипотеза принимается и мы можем утверждать: математическое ожидание е_t =0.

Условие 4. Независимость членов ряда друг от друга. Это условие означает отсутствие автокорреляции во временном ряде е_t.

По итоговым значениям граф 6 и 9 определим расчетное значение критерия Дарбина–Уотсона d_p:

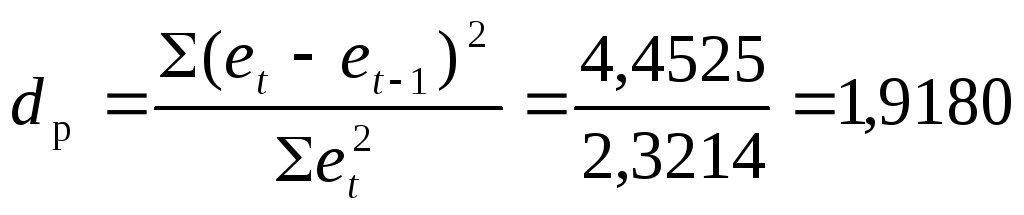
Найдем табличное значение критерия Дарбина–Уотсона d_T при n=12, и числе факторов в используемой трендовой модели V=1.

При n=12 и V=1 в приложении 4 находим табличное значение критерия Дарбина–Уотсона d_T.

Однако у нас n=12, а в таблице наименьшее значение n=15, поэтому возьмем табличное значение критерия Дарбина–Уотсона для n = 15. Его нижнее значение равно d₁=1,08, а верхнее d₂=1,36. Сопоставим расчетное (1,9180) и табличное (1,08; 1,36) значения критерия Дарбина–Уотсона.

Мы видим, что расчетное значение больше верхнего табличного, т.е. возникает вторая ситуация, когда d_p>d₂ или 1,9180>1,36. С учетом этого мы можем сделать вывод: с вероятностью 0,95(95%) в ряде е_t отсутствует автокорреляция.

Проведя расчеты, можно сделать окончательный вывод, что выбранный степенной тренд адекватен той тенденции, которая имеет место во временном ряде, а уравнение тождественно уравнению ε_t= у_t – tr_t .