2.5 Расчет параметров линейного тренда с помощью метода наименьших квадратов (мнк)
Рассчитаем параметры линейного тренда с помощью метода наименьших квадратов (МНК), который дает наименьшее отклонение фактических данных от тренда.
Чтобы найти
параметры линейного тренда
,
необходимо решить систему нормальных
уравнений:
.
Построим таблицу:
Таблица 6
|
t |
Y(t) |
t2 |
ty |
|
1 |
7,9 |
1 |
7,9 |
|
2 |
8,6 |
4 |
17,2 |
|
3 |
7,3 |
9 |
21,9 |
|
4 |
6,8 |
16 |
27,2 |
|
5 |
5,9 |
25 |
29,5 |
|
6 |
6,2 |
36 |
37,2 |
|
7 |
6,7 |
49 |
46,9 |
|
8 |
5,8 |
64 |
46,4 |
|
9 |
6,0 |
81 |
54 |
|
10 |
5,2 |
100 |
52 |
|
11 |
5,0 |
121 |
55 |
|
12 |
4,4 |
144 |
52,8 |
|
∑78 |
75,8 |
650 |
448 |
Найдем параметры а0 и а1:
;
В результате
расчетов линейный тренд
примет конкретный вид
.
Рисунок 4
На основе визуального анализа, линейный тренда соответствует ранее сделанному выводу по данным временного ряда с высокой степенью вероятности то, что временной ряд и линейный тренд имеет тенденцию к снижению.
Сравним параметры линейного тренда, вычисленные графическим методом а0=8,1 и а1 = -0,28 и методом МНК а0=8,35 и а1 = -0,31. Они достаточно близки.
2.6 Выбор нелинейного тренда
Далее необходимо выбрать нелинейную модель и рассчитать ее параметры. Параболический тренд не подходит т.к. нет резкого изменения направления тенденции. Гиперболический тренд тоже не подходит т.к. значение не приближается к определённому пределу. Итак, остается степенной или показательный тренд, степенной тренд используется тогда, когда темпы роста экономического показателя, в среднем, либо постепенно возрастают, либо постепенно убывают.
Для этого рассчитаем цепные темпы роста в таблице 7.
Таблица 7
-
t
Y(t)
Тр,%
1
7,9
-
2
8,6
108,86
3
7,3
84,88
4
6,8
93,15
5
5,9
86,76
6
6,2
105,08
7
6,7
108,06
8
5,8
85,57
9
6,0
103,45
10
5,2
86,67
11
5,0
96,15
12
4,4
88
Итого
75,8
Расчет цепных темпов роста показывает, что они относительно постоянны. Это позволяет предположить, что объем сбыта продукции может быть описан с помощью показательного тренда.
Расчет
параметров для показательного тренда
.
Параметры для показательного тренда непосредственно методом МНК найти невозможно, так как этот тип тренда нелинейный. Чтобы обойти этот сдерживающий момент, осуществим линеаризацию показательного тренда с помощью натурального логарифма. В результате логарифмирования исходная трендовая модель будет выглядеть следующим образом:
В линеаризированной модели показательного тренда параметрами будут lna0 и lna1. Их значения можно найти методом МНК, построив видоизмененную систему линейных уравнений :
В результате решения этой системы уравнений найдем параметры линеаризированной модели показательного тренда следующим образом:
Для расчетов составим следующую таблицу:
Таблица 7
-
t
yt
t²
lnyt
t*lnyt
1
7,9
1
2,066863
2,066863
2
8,6
4
2,151762
4,303524
3
7,3
9
1,987874
5,963622
4
6,8
16
1,916923
7,667692
5
5,9
25
1,774952
8,874760
6
6,2
36
1,824549
10,947294
7
6,7
49
1,902108
13,314756
8
5,8
64
1,757858
14,062864
9
6
81
1,791759
16,125831
10
5,2
100
1,648659
16,486590
11
5
121
1,609438
17,703818
12
4,4
144
1,481605
17,779260
78
75,8
650
21,914350
135,296874
После того как найдены параметры линеаризированной модели показательного тренда, параметры lna0 и lna1 необходимо пропотенцировать, т.е. найти антилогарифмы чисел lna0 и lna1. Таким образом, параметры показательного тренда будут равны:
В результате
расчетов параметров показательный
тренд будет иметь следующий конкретный
вид:
.
Построим график показательного тренда в соответствии с рисунком 5
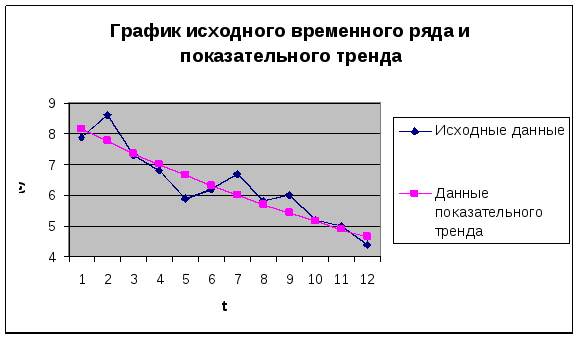
Рисунок 5
На основе визуального анализа видно: показательный тренд не совсем точно совпадает с реальным трендом временного ряда.