
2.6 Выбор передаточной функции датчика угла поворота
В качестве датчиков обратной связи принимаем индукционный двухотсчётный датчик угла ИПУ-ДУЦ. Индукционные двухотсчётные датчики угла класса синусно-косинусных вращающихся трансформаторов предназначены для применения в качестве двухотсчётных первичных преобразователей угла в цифровых системах "угол-параметр-код", а также в различных устройствах и системах дистанционной передачи угла. Конструктивно датчики выполнены двухфазными, без собственных подшипников и состоят из двух частей - статора и ротора, непосредственно встраиваемых в прибор.
Передаточная функция датчика обратной связи (индукционного двухотсчётного датчика угла) имеет вид:
![]() (23)
(23)
где kд – коэффициент усиления,
Tдос – электромеханическая постоянная датчика.
Коэффициент усиления kд можно определить по формуле Власова, по мощности:
![]() ,
(24)
,
(24)
где
![]() –
отклонение входной мощности,
–
отклонение входной мощности,
![]() – отклонение
выходной мощности редуктора.
– отклонение
выходной мощности редуктора.
Отклонение входной мощности датчика обратной связи относительно точки No по формуле Власова определяется в виде:
![]() (25)
(25)
где
![]() Вт. (26)
Вт. (26)
Отклонение выходной мощности датчика обратной связи относительно точки No определяется по формуле:
![]() (27)
(27)
где
![]() Вт. (28)
Вт. (28)
Коэффициент усиления в отклонениях по Власову, по мощности для датчика обратной связи определится в виде:
![]() .
(29)
.
(29)
Передаточная функция датчика обратной связи (индукционного двух отсчётного датчика угла) запишется в виде:
![]() .
(30)
.
(30)
3 РАСЧЕТ ДАТЧИКА ОБРАТНОЙ СВЯЗИ
Существует довольно большое количество датчиков угла поворота, разнообразной конструкции и видов. Выбор датчика обусловлен, прежде всего:
-
Физической природой регулируемого параметра.
-
Желаемой формой выходного сигнала (в данном случае желателен электрический выходной сигнал).
-
Высокой чувствительностью и чувствительностью.
-
Допустимой инерционностью.
-
Малым или отсутствием влияния внешних условий.
-
Возможностью настройки на различные значения регулируемого параметра.
-
Малой энергоемкостью.
-
Приемлемыми массогабаритные показателями.
-
Сроком службы.
В качестве датчиков обратной связи принимаем индукционный двухотсчётный датчик угла ИПУ-ДУЦ. Индукционные двухотсчётные датчики угла класса синусно-косинусных вращающихся трансформаторов предназначены для применения в качестве двухотсчётных первичных преобразователей угла в цифровых системах "угол-параметр-код", а также в различных устройствах и системах дистанционной передачи угла. Конструктивно датчики выполнены двухфазными, без собственных подшипников и состоят из двух частей - статора и ротора, непосредственно встраиваемых в прибор. Датчики выполняются из двух самостоятельных датчиков: грубого (ИПУ-ГО) и точного отсчёта (ИПУ-ТО).
Датчик ИПУ-ГО является двухполюсным классическим вращающимся трансформатором с синусоидально распределенными обмотками на роторе и статоре (по две квадратурных на каждом). Датчик ИПУ-ТО является многополюсным вращающимся трансформатором с сосредоточенными волновыми обмотками на сплошных магнитопроводах (на статоре - две квадратурные обмотки, на роторе - одна обмотка возбуждения). Конструктивно датчики выполняются аналогично асинхронным двигателям. Датчик выпускается совестно в комплекте с микропроцессорным комплексом (унифицированным цифровым вычислителем), полностью согласуется с выходным валом привода по угловой скорости, диаметру вала, частоте вращения вала, по степени защищенности, требуемому выходному сигналу, скорости изменения выходного сигнала.
Технические характеристики ИПУ-ДУЦ
Номинальное напряжение питания, В 6
Пусковой момент, не менее, Нм 0,35
Диапазон напряжения питания, В 6-12
Электромеханическая постоянная датчика, сек 0,1
Диапазон частот питания, кГц 1-10
Номинальная частота напряжения питания, кГц 4
Коэффициент электрической редукции ИПУ-ТО 64
Погрешность преобразования угла, не более угл.секунд. +6,9
Потребляемый ток, А, не более 0,13
Максимальное выходное напряжение, В (ТО/ГО) 0,4/ 4
Остаточная ЭДС, мВ, не более (ТО/ГО) 10/30
Рассогласование электрических нулей, угл.минут. 15
Масса, кг, не более 0,7
Срок службы, лет, не менее 15
Передаточная функция углового двухотсчетного датчика имеет вид в соответствии с формулой (23). Расчет коэффициентов передаточной функции двухотсчетного датчика угла приведен в пункте 2.6, расчет основных коэффициентов проводится в соответствии с формулами (24) – (30).
Расчет датчика обратной связи сводится к расчету допустимой температуры нагрева обмотки, а также расчету некоторых геометрических характеристик [9].
Значение максимально-допустимой температуры обмотки:
![]() (31)
(31)
где y – максимально допустимое напряжение, y = 1 103 кг/см2,
к – материал каркаса, к = 2,810-6 1/0С,
E – модуль упругости, E = 1,66 106 кг/см2,
Допустимое значение перегрева обмотки:
![]()
где Q0 max – максимальная температура окружающей среды, Q0 max = 450 0С
Диаметр провода обмотки из условия нагрева его максимальным током:
![]() (32)
(32)
где к – коэффициент, который выбирается в пределах 0,5 1 и учитывает, что не вся поверхность провода охлаждается;
– материал провода (медь), = 0,54 Ом·мм2/м,
– коэффициент теплоотдачи, = 1,2510-3 Вт/см20С
Средняя длина витка обмотки:
![]() (33)
(33)
где R0 – сопротивление датчика, R0 = 700 Ом,
f = (1,05 1,15) = 1,1.
Диаметр провода обмотки с изоляцией
![]() (34)
(34)
Диаметр каркаса:
![]() (35)
(35)
4 РАСЧЕТ УСТОЙЧИВОСТИ СИСТЕМЫ
4.1 Проверка устойчивости непрерывной части
Сначала найдем передаточную функцию непрерывной части. К непрерывной части относятся все элементы системы кроме микропроцессора.
Передаточная функция разомкнутой системы:
![]() (36)
(36)
Получим численное значение
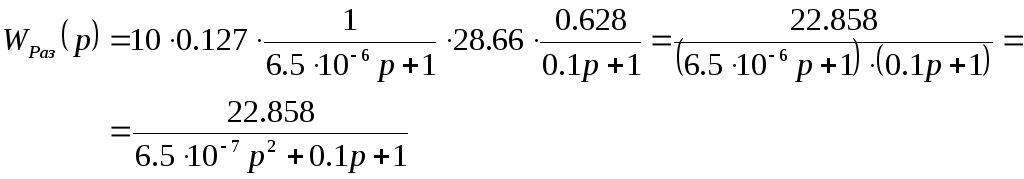
Проверим непрерывную часть на устойчивость. Проверку будем производить по критерию Гурвица. Для этого выпишем из передаточной функции системы характеристическое уравнение.
![]() (37)
(37)
Для того, чтобы САУ была устойчива необходимо и достаточно, чтобы все определители Гурвица были положительны.
Главный определитель Гурвица составляют по следующим правилам:
-
по главной диагонали записывают коэффициенты, начиная с а1 и заканчивая аn,
-
недостающие элементы столбца вверх заполняются коэффициентами с возрастающими индексами, а вниз с уменьшающимися,
-
если номер индекса i>n или i<0, то на месте такого элемента записывается ноль.
На основании выше изложенных правил составим определители Гурвица и вычислим их:
![]()
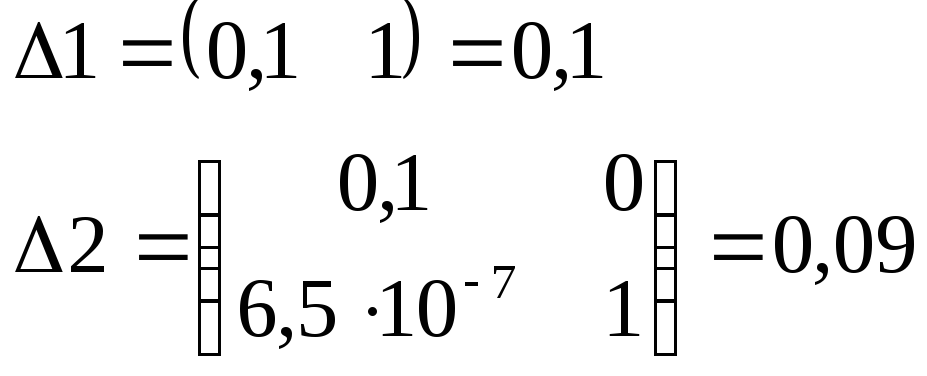
Как видно из расчетов непрерывная система устойчива, так как определители Гурвица положительны.
4.2 Проверка устойчивости системы с учетом микропроцессора
Для расчета устойчивости системы с учетом микропроцессора необходимо провести Z-преобразование замкнутой передаточной функции непрерывной части.
Передаточная функция замкнутой системы:
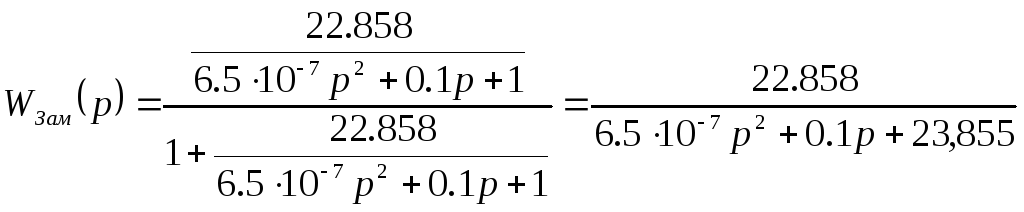 (38)
(38)
Разложим передаточную функцию WЗам(р) для облегчения z-преобразования
![]() (39)
(39)
Передаточная функция в форме z–преобразования имеет вид:
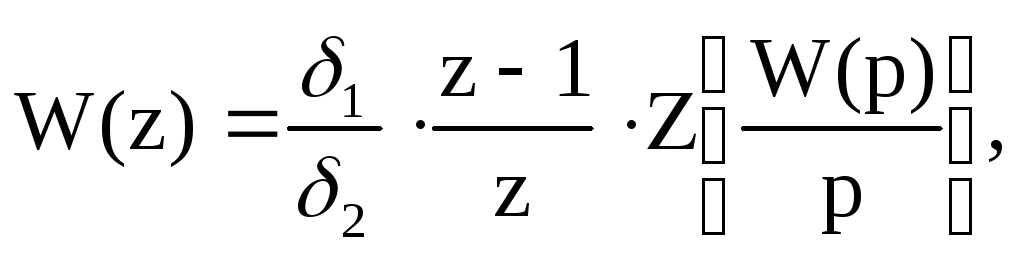 (40)
(40)
где δ1, δ2 – цены разрядов АЦП и ЦАП;
W(р) – передаточная функция системы;
(z-1)/z - фиксатор нулевого порядка.
Проведем z-преобразование каждой полученной простой дроби.
а)
![]()
![]()
![]()
![]()
![]()
где α – тактовая частота, α = 1,8·10-3;
То – период дискретности, То = 1,2.
Получим
![]() (41)
(41)
б)
![]()
![]()
![]()
![]()
![]()
Получим
![]() (42)
(42)
Z-преобразование обладает свойством линейности, для получения передаточной функции (39) умножим сумму найденных выше передаточных функций на фиксатор нулевого порядка (z-1)/z:
![]()
![]() (43)
(43)
Характеристическое уравнение передаточной функции замкнутой системы имеет вид:
![]() (44)
(44)
Преобразуем его, разделим обе части уравнения на 3,91
![]()
Из характеристического уравнения видно, что цифровая система автоматического регулирования устойчива.
4.3 Построение переходного процесса
Построим переходный процесс в системе. Для этого необходимо рассчитать передаточную функцию замкнутой системы, но так как она была рассчитана ранее воспользуемся соотношением (38). Получаем следующее выражение
![]()
Теперь произведем замену – переменную р заменим на переменную s, это необходимо для того чтобы выполнить обратное преобразование Лапласа.
![]()
По полученному выражению выполним обратное преобразование Лапласа с помощью программного пакета MathCAD v11.a Enterprise:
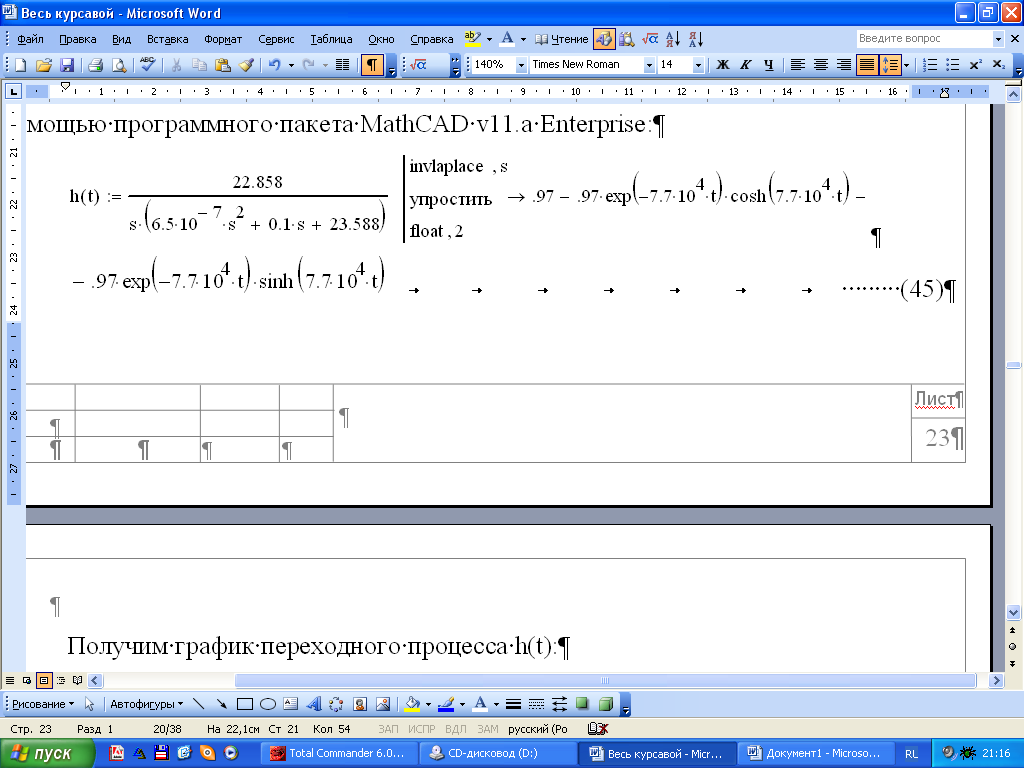
![]() (45)
(45)
П олучим
график переходного процесса h(t):
олучим
график переходного процесса h(t):
Рисунок 3 – График переходного процесса
4.4 Анализ качества управления СУ.
По полученному переходному процессу определяем следующие показатели качества управления СУ.
-
Установившееся значение по графику: hуст
 0.979
0.979
Тогда 5% интервал отклонения от установившегося значения будет соответствовать следующим величинам.
![]()
-
Время регулирования: tp=0,056 с.
-
Перерегулирование:
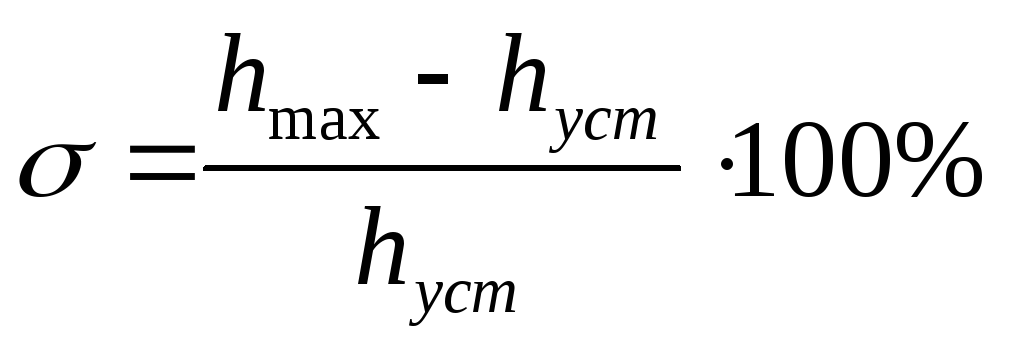
![]() по
графику будет равно
по
графику будет равно
![]() ,
тогда:
,
тогда:
![]()
-
Декремент затухания
![]()
![]()
![]()
-
Время достижения первого максимума: tmax=0,0046 c.
-
Время нарастания: tн=0,0025с.
-
Число колебаний за время регулирования: n=6.
-
Период колебаний: Т=0,0093 с.
-
Частота колебаний:

С учетом этих показателей можно сделать вывод, что качество управления СУ не соответствует требованиям нашей системы и требует дополнительной коррекции, так как перерегулирование и время регулирования слишком большие, а декремент затухания не достаточно велик, то примем значения выбранные нами при проектировании системы. Добиться улучшения переходной характеристики СУ можно путем введения дополнительных корректирующих звеньев.
5 ПОСТРОЕНИЕ ЛАЧХ И ЛФЧХ И ИХ АНАЛИЗ
5.1 Построение ЛАЧХ
Построение ЛАЧХ системы проводится асимптотическим методом. Асимптота – прямая линия с соответствующим наклоном. Длина асимптот ограничивается значениями частот сопряжения, которые определяются соответствующими звеньями.
Для построения ЛАЧХ воспользуемся передаточной функцией разомкнутой системы в форме Z-преобразования в зависимости от псевдочастоты .
![]() (46)
(46)
Проведем z-преобразование каждой полученной простой дроби по формуле (40), получим.
а)
![]()
![]()
![]()
![]()
![]()
где α – тактовая частота, α = 1,8·10-3;
То – период дискретности, То = 1.2, получим
![]()
б)
![]()
![]()
![]()
![]()
![]() получим
получим
![]()
Так как Z-преобразование имеет свойство линейности, получим
![]()
![]()
Произведем
замены:
![]() ,
,
![]() ,
получим
,
получим
В результате получим передаточную функцию в виде:
![]() 47)
47)
Получили апериодическое звено второго порядка. Представим функцию W(iλ) в виде:
![]() ,
,
где
![]()
![]()
W3(p) = 20lg(22,5) = 27.
Рассмотрим звенья W1(iλ) и W2(iλ).
Расположим звенья в порядке возрастания частот сопряжения. При λ< 50 влиянием звена W1(i) можно пренебречь. Частотные характеристики в этой области определяются звеном W2(i).
Для построения ФЧХ используем зависимость:
![]() . (48)
. (48)
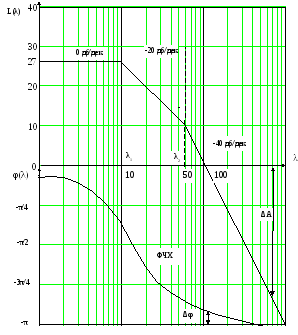
Рисунок 4 – Построение ЛАЧХ и ФЧХ
Анализ полученных графиков.
-
Полоса пропускания: λ = 1…105 с-1.
-
Запас устойчивости по фазе: Δφ = 200.
Запас устойчивости по амплитуде: ΔА = 28 дб.
6 ПОСТРОЕНИЕ И АНАЛИЗ ЖЕЛАЕМОЙ ЛАЧХ СИСТЕМЫ
Согласно техническим данным скорректированная САУ должна иметь следующие показатели качества.
Перерегулирование δ, % 30
Время регулирования t, с 20
Максимальная скорость g/, рад/с 20
Максимальное ускорение g//, рад/с 100
ЖЛАЧХ необходимо строить методом запретной зоны. Для определения запретной зоны построим АЧХ.

2
4
6
8
Рисунок 5 – АЧХ системы
Аmax = 3,2; Lmax = 20lg3,2=10. (49)
Критическая псевдочастота
![]() , (50)
, (50)
где g/ – скорость прохождения сигнала, рад/с;
g/ = Аλкcosλк; (51)
g// – ускорение прошедшего сигнала, рад/с;
g// = Аλк2 sinλк. (52)
Критическая псевдочастота λк = 2 с-1. Из технического задания: tрег = 20 с; δ = 30%. Частота среза λср = 3π/ tрег = 0,47. На графике точка λср входит в запретную зону, поэтому ЖЛАЧХ необходимо строить из точки λ/ср. Через точку λ/ср проводится наклон -20 дб/дек. Практика показала, что именно такой наклон обеспечивает простейший путь для получения ЖЛАЧХ. Эту асимптоту называют среднечастотной для Lж. Именно она определяет основные динамические свойства, которые связаны с длиной этой асимптоты. Для определения длины используется номограмма Солодовникова. На этой номограмме показана зависимость требуемых запасов устойчивости по амплитуде и фазе. Lm = 20. По найденному значению Lm на график наносятся 2 прямые Lm = const и - Lm = const. Они пересекают среднечастотную асимптоту Lж в точках а и b. Выделенный отрезок ab является искомым. Сопряжение среднечастотной асимптоты с высокочастотной и низкочастотной областями выполняется сопрягающей асимптотой с наклоном – 40дб/дек. Полученная Lж соответствует проектируемой системе.
ЖЛАЧХ и ЛАЧХ корректирующего устройства представлены на рисунке 6.
