2. Отступление на тему языка с. Бинарные операции.

В языке С есть возможность стандартной работы с битами, в рамках возможностей, предоставляемых обычными ассемблерами. Для работы с битами используются следующие арифметические операции:

• арифметическое и: &

• арифметическое или: |

• арифметическое не: ~

• арифметическое исключающее или: ^

• сдвиг влево на k разрядов: <<k

• сдвиг вправо на k разрядов: >>k

С помощью этих операций можно осуществить базовые операции с битами:

k-ый бит целого числа i == 0? : (i&(1<<k))==0

Положить 1 в k-ый бит целого числа i : i|=(1<<k)

Положить 0 в k-ый бит целого числа i : i&=~(1<<k)

Присвоить l-ый бит целого числа j k-тому биту i :

i = ((j&(1<<l))==0) ? (i&(~(1<<k))) : (i|(1<<k))

3. Высота красно-черного дерева

Наводящим соображением на то, что в красно-черном дереве, состоящем из N вершин, высота h=(log₂N) , является следующий факт: в каждой ветви дерева не менее половины вершин – черные (т.к., по определению красно-черного дерева, вслед за красной вершиной всегда следует черная), с другой стороны: в каждой ветви находится равное количество черных вершин.

Назовем черной высотой дерева с корневой вершиной r максимальное количество черных вершин во всех ветвях, начинающихся в r и заканчивающихся в листьях, не считая саму вершину r. Будем обозначать ее hb(r). Верна следующая

Лемма. В красно-черном дереве с черной высотой hb количество внутренних вершин не менее 2^hb+1-1.

Доказательство. По индукции по высоте дерева (обычной). Если рассмотреть лист (фиктивную вершину), то для нее лемма верна.

Рассмотрим внутреннюю вершину x. Пусть hb(x)=h. Тогда если ее потомок p - черный, то высота hb(p)=h-1, а если – красный, то hb(p)=h. Т.о., по предположению индукции, в поддеревьях содержится не менее 2^h-1 вершин, а во всем дереве, соответственно, не менее 2^h-1 + 2^h-1 + 1=2^h+1-1.



Если обычная высота дерева равна h, то черная высота дерева будет не меньше h/2-1 и, по лемме, количество внутренних вершин в дереве

N  2^h/2-1.

Прологарифмировав неравенство, имеем:

log₂ (N+1)  h/2

2log₂ (N+1)  h

h  2log₂ (N+1)

Итак, учитывая, что для любого бинарного дерева h > log₂ N, получаем, что доказана следующая

Теорема. Для красно-черного дерева, имеющего N внутренних вершин, верна следующая оценка для его высоты

h=(log₂N),

или, более точно,

log₂ N < h  2log₂ (N+1).

4. Добавление элемента в красно-черное дерево

Новая вершина вставляется в красно-черное дерева в два этапа.

На первом этапе вершина вставляется, как в обычное дерево поиска. Новая вершина красится в красный цвет. Следует отметить, что, в реальности фиктивных вершин может вообще не быть. Их наличие может обозначаться соответствующими нулевыми указателями у родительских вершин.

Добавление красной вершины x не меняет баланса дерева по черным вершинам.

Т.к. потомки новой вершины – фиктивные, то они – черные, по определению, что соответствует определению красно-черного дерева.

Единственная проблема, которая может возникнуть, это то, что у вставленной красной вершины x может оказаться красный родитель. Требуется изменить дерево, чтобы решить эту проблему.

При преобразованиях дерева мы будем сохранять указанное свойство: у нас будет сохраняться балансировка по черным вершинам и единственная возможная проблема это – некоторая красная вершина x будет иметь красного родителя.

Итак, x->par – красная, то x->par->par – черная (т.к. единственная проблема – нестыковка x->par и x, с другой стороны, у красной вершины может быть только черный родитель).

Будем называть вершину x->par->par->next, где next это – left или right дядей вершины x, если x->par->par->next!= x->par.

Рассмотрим все возможные случаи.

1. Дядя вершины - x красный.

Перекрашиваем родителя, деда и дядю вершины x и рассматриваем в качестве вершины x ее деда: x=x->par->par.

Т.о. мы перенесли проблему выше по ветви дерева.

Осталось рассмотреть случаи, когда дядя вершины x - черный.

2. Дядя вершины - x черный, x – левый потомок x->par.

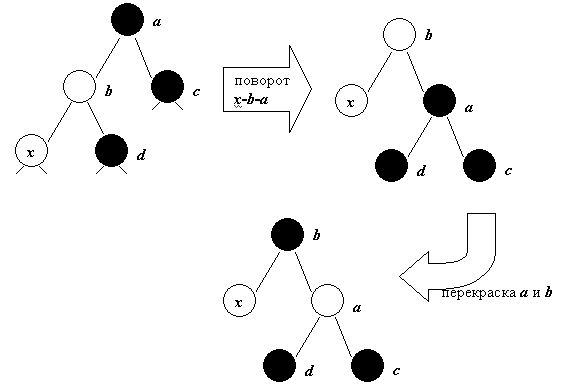
В этом случае мы проводим правый поворот x-b-a и в получившемся дереве перекрашиваем две вершины: a и b .

Вершина получившегося дерева – черная, проблем с цветами нет, баланс черного сохранился. Т.о. дерево сбалансировано. Последующая балансировка не требуется.

3. Дядя вершины - x черный, x – правый потомок x->par.

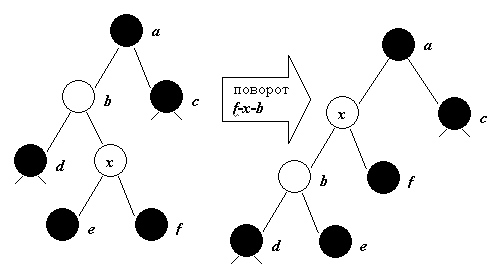
Делаем левый поворот f-x-b и ситуация сводится к предыдущему случаю.

4. У вершины x->par нет родителя, т.е. эта вершина – корневая. В таком случае мы просто перекрашиваем вершину x->par в черный цвет и процесс завершается.

Все случаи рассмотрены.

Итак, после добавления вершины процесс приведения дерева к виду красно-черного дерева сводится к некоторому количеству процедур перекраски 1 (не более h раз, где h – высота дерева) и не более чем к двум поворотам. Причем, после поворотов дерево не требует дальнейших изменений.

Итак, мы доказали следующую теорему

Теорема. Указанный алгоритм позволяет добавлять вершину к красно-черному дереву за время T=O(log₂N) операций, где N – количество вершин в дереве.