3.2.4. Вывод
Рассматриваемая АС неустойчивая, так как амплитудно-фазовая характеристика W (jw), разомкнутой системы находится на границе устойчивости, в точке с координатами (-1; j0).
3.3.
Для определения устойчивости системы
по критериям Гурвица и Михайлова
необходимо найти
характеристическое
уравнение для замкнутой системы. Ранее
была получена передаточная функция для
разомкнутой системы.
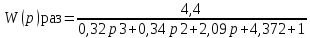
Для замкнутой АС с отрицательной обратной связью передаточная функция будет равна:
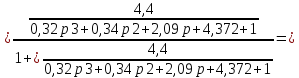
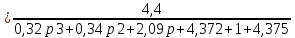
где знаменатель есть характеристическое уравнение для замкнутой АС, т.е.
G(p)=0,32р" + 0,34 р '+ 2,09 р + 5,375=0
3.3.1. Определим устойчивость по критерию Михайлова.
В характеристическое уравнение замкнутой АС вместо оператора р поставим значение jw, получим:
G(p)замк= 0,32р3 + 0,34 р2 + 2,09р + 5,375.
G(jw)замк =0,32(jw)3 + 0,34(jw)2 + 2,09(jw) + 5,375.
G(jw)замк = (5,375-0,34w2) +jw(2,09-0,32w2).
R(w) = 5,375 - 0,34w2 - действительная часть
J(w) = w(2,09 – 0,32w2) - мнимая часть.
Давая различные значения w в пределах w € (0,∞), найдем координаты R(w), J(w) точек годографа комплексного коэффициента передачи.
3.3.2. Вывод
Рассматриваемая АС неустойчива, т.к. годограф Михайлова не пересекает последовательно оси координат.
Таблица 2
Результаты
расчета
|
w |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
|
R(w) |
5,37 |
5,03 |
4,015 |
2,315 |
-0,065 |
-3,125 |
-6,866 |
|
J(w) |
0 |
1,77 |
1,62 |
-2,37 |
-12,12 |
-29,55 |
-56,56 |
|
7 |
8 |
9 |
10 |
11 |
12 |
|
-11,285 |
-16,38 |
-22,16 |
-28,62 |
-35,76 |
-43,58 |
|
-95,13 |
-147,12 |
-214,47 |
-299,1 |
-402,93 |
-527,88 |
|
13 |
14 |
15 |
|
-53,085 |
-61,265 |
-81,325 |
|
-675,87 |
-848,82 |
-1192,65 |
3.4. Определим устойчивость по критерию Гурвица.
Характеристическое
уравнение для замкнутой АС.
G(p) = 0,32p3+ 0,34 р2+ 2,09 р + 5,375
Составляем определитель из коэффициентов характеристического уравнения:
G(p) аор3 + a1p2 + а2р + а3 - общий вид уравнения
ао =0,32
где a1=0,34
а2=2,09
а3=5,375
ао<0; а1>=0,34; а2>0; а3>0.
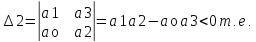
3.4.1.
Вывод. Коэффициенты
а0,
a1,
а2,
а3
отрицательный диагональный минор -
отрицательный
, следовательно рассматриваемая АС
неустойчива.
3.5. Определим устойчивость по критерию Вышнеградского
Этот критерий используется при определении устойчивости системы, для которой характеристическое уравнение имеет третий порядок.
В нашей системе характеристическое уравнение третьего порядка:
0,32p3+ 0,34 р2+ 2,09 р + 5,375=0
Уравнение необходимо преобразовать так, чтобы коэффициент при р3 был равен единице. Для этого разделим все члены характеристического уравнения па 0,32и получим:
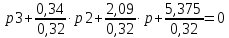
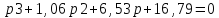
Где
С0=16,79
С1=6,53
С2=1,06
Находим величины
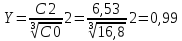
Получим:
Х .Y=0,41. 0,99=0,4< 0
3.5.1. Вывод. Произведение ХУ < 1, следовательно, АС неустойчива,