
курсовая работа / kursovaya_rabota_po_discipline_optimalnye_i_adaptivnye_siste
.docx
Министерство
образования и науки Российской Федерации
Федеральное агентство по образованию
Государственное образовательное учреждение высшего профессионального образования
САМАРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
Кафедра «Автоматика и управление в технических системах»
Курсовая работа по дисциплине
Оптимальные и адаптивные системы управления
Вариант 4
Проверил: Вохрышев В.Е.
Самара 2010
Содержание
2. Синтез оптимального управления методом АКАР 4
2.1. Синтез с использованием линейной агрегированной макропеременной 5
2.2. Синтез с использованием нелинейной агрегированной макропеременной 7
3. Моделирование системы в MathCAD 10
4. Заключение 16
5. Список литературы 17
Объект управления задан следующей передаточной функцией:
W(p)
=
 ;
;
Для выполняемого варианта курсовой работы параметры объекта имеют следующие значения:
T1 = 4; T2 = 1; T3 = 5; K = 5;
-
По заданной передаточной функции объекта синтезировать методом АКАР управление, выбрав в качестве агрегированной макропеременной линейную комбинацию фазовых координат.
-
Разработать цифровую модель системы в среде МСАD, исследовать систему методом цифрового моделирования, выполнить параметрическую оптимизацию управления.
-
Выполнить пункт 2 задания с учетом ограничений расходов на управление и фазовую координату Х4.
Для выполнения работы сначала выполнить все расчеты и моделирование, положив ψ в виде линейной комбинации фазовых координат, а φ(ψ)=ψ. В критерии принять m=c=1. Затем положить ψ=th(F(xi)+x4), i=1,3; F(xi)=k1x1+k2x2+x3, а φ(ψ)=ψ.
На фазовой плоскости совместить полученные графики при моделировании для двух случаев. Во временной области вывести управление и фазовые координаты, выполнив при необходимости их масштабирование. Провести анализ полученных результатов.
Граничные условия Х(0)=(20,0,0); Х(∞)=(0,0,0).
2. Синтез оптимального управления методом АКАР
Подставим заданные параметры в выражения для передаточной функции объекта управления:
W(p)
=
 =
=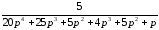 =
=
=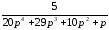 ;
;
Согласно определению передаточной функции, принимая за Y(p) изображение по Лапласу выходного сигнала, за U(p) - изображение по Лапласу входного сигнала, справедливо следующее выражение:
W(p)
= =
=
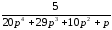 =>
=>
X(p)·( )
= 5U(p);
)
= 5U(p);
На
основе данного выражения получим
следующее дифференциальное уравнение:
20 +29
+29 + 10
+ 10 +
+
 = 5u(t);
= 5u(t);
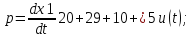
Представим данное дифференциальное уравнение в виде системы:
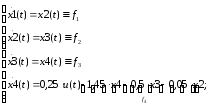
Критерий качества образуем при помощи следующего сопровождающего функционала:
J
=
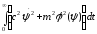 ;
;
В данном выражении ψ(x) –агрегированная макропеременная.
2.1. Синтез с использованием линейной агрегированной макропеременной
В выражении сопровождающего функционала вначале примем ψ(x) как линейную функцию:
ψ(x1, x2, x3, x4) = k1·x1 + k2·x2 + k3·x3 + x4;
Ее первая производная имеет следующий вид:
 =
k1·x2 + k2·x3 + k3·x4 + 0,25·u - 1,45·x4 - 0,5·x3 - 0,05·x2 =
=
k1·x2 + k2·x3 + k3·x4 + 0,25·u - 1,45·x4 - 0,5·x3 - 0,05·x2 =
=(k1 - 0,05)·x2 + (k2 - 0,5)·x3 + (k3 – 1,45)·x4+ 0,25·u ;
Примем φ(ψ)=ψ, c=m=1. Тогда после подстановки сопровождающий функционал примет следующий вид:
J= ;
;
Синтезируем закон оптимального по данному критерию управления. Для этого воспользуемся вторым универсальным соотношением метода АКАР:
U(t)
=
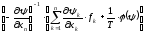 =
=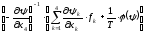 =
=
= ==
== ;
;
Полученный закон управления переводит объект из произвольного состояния в окрестность ψ=0. Получим теперь систему дифференциальных уравнений, описывающих движение изображающей точки вдоль ψ=0:
ψ=0= k1·x1 + k2·x2 + k3·x3 + x4 => x4 = - k1·x1 - k2·x2 - k3·x3;
Подставим данное выражение в первые (n-1) уравнений системы, описывающей объект управления. В результате получим:

Данную систему можно представить в виде одного дифференциального уравнения относительно x1ψ:
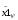 +
k3·
+
k3· +
k2·
+
k2· +
k1·
x1ψ
= 0; (*)
+
k1·
x1ψ
= 0; (*)
Для решения данного дифференциального уравнения составим следующее характеристическое уравнение:
λ 3 + k3· λ2 + k2· λ + k1 = 0;
Чтобы получить значения коэффициентов, при которых движение устойчиво, воспользуемся критерием устойчивости Гурвица. Определитель Гурвица в этом случае будет иметь следующий вид:
Δ
=![]() =
=
 ;
;
Согласно критерию Гурвица, для того, чтобы САУ была устойчива, необходимо и достаточно, чтобы все n диагональных миноров определителя Гурвица были положительны:
Δ1 =k3 > 0;
Δ2
=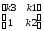 =
k3·k2 - 1·k1 > 0;
=
k3·k2 - 1·k1 > 0;
Δ3
= =0+0+k1·(k3·k2
- 1·k1) > 0;
=0+0+k1·(k3·k2
- 1·k1) > 0;
Обобщая полученные неравенства, получаем следующие условия для выбора значений коэффициентов характеристического уравнения:
k3 > 0; k2 > 0; k1 > 0; k3·k2 > k1;
Выберем теперь значения коэффициентов, удовлетворяющие данным условиям. Для удобства вычислений выберем коэффициенты так, чтобы можно было легко найти корни характеристического уравнения:
k1 = 1; k2 = 3; k3 = 3; =>
λ 3 + 3 λ2 + 3 λ + 1 = 0; => (λ + 1) 3 = 0; => λ1,2,3 = -1;
Общее решение дифференциального уравнения (*) имеет следующий вид:
x1(t) = C1·e λ1·t + C2·t·e λ2·t + C3·t 2 ·e λ3·t ;
Подставив в данное выражение полученные корни характеристического уравнения, получим:
x1(t) = C1·e -t + C2·t·e -t + C3·t 2 ·e -t ;
2.2. Синтез с использованием нелинейной агрегированной макропеременной
В выражении сопровождающего функционала теперь примем за ψ(x) функцию следующего вида:
ψ(x1, x2, x3, x4) = th(k1·x1 + k2·x2 + k3·x3) + x4;
Первая производная данной функции будет иметь следующий вид:
 =
=
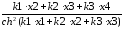 +
0,25·u
- 1,45·x4
- 0,5·x3
- 0,05·x2;
+
0,25·u
- 1,45·x4
- 0,5·x3
- 0,05·x2;
Примем φ(ψ)=ψ, c=m=1. Тогда после подстановки сопровождающий функционал примет следующий вид:
J= ;
;
Аналогично предыдущему расчету синтезируем закон оптимального по данному критерию управления:
U(t)
=
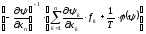 =
= =
=
=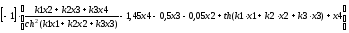 ==
== ;
;
Данный закон управления также переводит объект из произвольного состояния в окрестность ψ=0. Как и в предыдущем случае получим систему дифференциальных уравнений, описывающих движение изображающей точки вдоль ψ=0:
ψ=0= th(k1·x1 + k2·x2 + k3·x3) + x4 => x4 = - th(k1·x1 + k2·x2 + k3·x3);
Подставим данное выражение в первые (n-1) уравнений системы, описывающей объект управления:
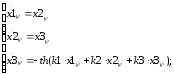
Представим данную систему в виде одного дифференциального уравнения относительно x1ψ:
 +
th(k3·
+
th(k3· +
k2·
+
k2·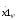 +
k1·
x1ψ
)= 0;
+
k1·
x1ψ
)= 0;
Однако в данном случае полученное уравнение нелинейно за счет функции гиперболического тангенса. Заменим эту функцию на ее приближенное значение и подставим в полученное дифференциальное уравнение:
th(x) ≈ x =>
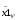 +
k3·
+
k3·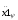 +
k2·
+
k2· +
k1·
x1ψ
= 0; (**)
+
k1·
x1ψ
= 0; (**)
Полученное в данном случае уравнение (**) представляет собой уравнение (*), полученное в предыдущем пункте. Следовательно, его решение так же соответствует решению уравнения (*):
x1(t) = C1·e -t + C2·t·e -t + C3·t 2 ·e -t ;
Произведем теперь моделирование заданной системы в MathCAD.
3. Моделирование системы в MathCAD
Реализация первого способа:


Рис.3.1
Реализация второго способа:
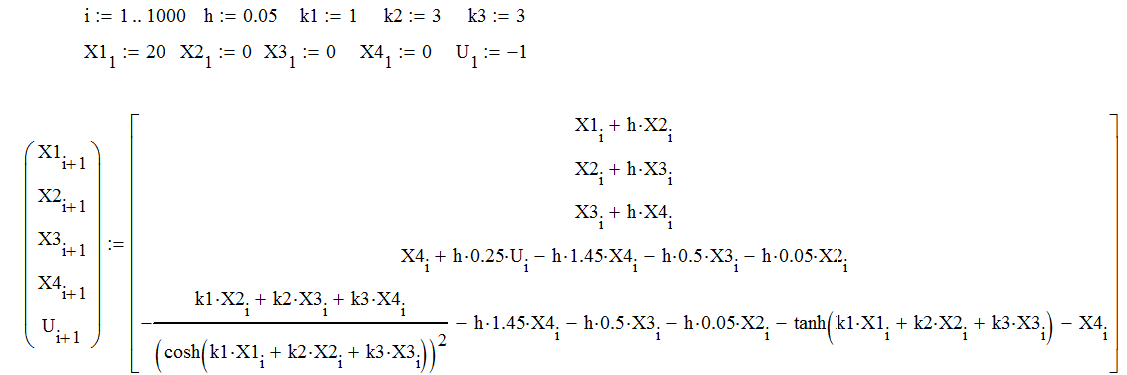
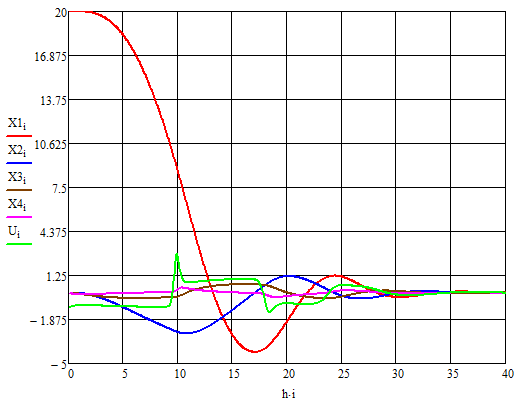
Рис.3.2
Сравнение полученных разными способами результатов:

Рис.3.3 Сравнение скорости изменения функции
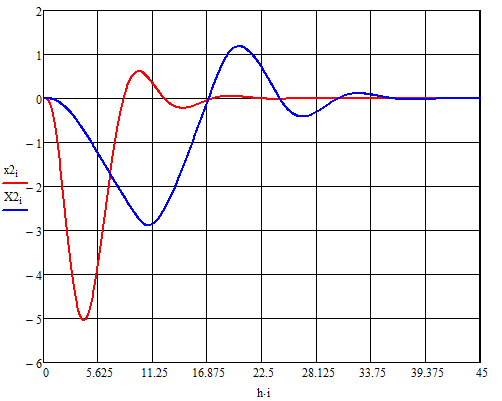
Рис.3.4 Сравнение изменения ускорения
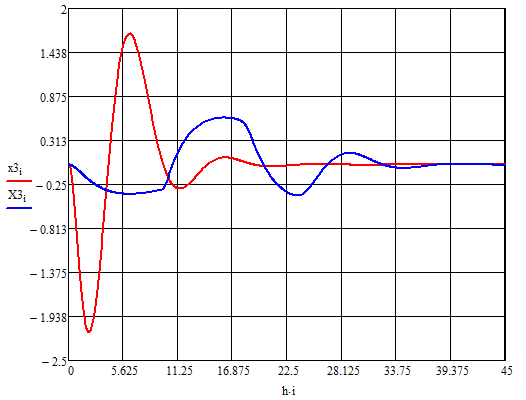
Рис.3.5 Сравнение изменения производной третьего порядка

Рис.3.6.
Сравнение изменения выходной координаты

Рис.3.7. Сравнение управляющих сигналов
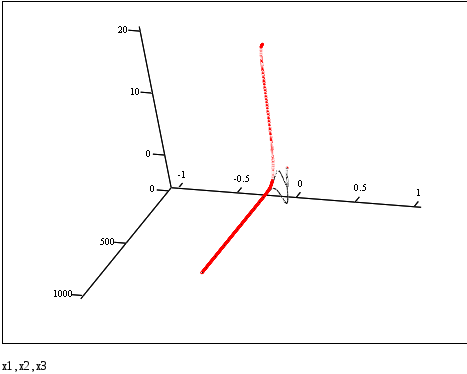
Рис 3.9
Рис 3.10
4. Заключение
При построении модели системы с использованием различных агрегированных макропеременных был выявлен наиболее эффективный способ оптимального по критерию наибольшего быстродействия управления.
Так управление, синтезированное с использованием линейной агрегированной макропеременной несколько быстрее приводит координаты в установившееся значение (см. рис 3.7), чем управление с использованием нелинейной макропеременной.
5. Список литературы
-
Колесников А.А. «Синергетическая теория управления»;
-
«Современная прикладная теория управления. Часть 2 – Синергетический подход» под ред. Колесникова А.А.
