3. Построение решения в Mathcad

3.1. Построение переходной и весовой функции

Построим переходную и весовую функцию искомой системы. Зададим коэффициенты передаточных функций:

Зададим структуру передаточных функций:

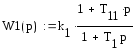
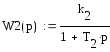
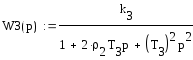
Построим переходную функцию блока W1(p), используя обратное преобразование Лапласа (рис.24):

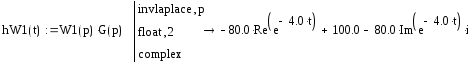
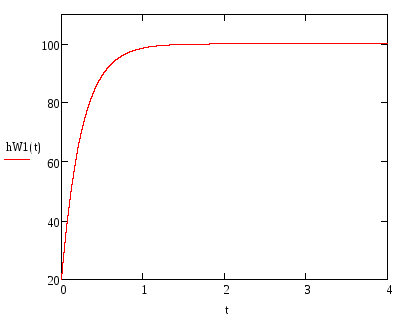
Рис.24. Переходная функция блока W1(p)

Построим переходную функцию блока W2(p), используя обратное преобразование Лапласа (рис.25):

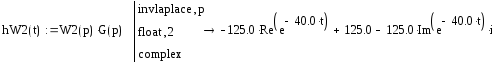
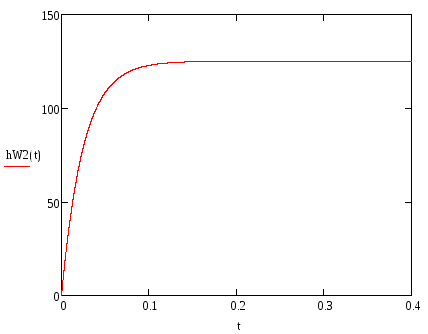
Рис.25. Переходная функция блока W1(p)

Построим переходную функцию блока W3(p), используя обратное преобразование Лапласа (рис.26):

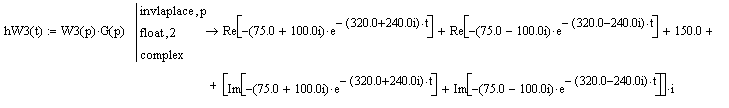
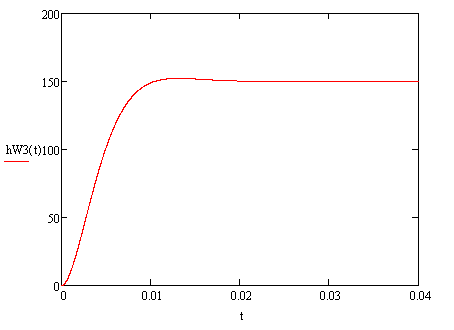
Рис.26. Переходная функция блока W3(p)

Так как у нас дано последовательное соединение передаточных функций, то общая передаточная функция исходной системы есть произведение данных передаточных функций.

Построим переходную функцию общей передаточной функции исходной системы, используя обратное преобразование Лапласа.

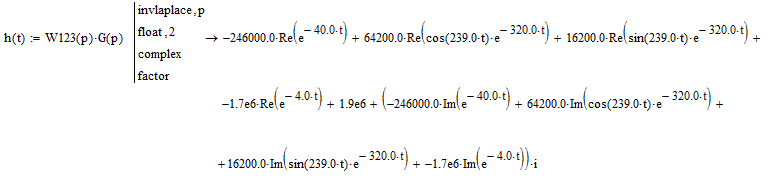
Получим график (рис.27):

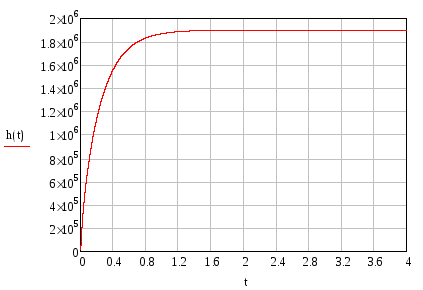
Рис. 27. Переходная функция исходной системы

Построим весовую функцию указанной системы, используя обратное преобразование Лапласа:

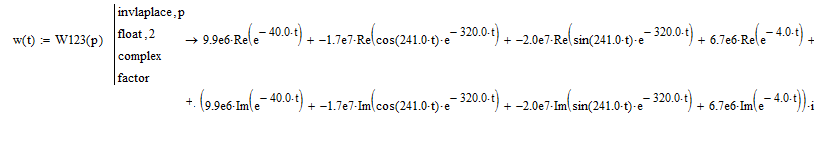
Получим график (рис.28) :

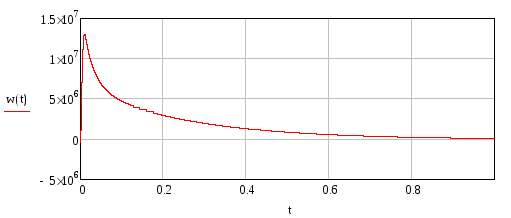
Рис.28. Весовая функция исходной системы

3.2. Анализ устойчивости

Исследуем на устойчивость систему с помощью матрицы Гурвица. Для этого построим и найдем 4 главных диагональных минора матрицы Гурвица, которая составлена из коэффициентов многочлена знаменателя.

Определяем коэффициенты знаменателя:

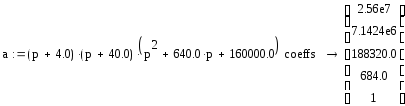
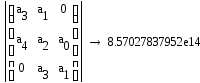
Проверяем устойчивость системы по критерию Гурвица:

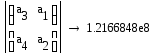
Все диагональные миноры положительны, следовательно, данная динамическая система устойчива.

3.3. Коррекция системы

Как видно, процесс имеет большую амплитуду. Внесем некоторые корректировки в исходную систему, чтоб уменьшить амплитуду:

Добавим усилительное звено с параметром k0=0.00001, тогда получим:

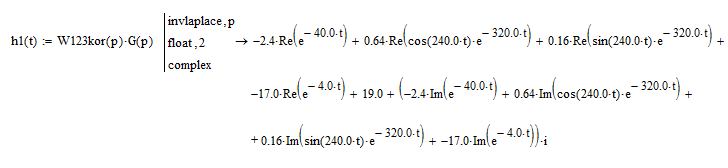
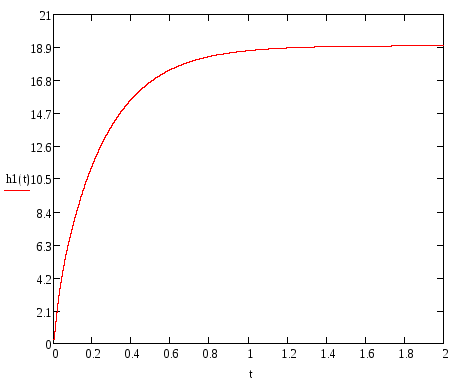
Рис. 29. Переходная функция корректированной системы

3.4. Перерегулирование

Итак, мы нашли перегулирование .

Время переходного процесса равно .

3.5. Нули и полюса системы

Найдем нули и полюсы системы:

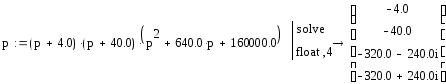
Система имеет нуль(z) и 4 комплексных полюса (p).

3.6. Частотные характеристики

Построим логарифмическую амплитудно-частотную характеристику (ЛАЧХ) и логарифмическую фазо-частотную характеристику новой системы (ЛФЧХ).

Асимптотические АЧХ звеньев

Построим графики ЛАЧХ данных звеньев:

Рис. 30. ЛАЧХ простейших составных звеньев

Составим сумму простейших составных звеньев, чтобы она наилучшим образом аппроксимировала имеющуюся ЛАЧХ новой системы.

Построение ЛAЧХ исходной разомкнутой системы

На графике представлены исходная и асимптотическая ЛАЧХ системы:

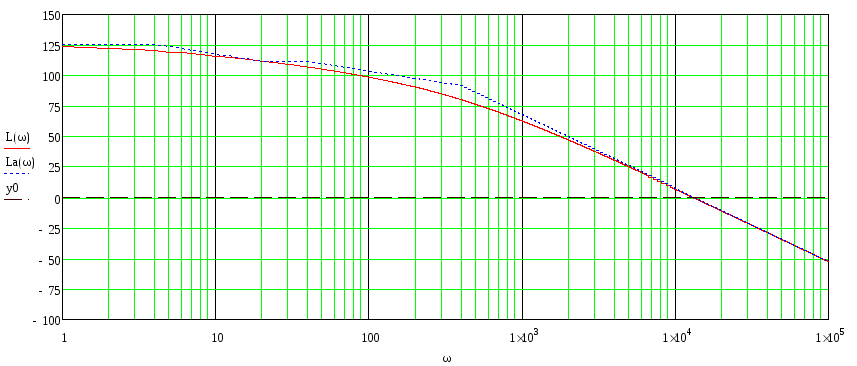
Рис 31. Исходная и асимптотическая ЛАЧХ системы

Построим логарифмическую фазо-частотную характеристику исходной системы (ЛФЧХ).

Получим график:

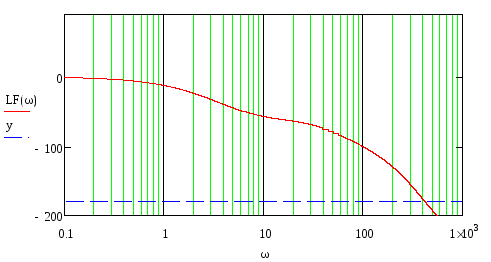
Рис.32. ЛФЧХ исходной системы

3.7. Построение желаемых частотных характеристик

Переход с низкочастотного участка на среднечастотный происходит на частоте w=796 rad/sec, а переход со среднечастотного участка на высокочастотный – на частоте 3960 rad/sec.

Учитывая, что перерегулирование должно быть меньше 30%, запас устойчивости порядка 15дБ, то можно получить передаточную функцию желаемой ЛАЧХ.

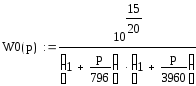
Построим временные характеристики полученной системы:

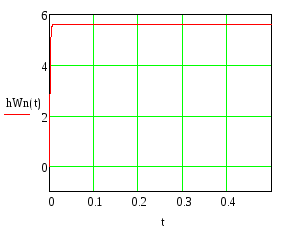
Рис.33. Переходная функция полученной системы

Рис. 34.Весовая функция полученной системы

Далее, построим логарифмическую амплитудно-частотную характеристику желаемой системы:

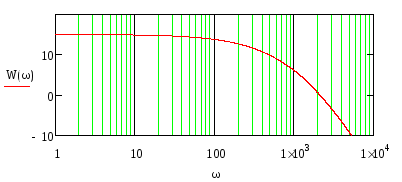
Рис. 35.ЛАЧХ желаемой системы.

Построим ЛФЧХ желаемой системы:

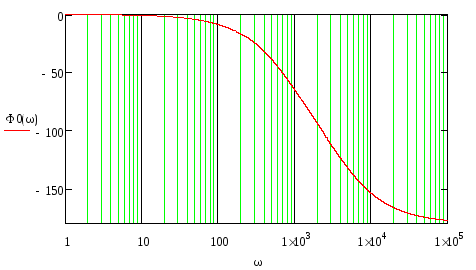
Рис. 36. ЛФЧХ желаемой системы.