3.3 Проведение z – преобразования

Для импульсных систем характерно построение решетчатых функций.

Для решетчатых функций времени может быть введено понятие дискретного преобразования Лапласа.

Для исследования импульсных систем большое распространение получило так называемое z-преобразование, которое связано с дискретным преобразованием Лапласа и вытекает из него.

Z-преобразование проведем по формуле:

(10)

где и - показатели цифрового преобразования. В рамках курсовой работы принимает их равными 1;

- передаточная функция импульсной системы.

Для начала разложим исходную общую передаточную функцию на простейшие дроби.

Для этого посчитаем корни знаменателя, разложим его на скобки.

Рассмотрим числитель отдельно:

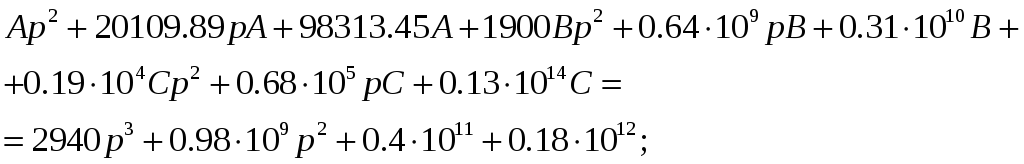
Вынесем общие множители за скобки:

Составим систему уравнений и найдем А, В, С:

Из первого уравнения системы найдем А:

Подставим во второе уравнение системы, получим В:

Оба уравнения подставим в третье уравнение системы и найдем С:

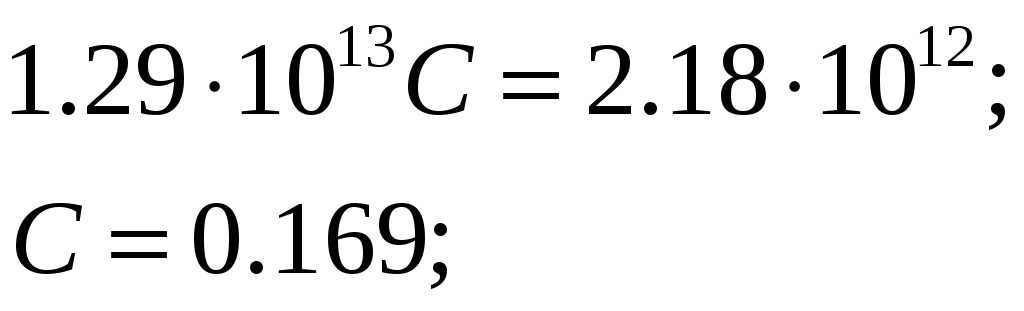
Таким образом:

Получили передаточную функцию выраженную через простейшие дроби:

Используя формулу (10) z- преобразования и формулу (10):

(11)

где Т₀=0,06, получим:

3.4 Определение устойчивости по Шур Кону

Определим устойчивость полученной импульсной системы по Шур Кону. Для устойчивости импульсной системы необходимо, чтобы коэффициенты характеристического уравнения были положительны:

В нашем случае характеристическое уравнение:

В характеристическом уравнении есть отрицательный коэффициент, следовательно, импульсная система не устойчива.

Проверим условия.

Составим определители Шур Кона.

;

;

;

Составим четвертый определитель Шур Кона:

Посчитаем нечетные миноры матрицы. Для того, что бы система была устойчивой, чтобы нечетные миноры матрицы Шур Кона были меньше нуля, либо четные миноры матрицы были больше нуля.

Посчитав миноры в MathCAD, получили, что, нечетные миноры положительны, а четные миноры отрицательны.

Таким образом, получаем, что импульсная система неустойчива.

Построим переходный процесс, используя программу MathCAD:

Рисунок 23 – Переходный процесс импульсной системы

Вывод:

Проанализировав переходный процесс, можно сказать, что импульсная система не устойчивая.

Заключение

В ходе данной курсовой работы, была рассмотрена система автоматического регулирования уровня жидкости в гидравлическом резервуаре. Были получены функциональная и структурная схемы системы. Исследована линейная, нелинейная и импульсная части системы.

В ходе исследования линейной части системы, была получена передаточная функция

, по которой был построен переходный процесс, который свидетельствовал об устойчивости линейной части системы ,и определены прямые оценки качества системы:

- установившееся состояние переходного процесса h_уст=1,4;

- 5% трубка;

- h_max=1.4;

- Время первого согласования t₁=0.25c;

- Время нарастания t_н=0.25c;

- Время регулирования t_р=0.125 c.

Была построена амплитудо - частотная характеристика системы и определены косвенные оценки качества:

- Амплитуда при нулевой частоте A(0)=1.428;

- Максимальная амплитуда А_max=1.428;

- Резонансная частота w_p=0 Гц;

- Частота среза, при которой амплитуда, равна 1 w_cp=29 Гц;

- Полоса пропускания: 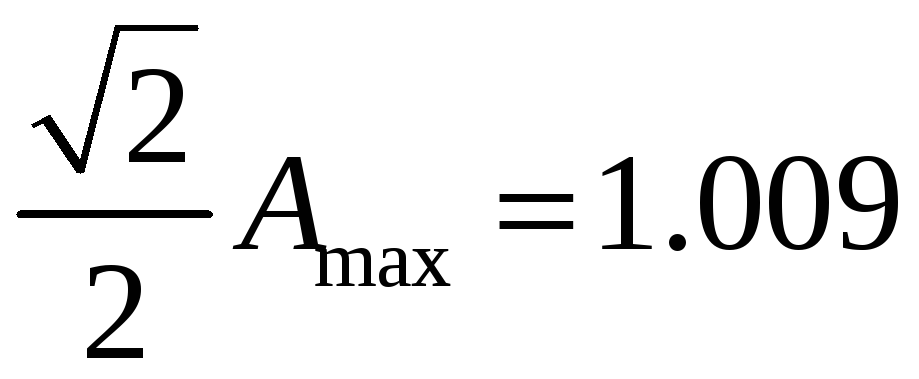w₂=28.16 Гц.

По критериям Гурвица и Найквиста определили, что линейная система устойчива.

В ходе исследования нелинейной части системы, с заданной статической характеристикой нелинейного элемента, был построен фазовый портрет - кривая с замкнутым циклом. Построен переходный процесс нелинейной системы, который свидетельствует об устойчивых автоколебаниях, амплитудой , и частотой . Включение нелинейного элемента в системы никак не отразилось на ее устойчивости.

В ходе исследования импульсной части системы, была получена общая передаточная функция:

.

Провели z –преобразование, и получили:

Построили переходный процесс, по которому можно сказать, что импульсная системы неустойчивая. Критерий Шур Кона показал, что импульсная система неустойчивая. Таким образом при введении импульсного элемента в систему, система становится неустойчивой.