2.2 Упрощение нелинейной системы.
По правилам преобразования структурных схем преобразуем нелинейную систему.
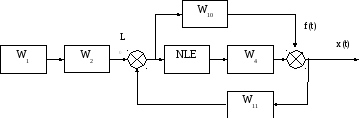
Рисунок 12 - Вид структурной схемы
Рисунок 13 - Вид структурной схемы
Приведем структурную схему к виду:
Рисунок 14 - Вид структурной схемы
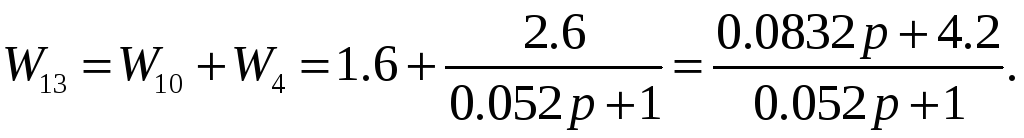
Рисунок 15 - Вид структурной схемы
Далее приведем систему к виду:
Рисунок 15 - Вид структурной схемы
Введем вынужденную обратную связь (рисунок 16):
Рисунок 16 - Вид структурной схемы
Передаточная функция линейной части запишется в виде:
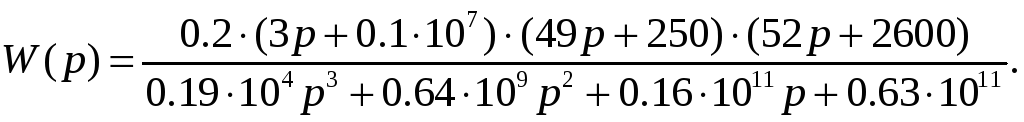
2.3 Построение фазового портрета
Передаточная
функция есть
или
,
(9)
где
-передаточная
функция линейной системы;
Подставляя в формулу (9) значение передаточной функции получим:
.
Приведенную формулу можно записать в виде:
Воспользуемся пакетом MathCad для решения этого дифференциального уравнения.
Введем
замену
и исключим из правой части уравнения
производную:
Для того чтобы построить фазовый портрет, необходимо, чтобы степень числителя и знаменателя не превышала вторую степень, поэтому элементы выше второй степени исключаем. Тогда получим:
Так
как в качестве нелинейного элемента
используется реле с гистерезисом со
статической характеристикой, представленной
на рисунке 11, то подставляя значение
для двух участков, получим систему:
Создадим матрицу для решения дифференциального уравнения.
В данной матрице реализовано условие перехода от одного уравнения к другому. Зададим матрицы для трех начальных условий:
Возьмем
количество точек равным 1000 и конечное
время интегрирования 200, то матрица
решений запишется как:
Построим фазовый портрет:
Рисунок 17 - Фазовый портрет нелинейной системы
Рисунок 18 – Переходный процесс
Вывод:
На
рисунке 17 представлен фазовый портрет
нелинейной системы. Это типовой вид
кривой. Переключение с одного уравнения
на другое происходит в точке
=
5, при
>0,
и в точке
=
-5, при
<0
. Характер фазовой линии такой, что она
стремится к устойчивому состоянию, о
чем свидетельствует автоколебательный
процесс (рисунок 18), и впоследствии
образует замкнутый цикл на фазовом
портрете.
Система производит автоколебания в предельном цикле с амплитудой:
,
и частотой
3 Исследование импульсной системы
3.1 Техническое задание
-
передаточная функция (ПФ) вентиля 10;
-
ПФ задатчика станции
управления 5;
- ПФ резервуара 4;
- ПФ ротаметра 5;
- ПФ вентиля 1;
-
ПФ дифманометра - уровнемера 9 прибора
6;
- ПФ регулятор комплекса 6;
-
ПФ манометра 8.
Рисунок 19 – Функциональная схема система
Из первоначальной линейной системы сделаем импульсную, для этого предположим, что передаточная функция первого элемента системы равна 1
3.2 Преобразование структурной схемы.
На рисунке 20 изображена структурная схема импульсной системы,
Численные значения передаточных функций:
W5
W6
f(t)
И
L0 x(t)
W1 W2
W3
W4
Lизм
W7
W9
W8
Пневмат.сигнал,
Р-давление Электрический
сигнал,
-
передаточная функция (ПФ) вентиля 10;
-
ПФ задатчика станции
управления 5;
- ПФ клапана 2;
- ПФ резервуара 4;
- ПФ ротаметра 5;
- ПФ вентиля 1;
-
ПФ дифманометра - уровнемера 9 прибора
6;
- ПФ регулятор комплекса 6;
-
ПФ манометра 8;
Рисунок 20 – Структурная схема импульсной системы
Применяя правила преобразования структурных схем, упростим нашу схему.
Преобразование структурной схемы:
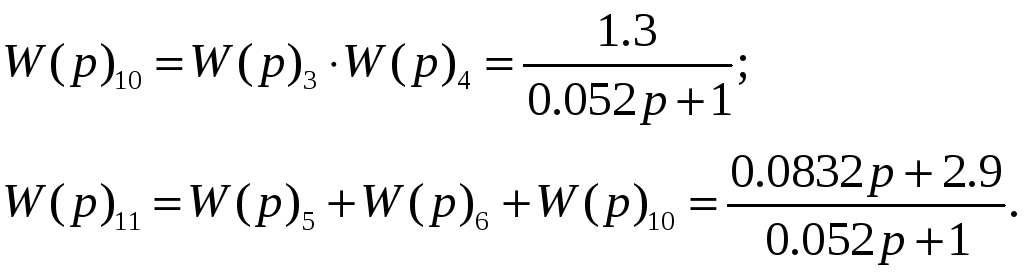
Рисунок 21 - Вид структурной схемы
Рисунок 22 - Вид структурной схемы
Преобразуем с учетом обратной связи:
Используя программу MathCAD, подставив значения функций:
получим выражение общей передаточной функции:
