3. Построение лачх и лфчх разомкнутой по внешнему контуру предлагаемой сау и определение запасов устойчивости сау.

После выбора регуляторов общая расчетная структурная схема САУ приобрела вид рис.16

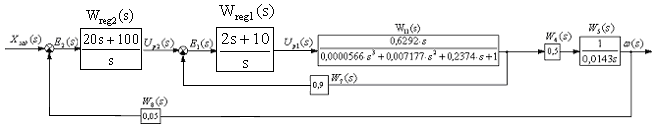
Рис.17 Эквивалентная расчетная схема САУ с выбранными регуляторами

Компьютерная программа CVG66-2 была составлена так, что позволяет решить поставленную задачу построения ЛЧХ разомкнутой САУ по внешнему контуру и оценки устойчивости замкнутой системы.

При конкретной работе с программой рекомендуется контролировать промежуточные данные, что достигается путем снятия символа ; и новым прогонам программы.

В результате были выведены расчетно-точные ЛАЧХ ЛФЧХ разомкнутой системы по внешнему контуру рис.17:

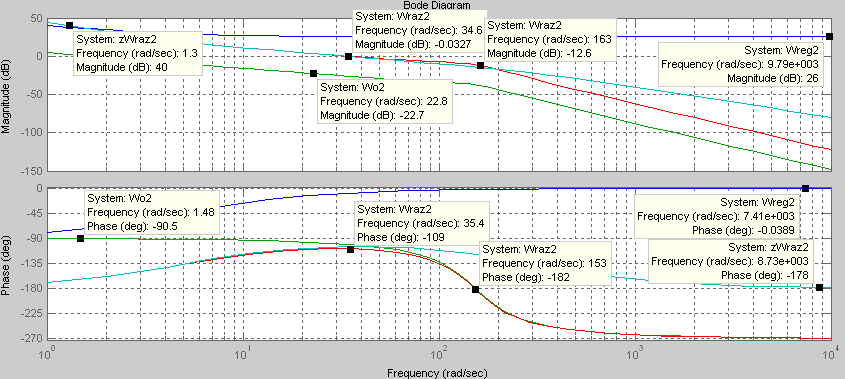
Рис.18 ЛАЧХ и ЛФЧХ внешнего контура САУ расчетной системы.

Анализ характеристик рис.17 показывает, что , используя номограммы [1 стр.488] можно оценочно оценить время переходного процесса (при). Сдвиг по фазе приравен. Запас по фазе будет, а запас по амплитуде. То естьсистема получится устойчивой с приемлемыми запасами устойчивости.

Программа CVG66-2 позволила найти и переходные функции замкнутой САУ при разных методах точности расчета рис.17.

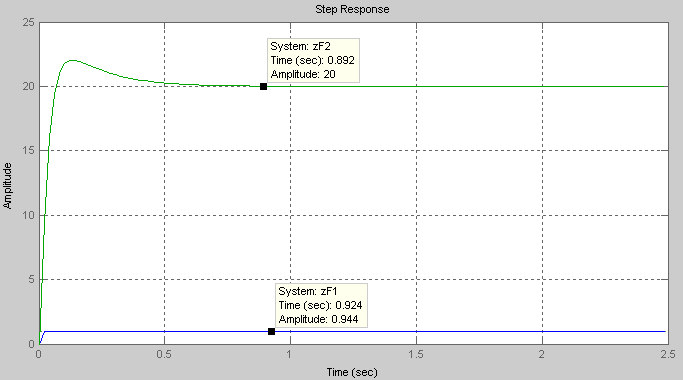
Рис.19 Переходные функции элементов внешнего контура упрощенной САУ

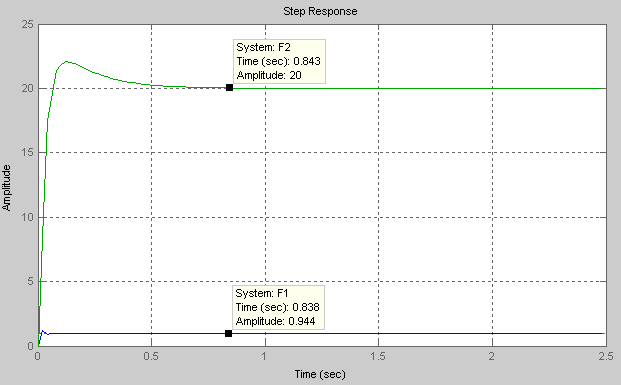
Рис.20 Переходные функции элементов внешнего контура расчетной САУ

Из рис.18 видно, что ожидаемое время переходного процесса около 0,8 с. Итоговые переходные процессы примерно одинаковые, хотя в первом случае были упрощения передаточной функции объекта до .

4. Передаточные функции и дифференциальные уравнения замкнутой сау

После выбора регуляторов и проверки на устойчивость замкнутой САУ по ЛЧХ разомкнутой системы (2-й пункт работы) общая структурная схема САУ приобрела вид рис.19.

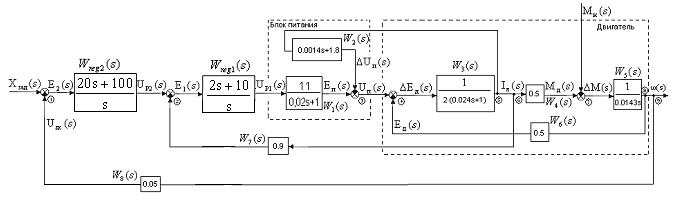
Рис.21

Прежде чем будем находить требуемые передаточные функции:

а) ; б); в)(9)

замкнутой системы рис.21 сделаем ряд структурных преобразований облегчающих решение поставленных задач. Ряд преобразований мы уже проделывали раньше, но только для усеченной системы (считали Сейчас же начнем с эквивалентных преобразований средней части структурной схемы рис.19.

Перенесем эквивалентно сумматор 3 через сумматор 4 по направлению распространения сигнала и получим эквивалентную структурную схему рис.20

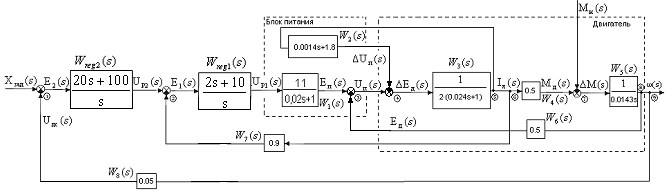
Рис.22 Эквивалентная структурная схема САУ.

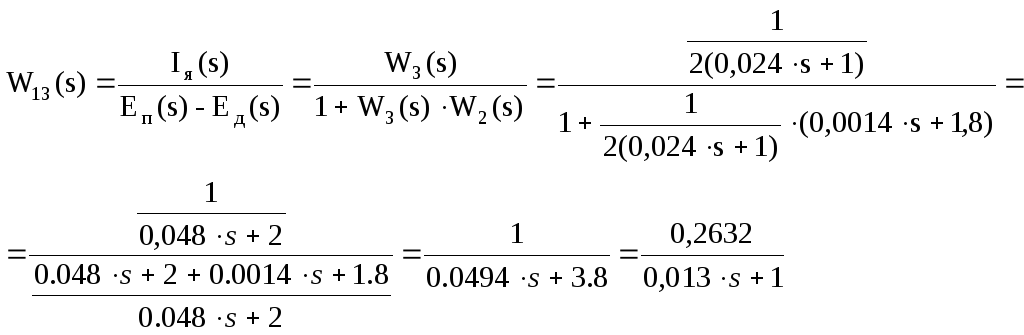(10)

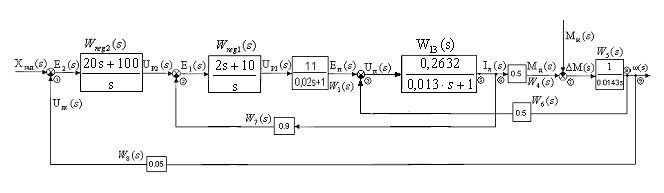
Рис.23 Эквивалентная структурная схема САУ.

Затем перенесем сумматор 2 последовательно в направлении распространения сигнала через звено затем через звено, а затем через сумматор 4 эквивалентно и получим эквивалентную структурную схему рис.22.

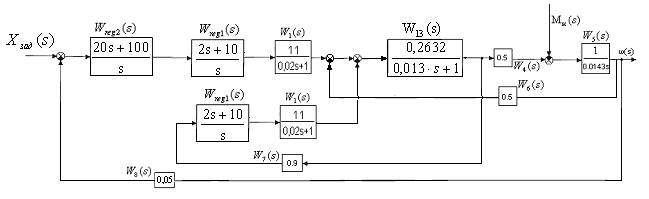
Рис.24 Эквивалентная структурная схема САУ.

В эквивалентной структурной схеме САУ рис.22 видно, что звено охвачено отрицательной обратной связью, где в обратной связи последовательно включены звенья,,. Соответственно их эквивалентная передаточная функциябудет:

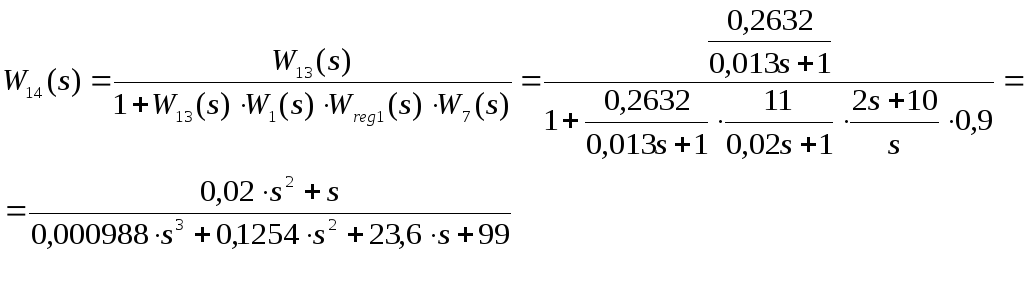
(11)

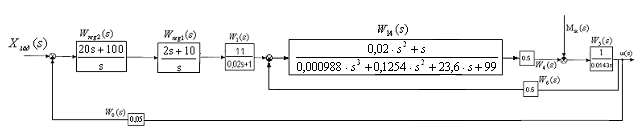
Рис.25 Эквивалентная структурная схема САУ.

Звенья ,,соединены последовательно, и их эквивалентная передаточная функциябудет равна:

(12)

Также звенья ,соединены последовательно, и их передаточная функциябудет равна:

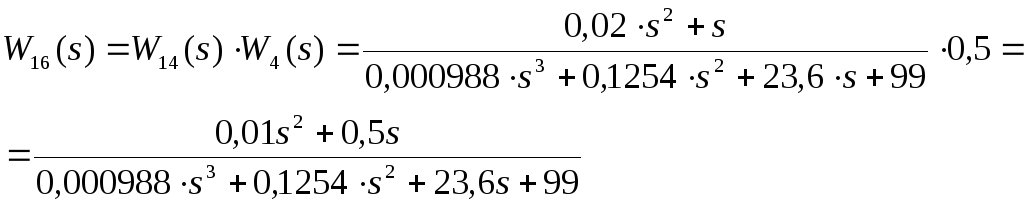(13)

Рис.26 Эквивалентная структурная схема САУ.

Полученная эквивалентная структурная схема рис.24 значительно упрощает нахождение требуемых передаточных функций и дифференциальных уравнений замкнутой САУ.

А) Главная передаточная функция .

Согласно определения о передаточной функции расчетная структурная схема рис.24 может быть представлена рис.25.

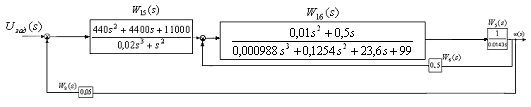
Рис.27 Структурная схема для определения .

Заменим часть схемы рис.27 с передаточными функциями ,иэквивалентной передаточной функцией:

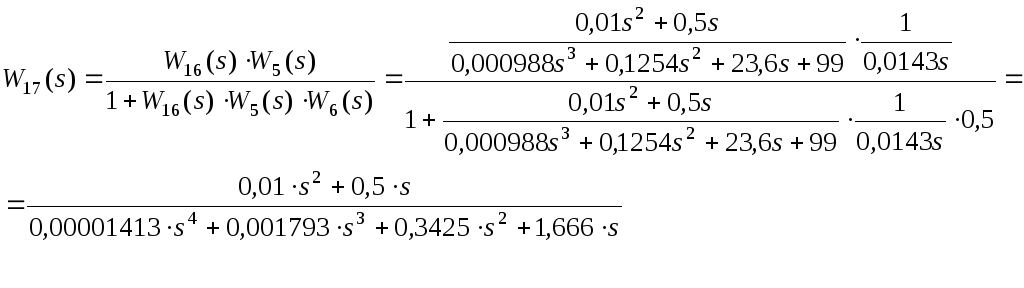
(14)

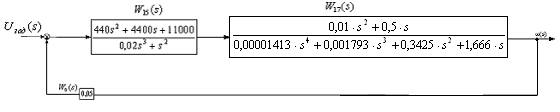
Рис.28 Структурная схема для определения на втором шаге.

Рассматривая рис.28 видим, что:

(15)

Используя (17) записал соответствующее дифференциальное уравнение (18):

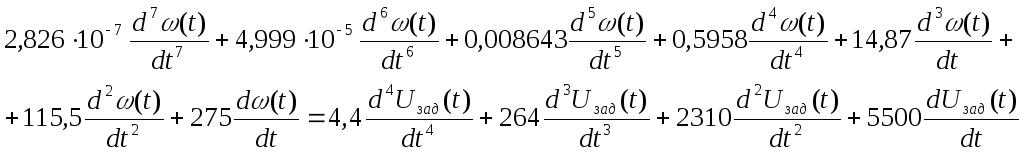
(16)

Б) Передаточная функция замкнутой системы для управляемой величиныпо нагрузкеможет быть получена, если в рис.26 принять. Согласно определения о передаточной функции расчетная схема рис.26 примет вид рис.29

Рис.29 Структурная схема для определения .

Звенья , (-),включены последовательно введем для них передаточную функцию:

(17)

Звенья ивключены параллельно, найдем их передаточную функцию:

(18)

Соответственно расчетную схему рис.29 можно представить эквивалентным рис.30.

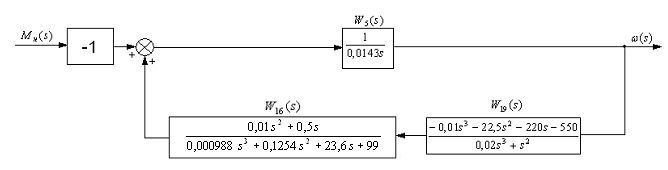
Рис.30 Структурная схема для определения второй шаг.

Соответственно передаточная функция замкнутой системы для управляемой величины по нагрузкебудет:

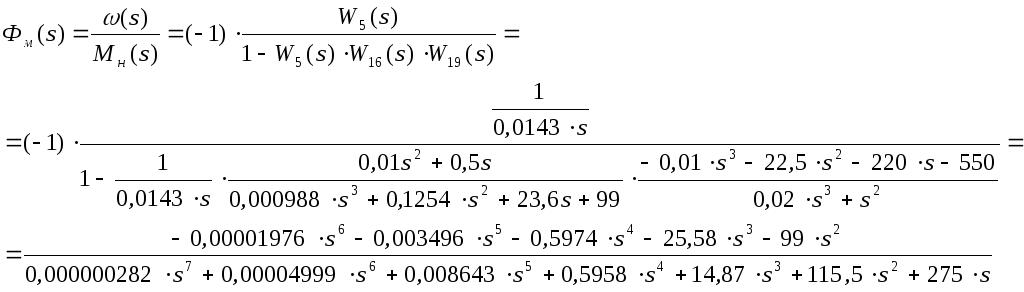(19)

Используя (19) записал соответствующее дифференциальное уравнение (20):

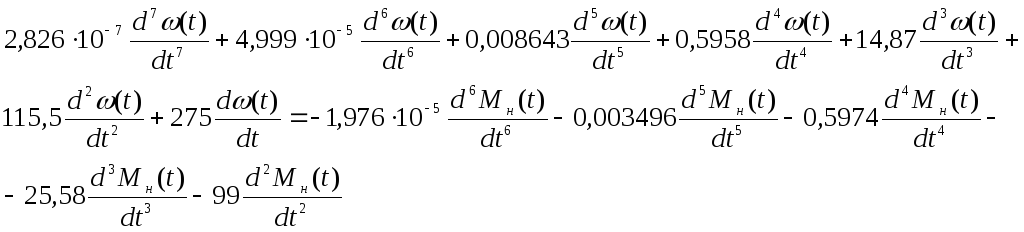
(20)

В) Передаточная функция замкнутой системы для токапо нагрузке задающему воздействиюможет быть получена, если в рис.25 принять. Согласно определения о передаточной функции расчетная схема рис.26 примет вид рис.31.

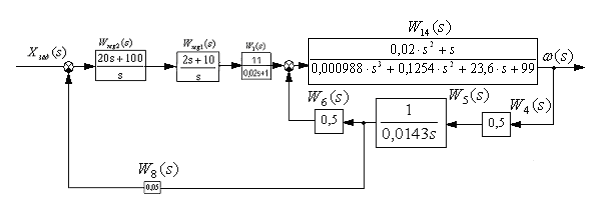
Рис31 Структурная схема для определения .

Произведем еще одно эквивалентное структурное преобразование и получим рис.32.

Рис.32 Структурная схема для определения , второй шаг.

На структурной схеме рис.30 видно, что звено охвачено отрицательной обратной связью, где в обратной связи три последовательно включенных звена,,. Введем для этой части передаточную функциюи получим:

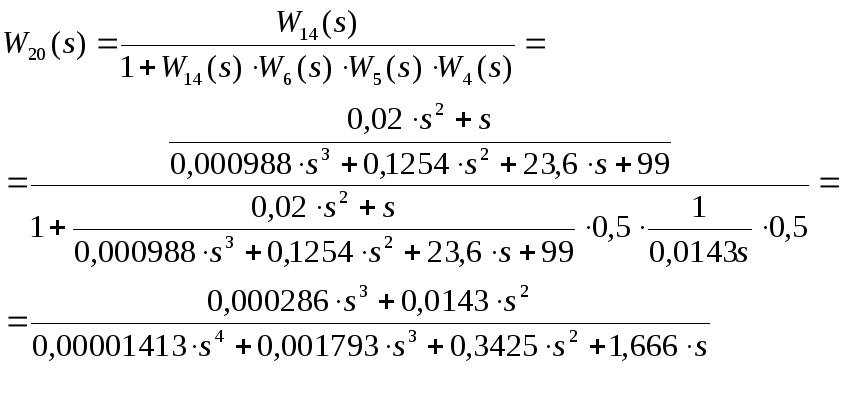(21)

А структурная схема рис.32 приобретет вид рис.33:

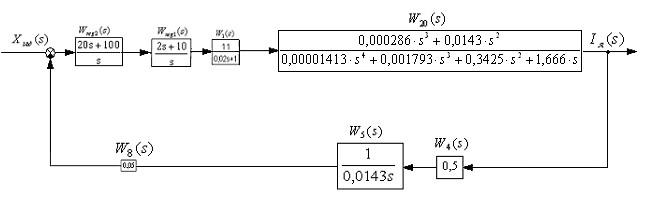
Рис.33 Структурная схема для определения , третий шаг.

Соответственно передаточная функция замкнутой системы для токапо задающему напряжениюбудет:

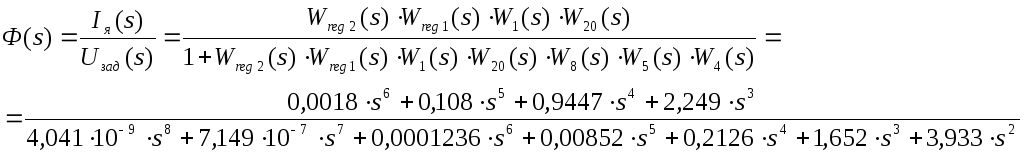
(22)

Используя (22) записал соответствующее дифференциальное уравнение (23):

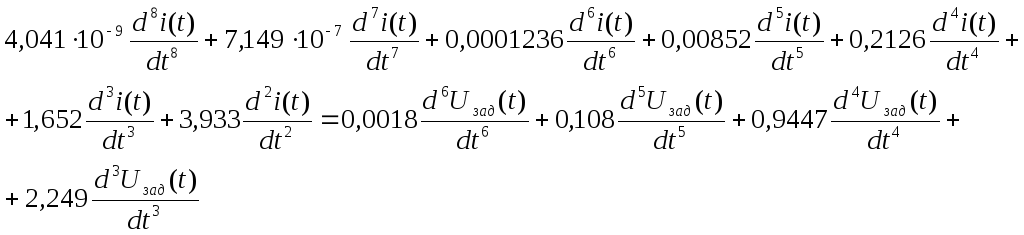
(23)