Содержание

Введение……………………………………………………………….....3

1 Постановка задачи………………………………………………..4

2 Структурная схема системы……………………………………..5

3 Динамические характеристики линейной системы…………...12

4 Исследование устойчивости исходной системы……………....22

5 Коррекция динамических характеристик системы…………...24

6 Анализ устойчивости скорректированной системы…………..27

Заключение…………………………………………………………..…30

Список использованных источников....................................................31

Введение

В настоящее время почти во всех областях народного хозяйства значительную роль в повышении уровня производства играет автоматизация различного рода процессов. Развитие автоматического управления как одной из базовых наук и реализация научных результатов, обуславливающих рациональные технико-экономические решения, являются главными условиями совершенствования автоматических систем.

Современные методы расчета систем автоматического управления (САУ) позволяют получить структуры и параметры систем, обеспечивающие высокую точность отработки заданных законов движения, и учесть при этом различного рода возмущения, дискретность и нелинейность устройств и т.д. Развитие теории оптимального управления привело к возможности построения систем, обладающих наилучшими в каком-либо смысле показателями их функционирования, характеризуемыми такими критериальными оценками, как быстродействие, минимумы расхода энергии, затрат ресурсов и др.

курсовая работа посвящена анализу и синтезу линейной САУ, что включает в себя построение структурной схемы, нахождение основных динамических характеристик системы, ее исследование на устойчивость с помощью заданного критерия, а также последующую коррекцию характеристик системы и проверку устойчивости скорректированной системы.

Для математических расчетов и моделирования (в том числе визуального) линейной системы управления, в курсовой работе используется рабочая среда MatLab. Она представляет собой хорошо опробованную и надежную систему компьютерной математики (СКМ), рассчитанную на решение самого широкого круга математических задач.

1 Постановка задачи

Известна модель объекта в виде системы дифференциальных уравнений:

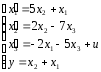
где x₁ – входной сигнал, y – выходной сигнал.

Произвести анализ и синтез данной модели управления. Для анализа устойчивости использовать критерий Найквиста.

2 Структурная схема системы

Структурная схема, построена с помощью пакета прикладных программ Simulink системы MatLab 6.5. Для построения структурной схемы использовались такие элементы как: 3 интегратора (Integrator), 5 усилителей (Gain), 5 сумматоров, источник сигналов возмущающих воздействий (Step) и осциллограф (Scope) для наблюдения результатов моделирования. Структурная схема системы представлена на рисунке 2.1.

Рисунок 2.1 – Структурная схема системы

Данную структурную схему можно привести к более простому виду, с помощью правил структурных преобразований. Части структурной схемы, изображённые на рисунке 2.2, могут быть заменены четырьмя блоками, с передаточными функциями W₁(s),W₂(s) и W₃(s).

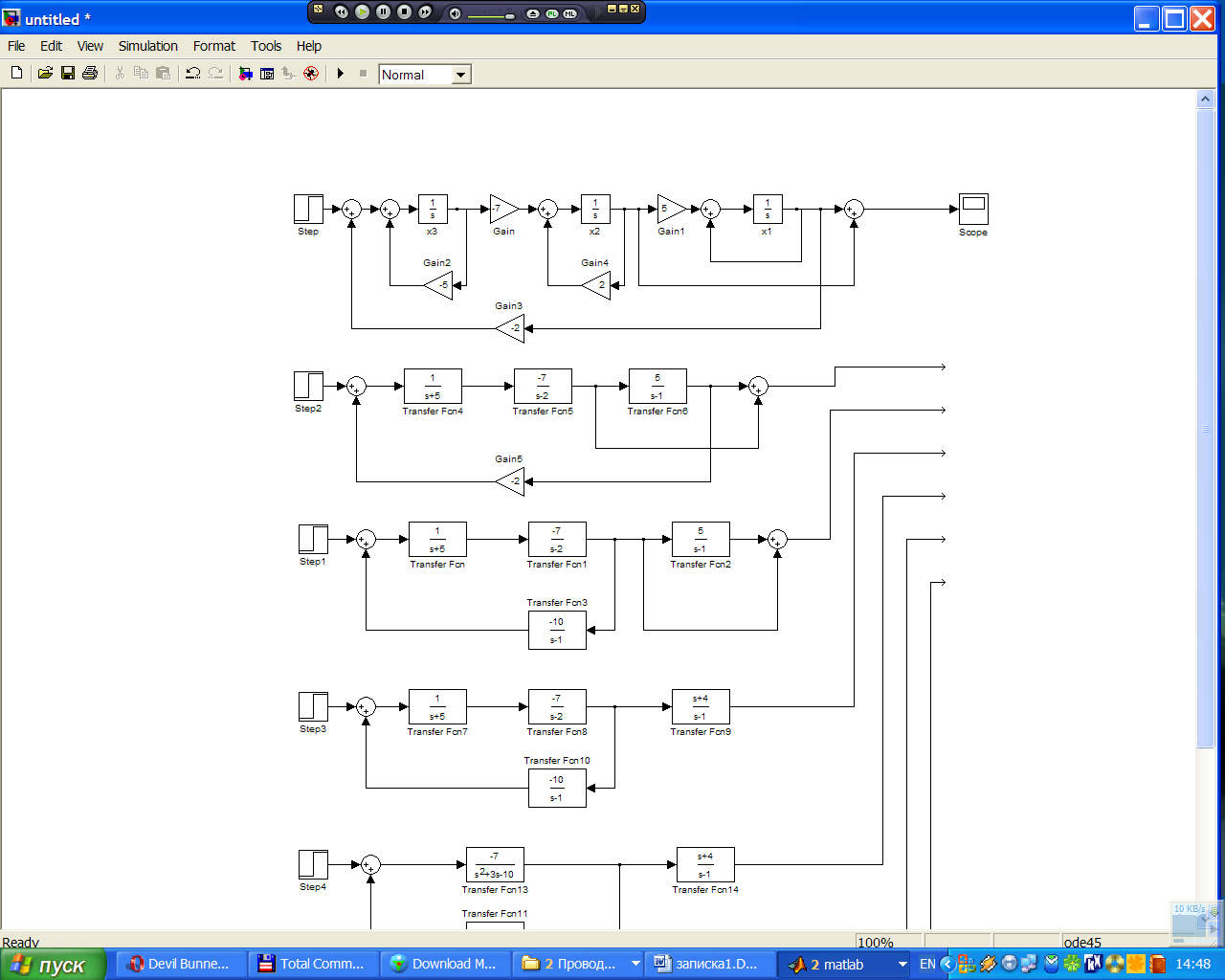
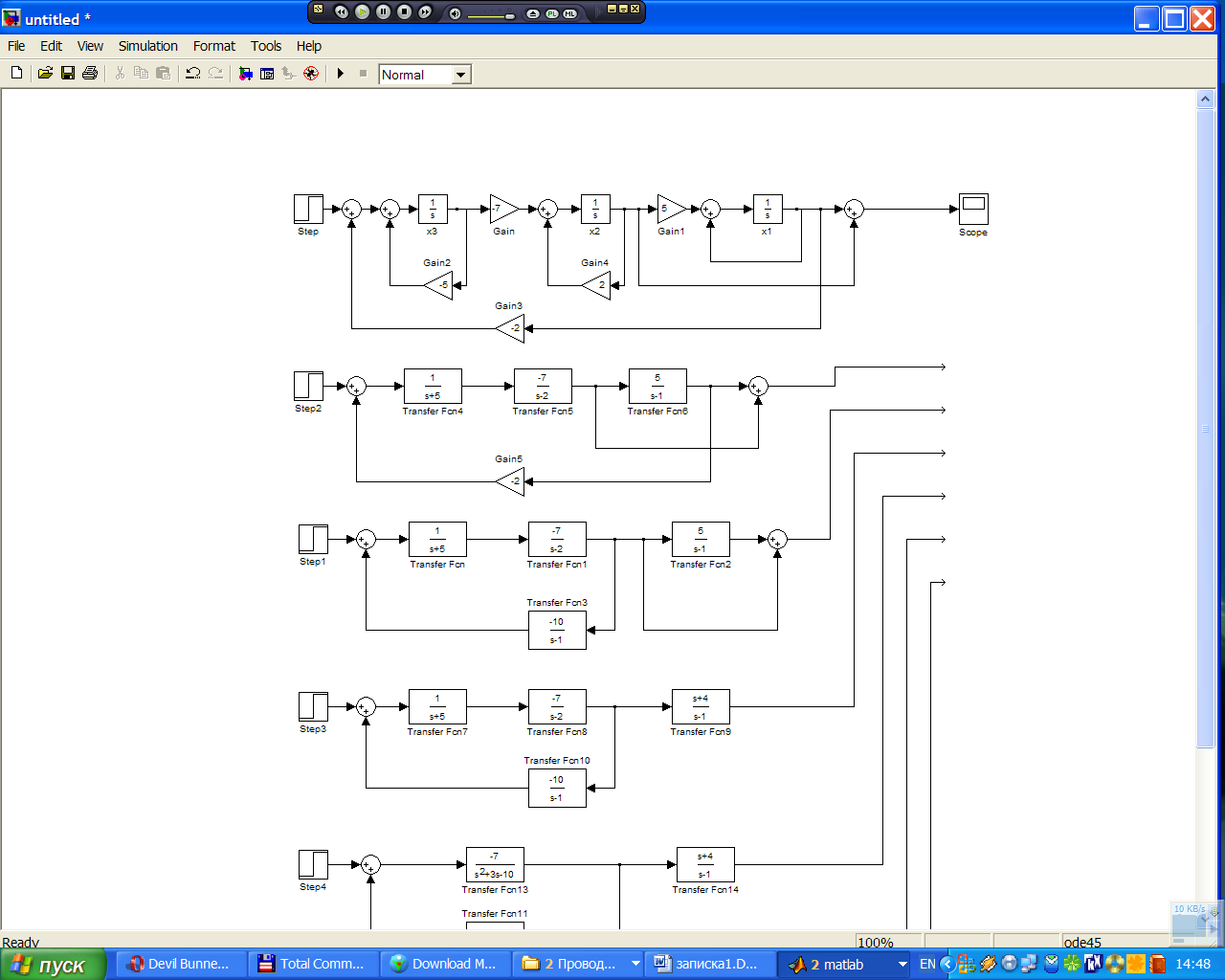
Рисунок 2.2 – Части структурной схемы, подлежащие замене

Передаточные функции, для замены фрагментов структурной схемы, будут вычисляться по формуле 2.1.

(2.1)

где W_n(s) – передаточная функция нового блока,

W(s) – передаточная функция блока, охваченного обратной связью,

W_ос – передаточная функция обратной связи.

Следовательно, передаточная функция для третьего фрагмента схемы представлена формулой 2.2.

(2.2)

Передаточная функция для второго фрагмента представлена формулой 2.3.

(2.3)

Передаточная функция для первого фрагмента представлена формулой 2.4.

(2.4)

Теперь структурная схема системы будет иметь вид, представленный на рисунке 2.3.

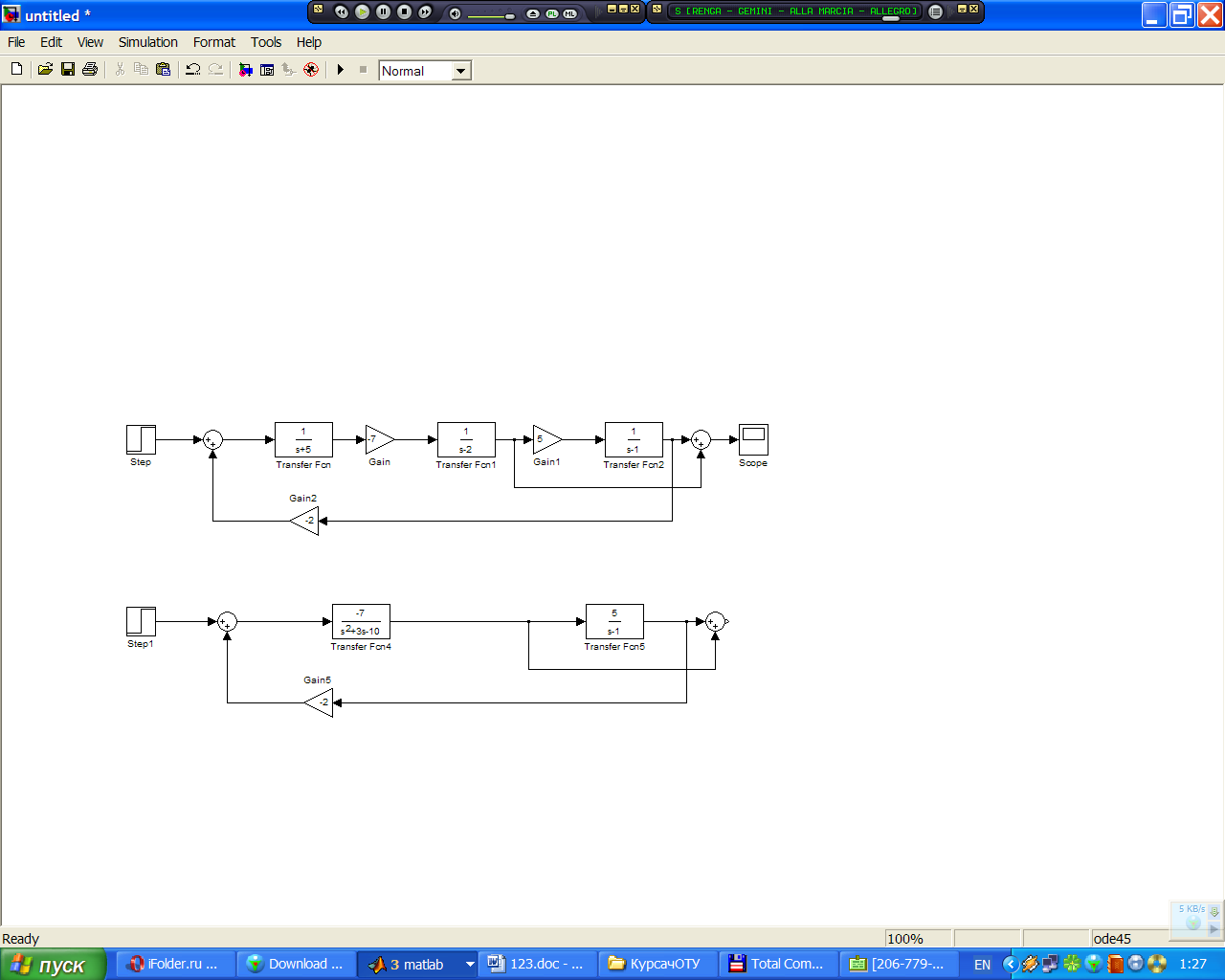
Рисунок 2.3 – Структурная схема системы после замены фрагментов

Так как некоторые звенья в полученной схеме соединены последовательно, их можно заменить одним блоком.

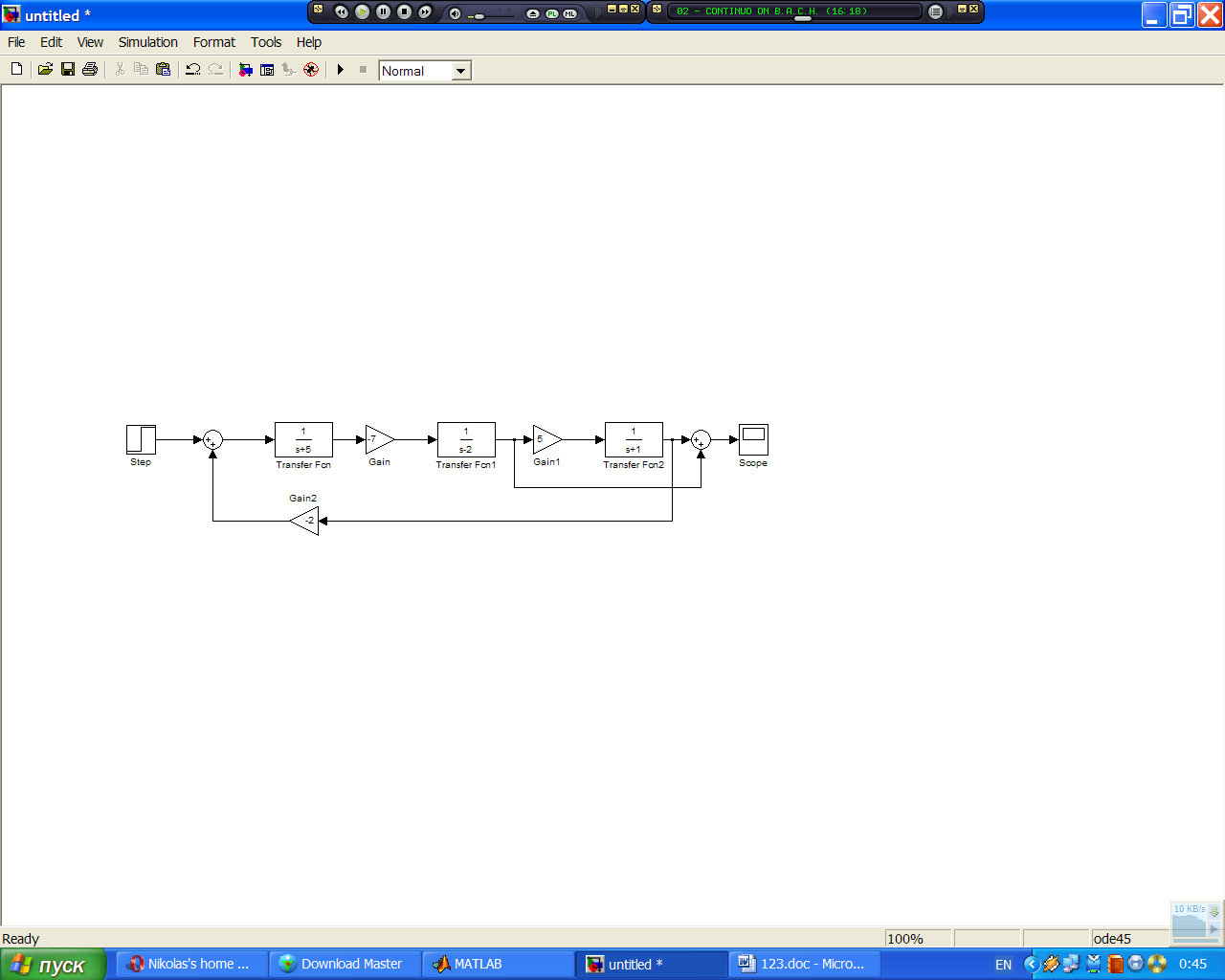
Рисунок 2.4 – Части структурной схемы, подлежащие замене

Передаточная функция этих блоков будет равна произведению передаточных функций звеньев, которые подлежат замене.

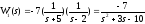
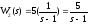
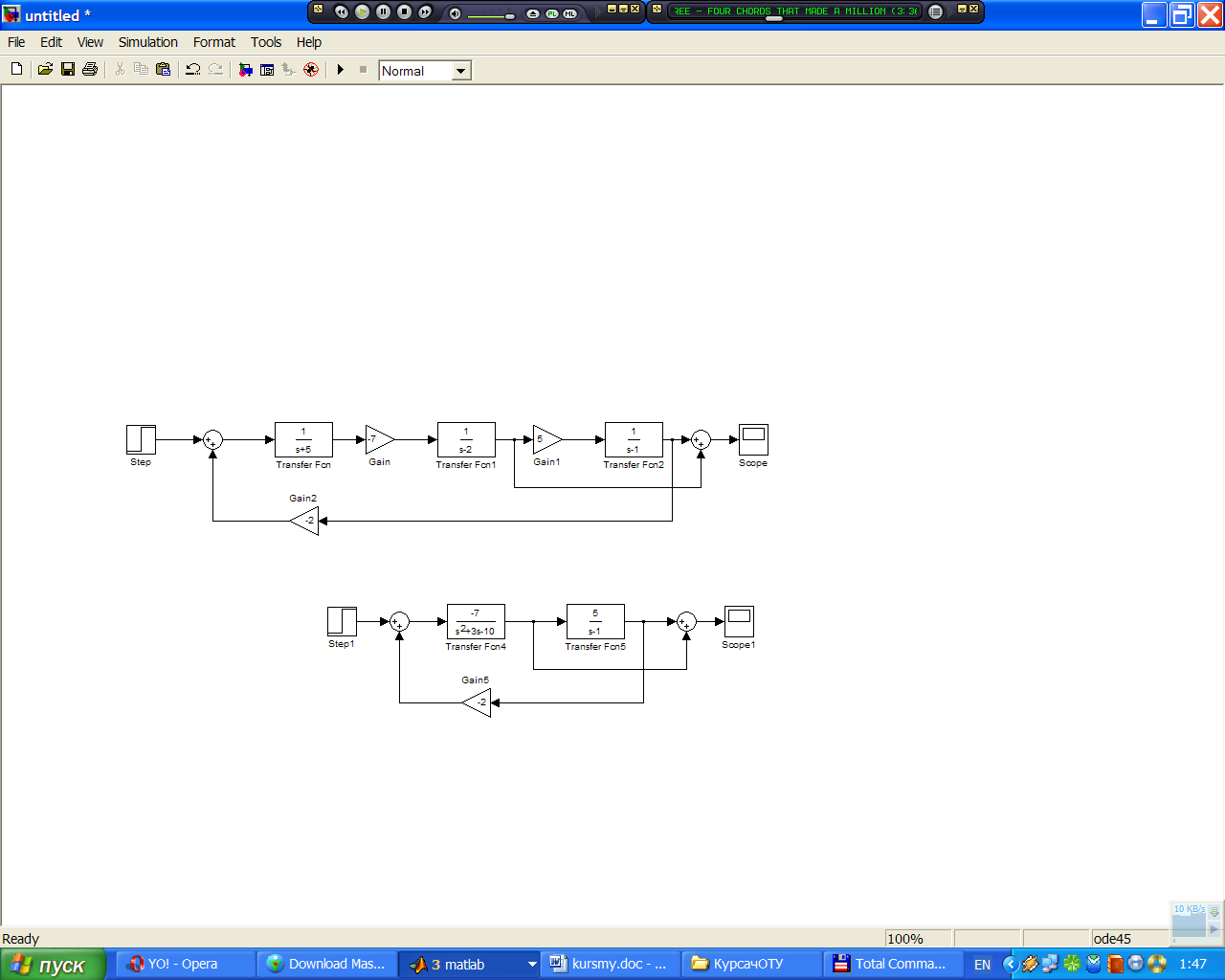
Рисунок 2.5 – Структурная схема системы после замены последовательного соединения звеньев

Перенесем первую справа точку влево через звено. Для этого в цепь обратной связи введём дополнительный блок, передаточная функция которого равна передаточной функции блока, через который происходит перенос. В нашем случае:

Рисунок 2.6 – Структурная схема системы после перестановки

точки

Заменим фрагмент, приведенный на рисунке 2.7, используя формулу 2.1.

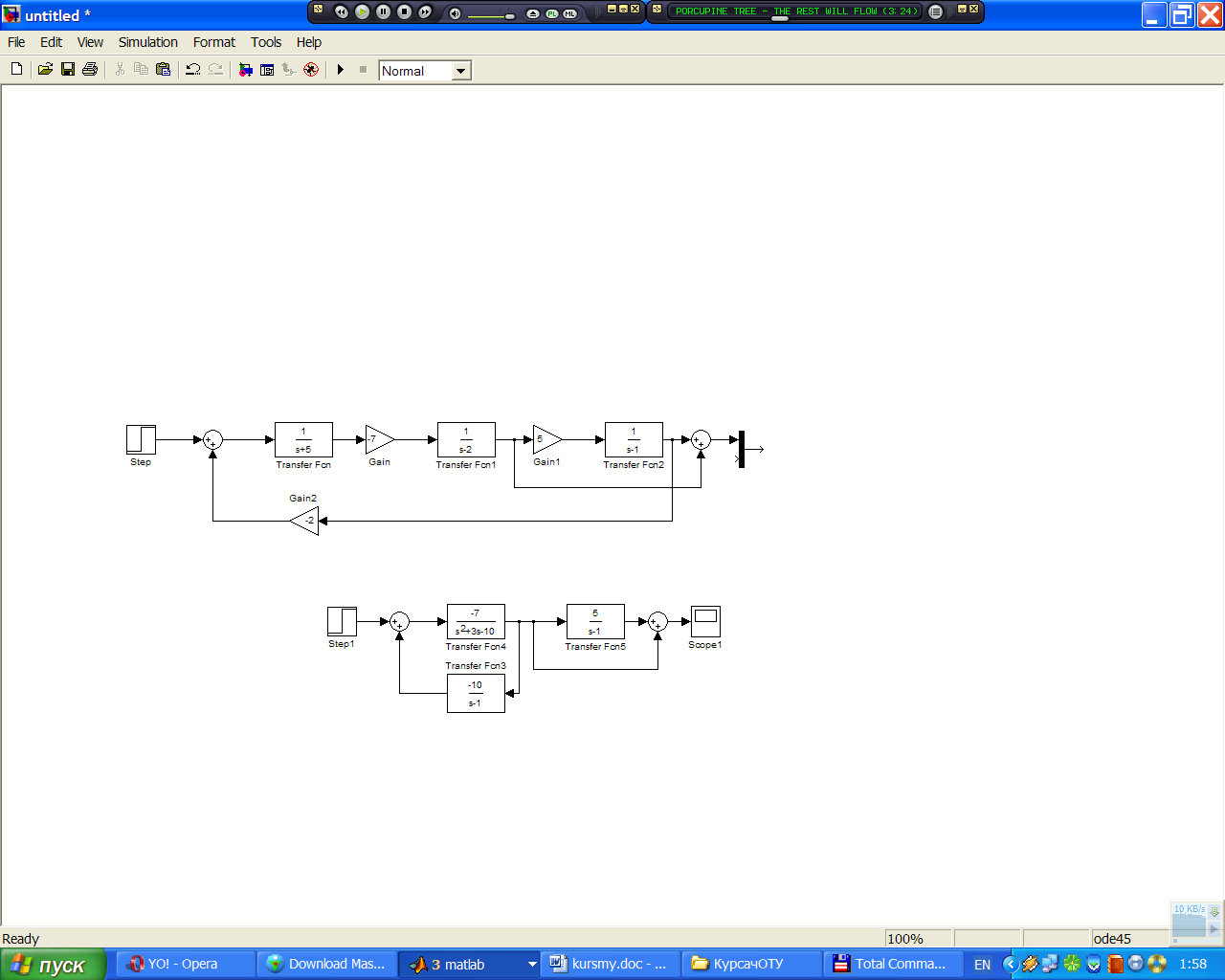
Рисунок 2.7 – Часть структурной схемы, подлежащая замене

В нашем случае получаем:

(2.6)

Рисунок 2.8 – Структурная схема системы после замены фрагментов

Сократим фрагмент системы представленный на рис. 2.9

Рисунок 2.9 – Фрагмент схемы системы, подлежащий упрощению

Получим:

(2.10)

Перемножим два оставшихся блока:

(2.11)

Полученная после данных преобразований структурная схема и будет конечной. Она представлена на рисунке 2.10.

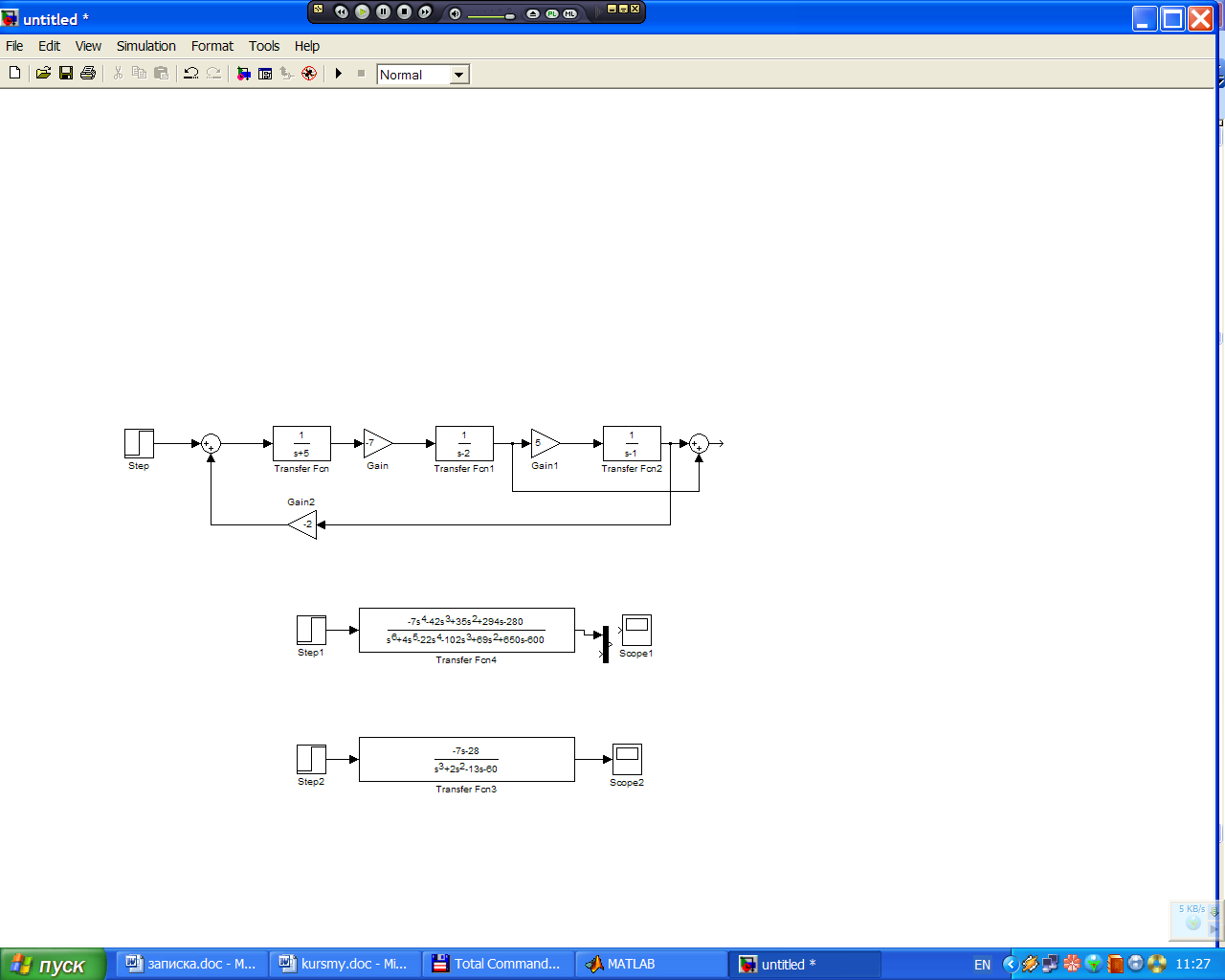
Рисунок 2.10 – Конечный вид структурной схемы системы

Протестируем структурную схему объекта на каждом шаге преобразования при помощи пакета прикладных программ SIMULINK системы MatLab. В результате в окне осциллографа получим один тот же график (рис. 2.11), который подтверждает правильность наших преобразований.

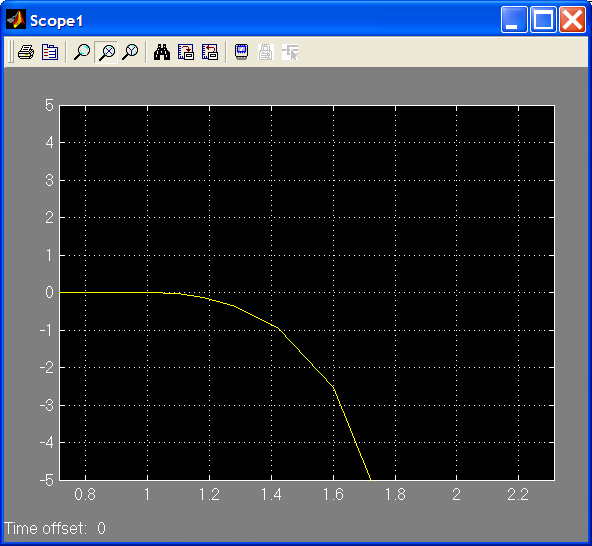
Рисунок 2.11 – График тестирования структурной схемы