3 Динамические характеристики линейной системы

Основными динамическими характеристиками любой линейной системы являются переходные и частотные характеристики.

1)Переходная характеристика (рис.3.1) представляет собой график изменения во времени выходной величины, вызванного подачей на вход системы ступенчатого единичного воздействия (функции Хевисайда), определяемого следующим образом:

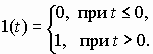
и обозначается h(t). Данная характеристика переходной функции и все рассмотренные далее характеристики находились вручную, для более подробного понятия характеристик на практике. Далее будут приводиться по паре графиков, один из которых найден вручную (прикладная среда программирования в MathLab – M-File), а второй найден автоматически с помощью рабочей среды MathLab 6.5. Переходную характеристику находим в зависимости от времени t. Функцию h(t) можно найти следующим образом:

зная что ,

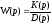
где pk – корни характеристического уравнения

Если применить данное уравнение к текущим данным, то функция Хевисайда будет выглядеть следующим образом:

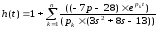
Функция данной характеристики можно построить с помощью программы, алгоритм которой выглядит следующим образом:

function ttt()

s{1}=4.2901

s{2}=-3.1451 + 2.0234i

s{3}=-3.1451 - 2.0234i

k=0

for i=0:0.01:0.6

k=k+1

for j=1:1:3

w1{j}=(-7*s{j}-28)*exp(s{j}*i)/(s{j}*(3*s{j}^2+4*s{j}-13))

end;

w(k)=28/60+w1{1}+w1{2}+w1{3}

y(k)=i

end;

plot(y,w)

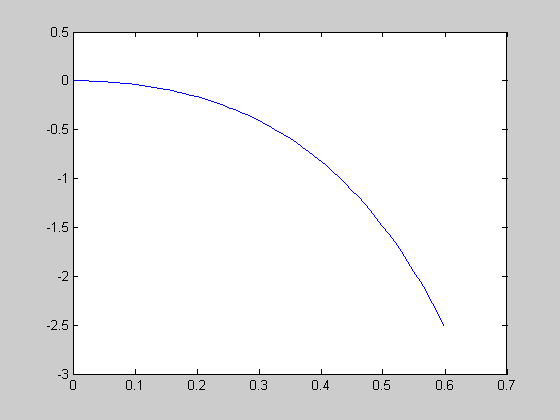
Рисунок 3.1 – Переходная функция линейной системы (вручную)

После этого для проверки правильности решения был построен график с помощью графического приложения MathLab.

>> w=tf([-7 -42 +35 +294 -280],[1 4 -22 -102 69 650 -600]);

>> step(w)

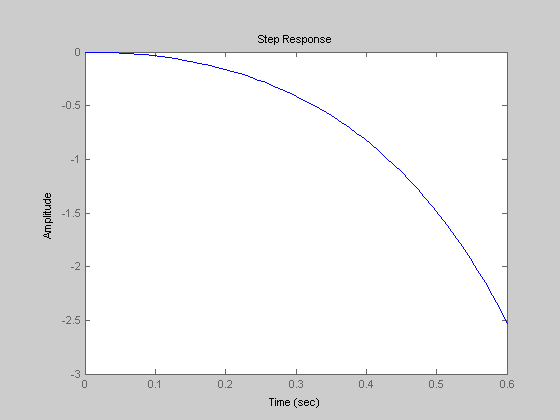
Рисунок 3.2 – Переходная функция линейной системы

Можно заметить, что графики, полученные вручную и автоматически идентичны. Это доказывает правильность нахождения функции.

2)Если на вход системы поступает единичный импульс (функция Дирака, δ -функция, импульсная функция) определяемая как:

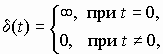
то реакция САУ называется импульсной переходной функцией системы (рис.3.2) и обозначается w(t). Функцию w(t) можно найти следующим образом:

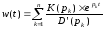
Если применить данное уравнение к текущим данным, то функция Дирака будет выглядеть следующим образом:

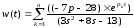
Функция данной характеристики можно построить с помощью программы, алгоритм которой выглядит следующим образом:

function imp()

s{1}=4.2901

s{2}=-3.1451 + 2.0234i

s{3}=-3.1451 - 2.0234i

k=0

for i=0:0.1:0.6

k=k+1

for j=1:1:3

w1{j}=(-7*s{j}-28)*exp(s{j}*i)/((3*s{j}^2+4*s{j}-13))

end;

w(k)=w1{1}+w1{2}+w1{3}

y(k)=i

end;

plot(y,w)

По данной функции был построен график, который выглядит следующим образом:

Рисунок 3.3 – Импульсная переходная функция линейной системы

(вручную)

>> w=tf([-7 -42 +35 +294 -280],[1 4 -22 -102 69 650 -600]);

>> impulse(w)

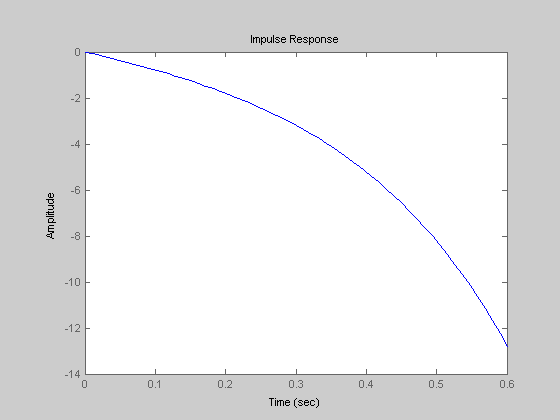
Рисунок 3.4 – Импульсная переходная функция линейной системы

Частотной характеристикой W(jω) стационарной динамической системы называется преобразование Фурье переходной функции:

,

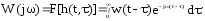где w(t - τ ) - импульсная переходная функция.

Связь между комплексной передаточной функцией и частотной характеристикой определяется соотношением:

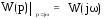
При фиксированном значении ω частотная характеристика является комплексным числом, и, следовательно, может быть представлена в виде:

,

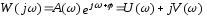где:

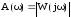
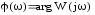- амплитудно-частотная характеристика (АЧХ), - фазово-частотная характеристика (ФЧХ), 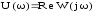- вещественная частотная характеристика (ВЧХ), 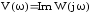- мнимая частотная характеристика (МЧХ).

Отделим действительную часть функции от мнимой:

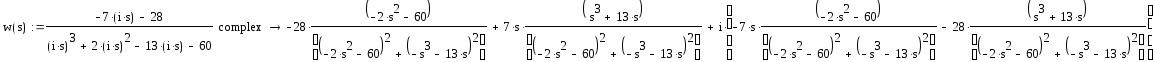
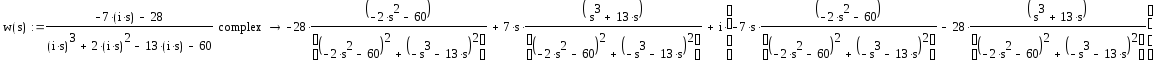
Геометрическое место точек W(jω) на комплексной плоскости при изменении ω от ω₀ до ω ₁ (обычно ω ₀ = 0, ω ₁ =  ) называется амплитудно-фазовой характеристикой (АФХ) или частотным годографом Найквиста. Функция данной характеристики можно построить с помощью программы, алгоритм которой выглядит следующим образом:

function niq()

k=0

for i=-2:0.01:2

k=k+1

w(k)=10^i

P(k)=(-28*(-2*w(k)^2-60)+7*w(k)*(w(k)^3+13*w(k)))/((-2*w(k)^2-60)^2+(-w(k)^3-13*w(k))^2)

Q(k)=(-7*w(k)*(-2*w(k)^2-60)-28*(w(k)^3+13*w(k)))/((-2*w(k)^2-60)^2+(-w(k)^3-13*w(k))^2)

Q1(k)=-Q(k)

end;

plot(P,Q,P,Q1)

где P(k) - вещественная частотная характеристика (ВЧХ),

Q(k) - мнимая частотная характеристика (МЧХ),

i – логарифмическая шкала

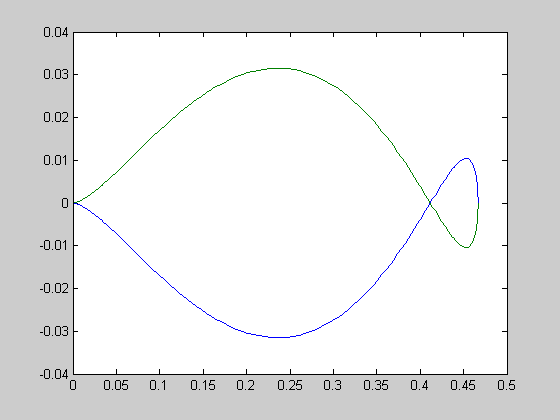
Рисунок 3.5 – Частотный годограф Найквиста линейной системы

(вручную)

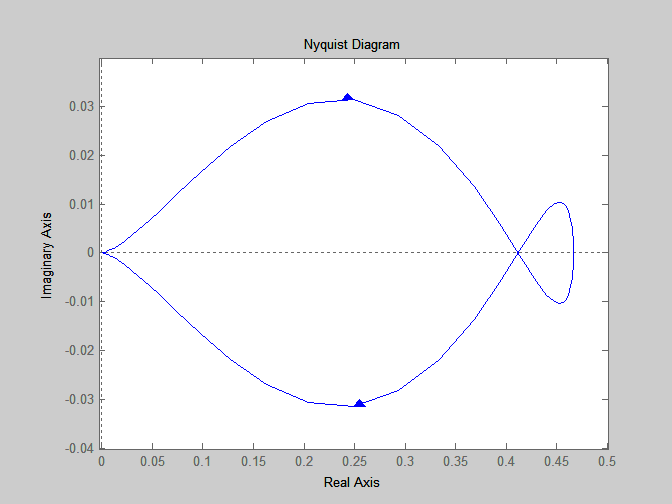
Рисунок 3.6 – Частотный годограф Найквиста линейной системы

Имеет широкое практическое значение диаграмма Боде (логарифмическая амплитудная частотная характеристика, ЛАЧХ), которая представляет собой 2 графика: первый из которых ЛАХ - L=20lgA(ω), а второй график ЛФХ – φ=atg(U(w)/V(w)),

где АЧХ

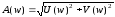
Измеряется в децибелах и строится как функция от lg (ω). Функция Боде была построена вручную по следующим алгоритмам:

function bod()

k=0

for i=-2:0.01:2

k=k+1

w(k)=10^i

P(k)=(-28*(-2*w(k)^2-60)+7*w(k)*(w(k)^3+13*w(k)))/((-2*w(k)^2-60)^2+(-w(k)^3-13*w(k))^2)

Q(k)=(-7*w(k)*(-2*w(k)^2-60)-28*(w(k)^3+13*w(k)))/((-2*w(k)^2-60)^2+(-w(k)^3-13*w(k))^2)

A(k)=(P(k)^2+Q(k)^2)^0.5

L(k)=20*log10(A(k))

end;

semilogx(w,L)

Рисунок 3.7 – Диаграмма Боде линейной системы(ЛАХ) (вручную)

function bod1()

k=0

for i=-2:0.02:2

k=k+1

w(k)=10^i

P(k)=(-28*(-2*w(k)^2-60)+7*w(k)*(w(k)^3+13*w(k)))/((-2*w(k)^2-60)^2+(-w(k)^3-13*w(k))^2)

Q(k)=(-7*w(k)*(-2*w(k)^2-60)-28*(w(k)^3+13*w(k)))/((-2*w(k)^2-60)^2+(-w(k)^3-13*w(k))^2)

fi(k)=atan(Q(k)/P(k))*180/3.14

t(k)=i

end;

semilogx(w,fi)

Рисунок 3.8 – Диаграмма Боде линейной системы(ЛФХ)

Далее для сравнения на рисунке 3.9 представлена диаграмма Боде построенная автоматически:

>> w=tf([-7 -42 +35 +294 -280],[1 4 -22 -102 69 650 -600]);

>> bode(w)

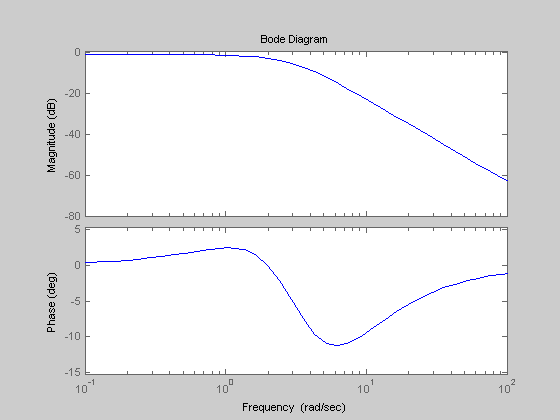
Рисунок 3.9 – Диаграмма Боде линейной системы