1.6 Определение устойчивости системы по критерию Михайлова

Необходимо, чтобы годограф Михайлова прошел последовательно все квадранты.

Характеристическое уравнение имеет вид:

Получим характеристический вектор и выделим в нем вещественную и мнимую части:

Построим годограф Михайлова:

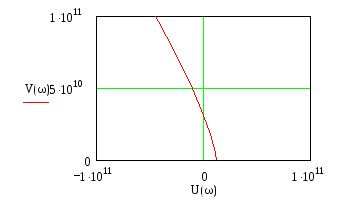
Рисунок 5 – Годограф Михайлова

Из графика видно, что система является неустойчивой, так как годограф Михайлова не проходит последовательно все квадранты, а уходит в бесконечность во втором квадранте.

1.7 Построение переходного процесса системы

Переходная функция - это реакция системы на ступенчатое входное воздействие.

Для того, чтобы построить переходный процесс используем обратное преобразование Лапласа:

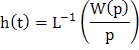
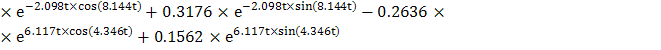
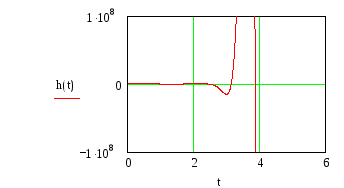
Рисунок 6 – Переходная функция системы

Анализируя график, можно судить о том, что полученная линейная система неустойчива. Прямые оценки качества системы определить невозможно.

1.8 Построение амплитудно-частотной характеристики системы

АЧХ строится для того, чтобы определить косвенные оценки качества системы.

Для того, чтобы определить АЧХ системы, необходимо в передаточной функции заменить р на , знаменатель уравнения помножить на сопряженное выражение, выделить мнимую и вещественную части по формулам определить АЧХ.

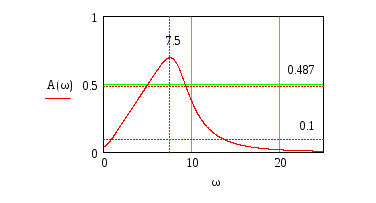
Рисунок 7 – Амплитудно-частотная характеристика системы

Определим косвенные оценки качества системы:

- амплитуда при нулевой частоте A(0)=0.145;

- максимальная амплитуда Аmax=0.69;

- резонансная частота - это частота, при которой амплитуда максимальна

- частота среза - это частота, при которой амплитуда равна 0.1

- полоса пропускания – это диапазон частот от до , который определяется при срезе величиной

, . Следовательно ;

- период колебаний

- показатель колебательности

-величина перерегулирования

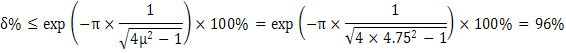
- время регулирования

1.9 Определение запаса устойчивости системы по логарифмической амплитудно- частотной характеристике и логарифмической фазо-частотной характеристике

По данной передаточной функции построим ЛАЧХ и ЛФЧХ

ЛАЧХ и ЛФЧХ изображены на рисунке 8.

По аппроксимированной ЛАЧХ определим передаточную функцию:

Запасы устойчивости по амплитуде и частоте определить невозможно, т.к. система является неустойчивой. Это видно по графикам: ЛАЧХ не пересекает нулевую амплитуду, а ЛФЧХ не пересекает

, рад/с

дБ

-40 дБ/дек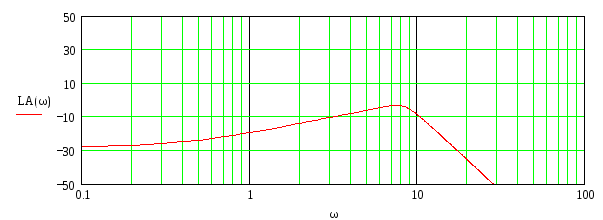

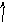
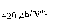
, рад/с

дБ

Рисунок 8 – Логарифмическая амплитудно-частотная характеристика и логарифмическая фазо-частотная характеристика системы

2 Исследование нелинейной части системы

2.1 Техническое задание

Рисунок 9 – Структурная схема нелинейной системы автоматического регулирования

Графическая характеристика нелинейного элемента приведена на рисунке10.

Рисунок 10 – Релейная статическая характеристика нелинейного элемента

2.2 Упрощение структурной схемы нелинейной системы автоматического регулирования

Применяя правила преобразования структурных схем, упростим схему, изображенную на рисунке9, преобразовав последовательно – параллельные соединения звеньев:

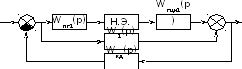
Рисунок 11 – Структурная схема нелинейной системы автоматического регулирования после преобразования последовательно-параллельных соединений звеньев

Определим передаточные функции представленные на рисунке 11:

Вынесем элементы W_пг1(p) и W_гцн1(p) за параллельную связь:

Рисунок 12 – Структурная схема нелинейной системы автоматического регулирования после преобразования

Определим передаточные функции представленные на рисунке 12:

Так как звенья и оказывают на состояние системы незначительное воздействие, то в дальнейшем будем рассматривать систему без них:

Рисунок 13 – Итоговое преобразование системы автоматического регулирования с нелинейным элементом

3. Построение фазового портрета нелинейной системы автоматического регулирования

Об устойчивости системы будем судить по фазовому портрету. Построение фазового портрета будем вести методом припасовывания. Но, сначала рассмотрим данную нам нелинейную характеристику элемента с ограничениями.

Из рисунка 10 следует следующее:

По определению передаточной функции имеем:

Подставляя в эту формулу значение передаточной функции получим:

В знаменателе данной передаточной функция выражения в пятой степени, то есть характеристическое уравнение линейной части нелинейной САР имеет пятую степень.

Степени больше второй - степени для более низких частот, оказывают небольшое влияние на систему в целом, поэтому мы можем ими пренебречь.

Следовательно можем записать, что:

Приведенную формулу можно записать в виде:

Воспользуемся пакетом MathCad для решения этого дифференциального уравнения.

Введем замену и исключим из правой части уравнения производную:

Перенесем влево:

Так как в качестве нелинейного элемента используется реле со статической характеристикой, представленной на рис.10, то подставляя значение для двух участков, получим систему:

Создадим матрицу для решения дифференциального уравнения в программе MathCad:

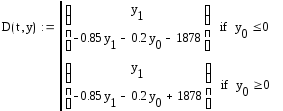
В данной матрице реализовано условие перехода от одного уравнения к другому. Зададим матрицы для трех начальных условий:

Возьмем количество точек равным 1000 и конечное время интегрирования 200, то матрица решений запишется как:

Построим фазовый портрет:

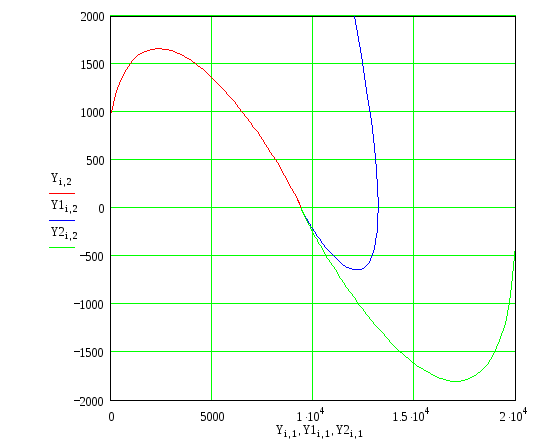
Рисунок 14 – Фазовый портрет нелинейной системы

Построим переходные процессы нелинейной системы.

, с

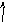
Рисунок 15 – Переходный процесс нелинейной системы

Вывод.

На рисунке 14 представлен фазовый портрет нелинейной системы. Из графика видно, что при различных начальных условиях система будет оставаться устойчивой. С течением времени процесса амплитуда колебаний будет уменьшаться, система придет к устойчивому равновесию – точке (9390.7;0) на рисунке 14, то есть произойдет процесс переключения. Устойчивость системы подтверждает график переходного процесса рисунок 15.

ЗАКЛЮЧЕНИЕ

В ходе данной курсовой работы, была рассмотрена система передачи тепловой энергии от теплоносителя первого контура, к питательной воде второго контура. Были получены функциональная и структурная схемы системы. Исследована линейная, и нелинейная части системы.

В ходе исследования линейной системы, была получена передаточная функция, по которой был построен переходный процесс, который свидетельствовал об не устойчивости линейной системы. Также система оказалась не устойчивой по критерию Гурвица и годографу Михайловаа. Определены прямые и косвенные оценки качества системы

Нелинейная система была получена путем введения нелинейного элемента с заданной статической характеристикой. В ходе исследования полученной системы был построен фазовый портрет – сходящаяся в точке кривая. Следовательно введение нелинейного элемента в систему оказало положительное влияние на устойчивость системы.

СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ

1. Автоматизация и современные технологии / Под ред. Анисимова. М: 2005 №12.

2. Айзерман М.А. Теория автоматического регулирования. 2- е издание. – М.: Наука,1966. – 452 с.

3. Бесекерский В.А. Теория систем автоматического регулирования/ В.А. Бесекерский, Е.П. Попов. – М.: Профессия, 2003. – 380 с.

4. Климовицкий М.Д. Автоматический контроль и регулирование: Справочник. – Л.: Металлургия, 1987. – 345 с.

5. Кошарский Б.Д., Бек В.А. Автоматические приборы и регуляторы. – Ь.: Машиностроение, 1964. – 704 с.

6. Лапшинков Г.И., Полоцкий Л.М. Автоматизация производственных процессов в химической промышленности. Технический средства и лабораторные работы. – М.: Химия, 1988. – 288 с.

7. Летов А.М. Устойчивость нелинейных регулируемых систем. – М.: Физматгиз, 1962. – 315 с.

8. Обновленский П.Л., Гуревич А.Л. Основы автоматизации химических производств. – М.: Химия, 1975. – 328 с.

9. Поспелов Г.С. Импульсные системы автоматического регулирования. – М.: Машгиз, 1950. – 256 с.

10. Промышленные приборы и средства автоматизации: Справочник/ В.Я. Баранов. Л.: Машиностроение, 1987. – 847 с.

11. Пугачев В.С.Основы автоматического регулирования. – М.: Наука, 1974. –720 с.

12. Топчеев Ю.И. Атлас для проектирования систем автоматического управления. – М.: Машиностроение, 1982. – 312 с.

21

УИТС.421434.226 ПЗ

Дата

Подп.

№ докум.

Лист

Изм.

Лист