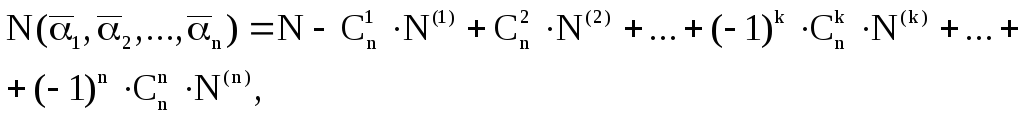- •Правило произведения Теоретико – множественная формулировка правила произведения
- •Комбинаторная формулировка правила произведения
- •Сложный выбор объектов
- •Соединения без повторений
- •Перестановки
- •Размещения из n элементов по m
- •Решение:
- •Сочетания
- •Основные понятия комбинаторики: соединения с повторениями
- •Размещения с повторениями
- •Сочетания с повторениями
- •Формулы пересчета для основных видов комбинаторных соединений
- •Принцип включения- исключения
- •Частные случаи формулы включений и исключений
- •Задача о беспорядках
- •Задача o встречах
- •Перестановки без фиксированных пар
- •Распределение объектов по ячейкам
- •Распределение одинаковых объектов
- •Вместимость ячеек задана
- •Распределение различных объектов по ячейкам с учётом их порядка в различных ячейках Вместимость ячеек неограниченна, ячейки могут быть пустыми
- •Вместимость ячеек неограниченна, ячейки не могут быть пустыми
- •Варианты к индивидуальному заданию по комбинаторике
- •Вариант №1.
- •Вариант №2.
- •Вариант №3.
- •Вариант №4.
- •Вариант №5.
- •Вариант №6.
- •Вариант №7.
- •Вариант №8.
- •Вариант №9.
- •Вариант №10.
- •Вариант №11.
- •Вариант №12.
- •Вариант №13.
- •Вариант №14.
- •Вариант №15.
- •Вариант №16.
- •Вариант №17.
- •Вариант №18.
- •Вариант №19.
- •Вариант №20.
- •Вариант №21.
- •Вариант №22.
- •Вариант №23.
- •Вариант №24.
- •Вариант №25.
- •Вариант №26.
- •Вариант №27.
- •Вариант №28.
- •Вариант №29.
- •Вариант №30.
- •Контрольные вопросы
Частные случаи формулы включений и исключений
1.Если все
свойства
![]() попарно несовместны, т.е.
попарно несовместны, т.е.
![]() ,
то формула имеет вид:
,
то формула имеет вид:
![]()
2.Если каждое число
![]()
зависит не от характера свойств, от их
количества, то формула приобретает вид:
зависит не от характера свойств, от их
количества, то формула приобретает вид:
где
![]() - число объектов, обладающих k свойствами.
- число объектов, обладающих k свойствами.
3.Для упрощения применения формулы включений и исключений предлагается следующий формальный прием:
обозначим![]() ,
тогда
,
тогда
![]() .
.
Введем правила раскрытия скобок:
![]() .
.
Например:
при
![]() имеем:
имеем:
Такая формальная запись позволит найти число объектов, обладающих одними и не обладающих другими свойствами, например:
![]() .
.
Задача о беспорядках
Пусть множество
![]() .
Рассмотрим перестановки элементов
множества
.
Рассмотрим перестановки элементов
множества
![]() .
.
Элемент
![]() перестановки называется неподвижным,
если
перестановки называется неподвижным,
если
![]() ,
т.е. элемент стоит на своем месте.
,
т.е. элемент стоит на своем месте.
Например:
при
![]()
5 2 4 3 1 – элемент “2” – неподвижный;
1 2 3 4 5 – все элементы неподвижны.
Беспорядком называется перестановка,
не имеющая неподвижных элементов, т.е.
![]()
Постановка задачи:
Определить
![]() -
количество беспорядков в n-элементном
множестве, или количество перестановок
чисел
-
количество беспорядков в n-элементном
множестве, или количество перестановок
чисел
![]() таких, что
таких, что
![]() ?
?
![]() называют субфакториалом.
называют субфакториалом.
Решение:
Общее число перестановок –
![]() .
.
Обозначим через
![]() такое свойство перестановки, когда i-й
элемент стоит на своем месте, т.е. аi
= i.
такое свойство перестановки, когда i-й
элемент стоит на своем месте, т.е. аi
= i.
![]() -
число перестановок, обладающее свойством
-
число перестановок, обладающее свойством
![]() ,
т.е.
,
т.е.
![]() .
.
![]() - в этих перестановках только один
элемент находится на своем месте,
остальные – в беспорядке.
- в этих перестановках только один
элемент находится на своем месте,
остальные – в беспорядке.
![]() ,
т.к. число перестановок не зависит от
того, какой именно элемент находится
на своем месте.
,
т.к. число перестановок не зависит от
того, какой именно элемент находится
на своем месте.
Обозначим через
![]() - количество перестановок, в которых
только два элемента находятся на своих
местах,
- количество перестановок, в которых
только два элемента находятся на своих
местах,
![]() ,
,![]() …
,
…
,
![]() –
количество перестановок, в которых
только
–
количество перестановок, в которых
только
![]() элементов находятся на своих местах
элементов находятся на своих местах
![]()
![]() .
.
По формуле включений-исключений имеем:
![]() (1)
(1)
Распишем формулу:
Задача o встречах
Постановка задачи:
Определить количество таких перестановок
![]() чисел
чисел
![]() ,
что точно
,
что точно
![]() элементов
из
элементов
из
![]() находятся на своих на местах (т.е.
находятся на своих на местах (т.е.
![]() ),
а остальные
),
а остальные
![]()
![]() находятся в беспорядке.
находятся в беспорядке.
Иначе: нас
интересуют перестановки, в которых
точно
![]() элементов неподвижны.
элементов неподвижны.
Решение:
Из общего числа элементов некоторым
образом выбирается
![]() ,
которые остаются на своих местах,
остальные
,
которые остаются на своих местах,
остальные
![]() элементов находятся в беспорядке.
Количество способов, которыми можно
переставить
элементов находятся в беспорядке.
Количество способов, которыми можно
переставить
![]() элементов при таких условиях, равно
элементов при таких условиях, равно
![]() .
.
Перестановки без фиксированных пар
Постановка задачи: Обозначим через
![]() - число таких перестановок
- число таких перестановок
![]() чисел
чисел
![]() ,
что ни одна из этих перестановок не
содержит ни одной из упорядоченных пар
,
что ни одна из этих перестановок не
содержит ни одной из упорядоченных пар
![]() .
.
Решение:
Для вычисления
![]() используем принцип включения и исключения.
Будем говорить, что перестановка обладает
свойством
используем принцип включения и исключения.
Будем говорить, что перестановка обладает
свойством
![]() ,
если она содержит i–тую упорядоченную
пару (i, i+1). Число всех перестановок
,
если она содержит i–тую упорядоченную
пару (i, i+1). Число всех перестановок
![]() .
.
Перестановки, обладающие свойством
![]() ,
получаются как перестановки элементов
,
получаются как перестановки элементов
![]() и пары
и пары
![]() ,
рассматриваемой как один элемент.
Следовательно, независимо от
,
рассматриваемой как один элемент.
Следовательно, независимо от
![]() .
.
Перестановки, обладающие двумя свойствами,
т.е. имеющие две упорядоченные пары,
например
![]() и
и
![]() ,
получаются из пар
,
получаются из пар
![]() ,
каждая из которых рассматривается как
отдельный элемент и
,
каждая из которых рассматривается как
отдельный элемент и
![]() оставшихся элементов, т.е. из (n-2)
элементов.
оставшихся элементов, т.е. из (n-2)
элементов.
Если к=i+1 , то перестановки составляем из (i, i+1, i+2) и (n-3) остальных элементов, т.е. тоже из (n-2) элементов.
![]() независимо от
независимо от
![]() и
и
![]() .
Число перестановок, не обладающих ни
одним из свойствами
.
Число перестановок, не обладающих ни
одним из свойствами
![]() ,
зависит только от
,
зависит только от
![]() и
и
![]() .
.
Всего пар может быть - (n-1), следовательно:
![]()