Сочетания с повторениями

Пусть А = {a₁, a₂,…, a_n}, где a₁, a₂,…, a_n - “представители” 1-го, 2-го, …, n-го типа элементов. Объектов каждого типа имеется в неограниченном количестве, элементы одного типа неразличимы между собой.

Сочетания с повторениями отличаются составом элементов, входящих в выбираемое множество. Порядок элементов не имеет значения. Имеет значение, сколько элементов каждого типа вошло в сочетание. Рассмотрим определенное сочетание.

Пусть в него входят: r₁ объектов 1-го типа,

r₂ объектов 2-го типа,

. . . . . . . . . .

r_n объектов n-го типа;

.

Н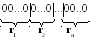 екоторые r_i могут быть равны 0. Сочетанию можно поставить в соответствие следующую схему:

Вертикальные черточки отделяют элементы одного типа от элементов другого. Если элементов какого-либо типа нет, две черты будут рядом. Количество черточек равно (n-1). Каждому сочетанию с повторениями соответсвует схема и наоборот, каждая подобная схема соответствует некоторому сочетанию с повторениями.

Количество сочетаний с повторениями из n по m равно числу таких схем.

Всего в схеме (n – 1) + m объектов, (n – 1) – черточек и m – нулей. Число схем равно числу различных перестановок из (n + m – 1) – элементов, среди которых (n – 1) – одинаковых “ | ” и m – одинаковых “0”.

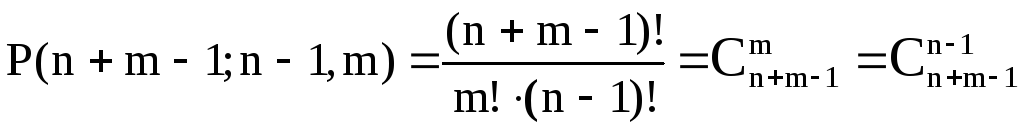
Число различных сочетаний с повторениями из n по m равно:

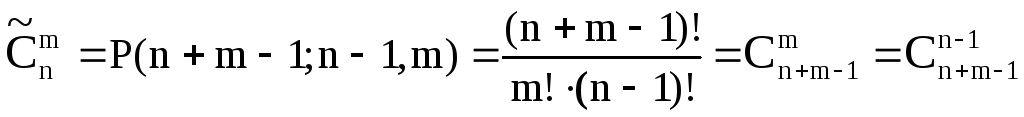
Например:

1) В кондитерской продают 4 вида пирожных. Сколькими с пособами один человек может купить 8 пирожных?

2 ) В кондитерской продают 4 вида пирожных. Сколькими способами 8 различных человек могут купить по 1 пирожному?

Формулы пересчета для основных видов комбинаторных соединений

С оединения	Без повторений элементов	С повторениями элементов
Сочетания
Размещения
Перестановки

Принцип включения- исключения

Пусть имеется n объектов и множество свойств . Каждый объект может обладать или не обладать одним или несколькими свойствами .

Введем ряд обозначений.

– количество объектов, обладающих свойством .

– количество объектов, не обладающих свойством .

– количество объектов, обладающих двумя свойствами .

– количество объектов, обладающих тремя свойствами .

– количество объектов, обладающих всеми свойствами .

– количество объектов, не обладающих ни одним из n свойств .

Формула включений и исключений определяет количество объектов, не обладающих ни одним из свойств, заданных множеством .

При произвольном справедлива следующая формула включений и исключений:

Например:

На фирме работает 67 сотрудников. Из них 47 владеют английским языком, 35 -немецким, 20-французским; одновременно английским и немецким владеют – 23 человека, английским и французским-12, немецким и французским-11, тремя языками владеют 5сотрудников. Сколько человек не владеют ни одним языком?

Решение:

Определим следующие свойства:

– “владеть английским языком”;

– “владеть немецким;

– “владеть французским”.

По формуле включений и исключений имеем:

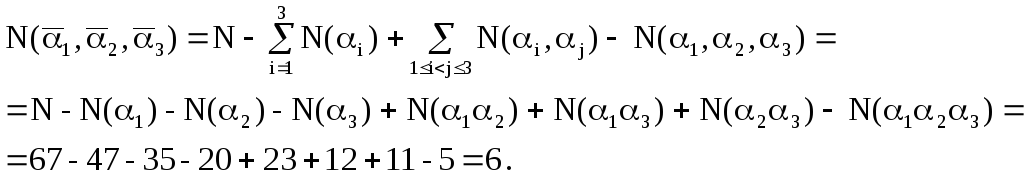
Шесть человек не владеют ни одним из перечисленных языков.