II.3. Составление структурной схемы сар.

Теперь, зная математическое описание отдельных элементов САР, получим структурную схему системы.

Рис.3. Структурная схема.

III. Передаточная функция и дифференциальное уравнение разомкнутой исходной системы.

Передаточная функция разомкнутой системы определяется как произведение передаточных функций всех звеньев системы

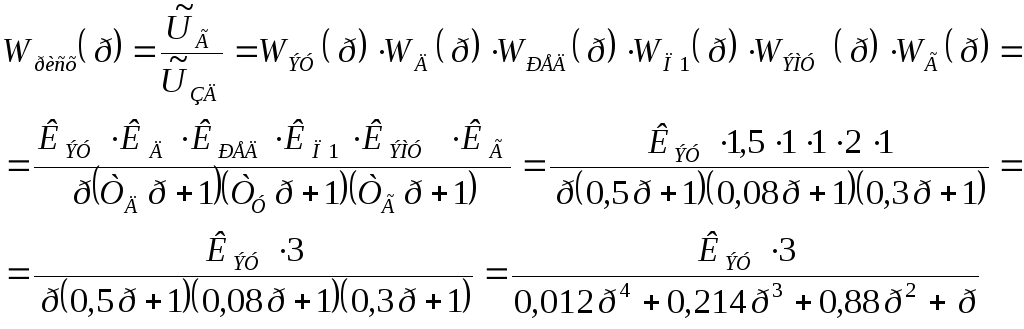
Отсюда получим дифференциальное уравнение разомкнутой исходной системы

.

IV. Определение общего коэффициента усиления (добротности) системы.

Добротность системы К, обеспечивающая заданную точность Δ=2,75% =0,0275, определяется из выражения

В правой части дифференциального уравнения разомкнутой исходной системы сомножитель и есть добротность системы, поэтому

.

Отсюда

.

V. Передаточная функция и дифференциальное уравнение замкнутой исходной системы.

С учетом полученного значения передаточная функция исходной разомкнутой системы примет вид

Дифференциальное уравнение исходной разомкнутой системы при будет выглядеть так

.

Передаточная функция исходной замкнутой системы в случае отрицательной единичной обратной связи определится из выражения

.

В нашем случае

Дифференциальное уравнение исходной замкнутой системы будет

VI. Определение устойчивости исходной замкнутой системы. Нахождение граничного коэффициента усиления.

Для определения устойчивости исходной замкнутой САР воспользуемся алгебраическим критерием Гурвица. Характеристическое уравнение замкнутой системы получим из передаточной функции , приравняв нулю ее знаменатель

Коэффициенты этого характеристического уравнения в стандартных для критерия Гурвица обозначениях таковы

а₀ = 0,012; а₁ = 0,214; а₂ = 0,88; а₃ = 1; а₄ = К = 35,4

Согласно критерию Гурвица для устойчивости системы, заданной некоторым характеристическим уравнением, необходимо и достаточно, чтобы при положительности всех коэффициентов характеристического уравнения были бы положительны и все главные диагональные миноры. В нашем случае все коэффициенты а_i (i = 0,1,2) положительны, проверим знаки миноров.

Так как минор , то система в замкнутом состоянии неустойчива.

Определим граничный коэффициент К_гр , при котором система находится на границе устойчивости. Для этого приравняем нулю минор и из полученного равенства найдемК_гр.

.

Отсюда

.

Следовательно

.

Итак, исходная система неустойчива, поэтому необходим синтез корректирующего устройства.

VII. Построение желаемой лачх. Определение устойчивости, расчет и построение переходной характеристики скорректированной системы.

VII.1 Построение исходной лачх.

Для синтеза САР воспользуемся методом В.В.Солодовникова, базирующимся на построении логарифмических амплитудно-частотных характеристик (ЛАЧХ) исходной и желаемой систем и получении ЛАЧХ корректирующего устройствав соответствии с выражением

.

Построим ЛАЧХ исходной системы

.

Этой передаточной функции соответствует амплитудно-фазовая и амплитудно-частотная характеристики

Отсюда выражение для точной ЛАЧХ запишется в виде

Сопрягающие частоты исходной ЛАЧХ находятся следующим образом

Так как передаточная функция исходной разомкнутой системы относится к III типу, то для первого участка асимптотической ЛАЧХ, т.е. для , уравнение асимптоты ЛАЧХ будет.

Это уравнение прямой линии с наклоном -20 дб/дек, проходящей при ω = 1с через точку . Дальнейший ход асимптотической ЛАЧХ при увеличении частоты характеризуется тем, что на сопрягающих частотахω_с1, ω_с2, ω_с3 происходит изменение наклона характеристики каждый раз на -20 дб/дек (рис.4).

Рис.4. ЛАЧХ исходной САР, желаемой САР и корректирующего устройства.