Лекция № 22

СИНТЕЗ ДИСКРЕТНЫХ СИСТЕМ МЕТОДОМ

ЖЕЛАЕМЫХ ЧАСТОТНЫХ ХАРАКТЕРИСТИК.

План лекции:

1. Требования к динамике системы и их учет при решении задачи синтеза.

2. Построение желаемых логарифмических псевдочастотных характеристик.

3. Непрерывная коррекция импульсных систем.

22.1. Требования к характеристикам системы и их учет при решении задачи синтеза.

Задача синтеза состоит в построении системы, обладающей желаемыми характеристиками.

Одним из наиболее распространенных методов синтеза является метод желаемых логарифмических амплитудно-частотных характеристик (ЖЛАЧХ), позволяющий сформировать систему с требуемыми статическими и динамическими характеристиками. При его использовании задается неизменяемая часть системы и указываются возможности введения тех или иных корректирующих устройств. Требования, предъявляемые к системе, формулируются как требования к ее логарифмическим амплитудным псевдочастотным характеристикам (ЛАПЧХ).

Метод ЖЛАЧХ позволяет учитывать следующие основные требования:

а) требования к точности системы в установившемся режиме;

б) требования к запасам устойчивости и качеству процессов управления (колебательность, перерегулирование и так далее);

в) требования к быстродействию системы.

Для импульсных систем, помимо перечисленных требований могут формулироваться требования непосредственно к цифровому алгоритму управления, например, алгоритм коррекции должен быть устойчивым, может быть задан максимальный порядок алгоритма коррекции и так далее.

В соответствии с этими требованиями строятся желаемые ЛАПЧХ (ЖЛАПЧХ). Задача синтеза состоит в определении корректирующего устройства, при котором система в целом имеет характеристики, близкие к желаемым.

Рассмотрим, каким образом при построении ЖЛАПЧХ учитываются требования, предъявляемые к системе.

Требования к точности часто формулируются как требования к величине ошибки в установившемся режиме при отработке типового воздействия. Типовым воздействием обычно является гармонический сигнал с амплитудой Авх и частотой , то есть:

.

Ошибка , устанавливающаяся в системе по окончании переходного процесса, определяется выражением:

, (22.1)

где - передаточная функция замкнутой системы по ошибке.

Из приведенной выше формулы (22.1) следует, что :

.

Если ошибка не должна превышать известную величину , то для этого достаточно потребовать, чтобы, то есть

.(22.2).

Как известно из ранее рассмотренного материала, связь между ПФ разомкнутой системы W(z) и ПФ для одноконтурной импульсной системы задается выражением:

.

Так как на частоте обычно справедливо приближенное равенство:

,

то условие (22.2) можно записать в виде:

Учитывая, что в рабочем диапазоне частот псевдочастота приближено равна действительной круговой частоте, в последнем выражении можно перейти к псевдочастоте:

, (22.3)

где .

Неравенство (22.3) представляет собой ограничение, накладываемое на низкочастотную часть ЛАПЧХ. ЛАПЧХ разомкнутой ИС должна проходить выше точки с координатами:

.

Требования к точности ИС могут формулироваться различным образом. Например, для статической системы может быть задана допустимая ошибка отработки единичного ступенчатого воздействия. Тогда коэффициент усиления системы должен удовлетворять условию:

.

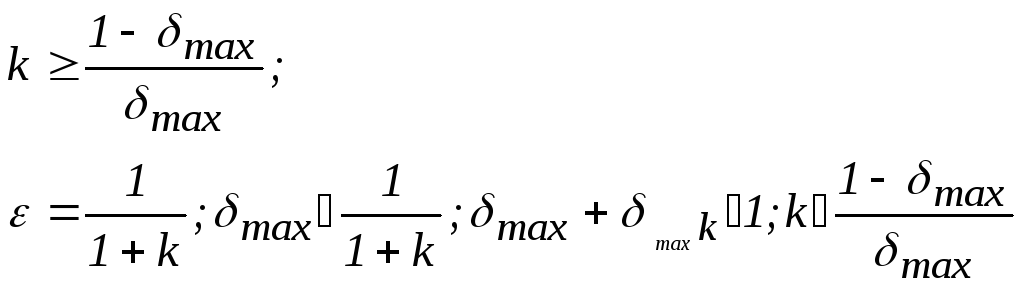Устойчивость замкнутой системы может контролироваться с помощью запасов устойчивости. Понятие запасов устойчивости по амплитуде и фазе даны при рассмотрении ЛАПЧХ. Отметим только, что обычно принимают запасы устойчивости по амплитуде и фазе не менее 10 Дб и 30⁰ соответственно.

Показатели качества переходного процесса, как и для непрерывных систем обычно определяются при воспроизведении системой ступенчатого входного сигнала. Это такие показатели, как время переходного процесса, перерегулирование и так далее.

Требования, предъявляемые к качеству переходного процесса, трудно сформулировать количественно в терминах частотных характеристик. Практически они обычно проверяются уже после синтеза, с помощью численного расчета переходных процессов в синтезируемой системе. Здесь возможны лишь некоторые частные рекомендации. Например, если в низкочастотной области, вплоть до частоты среза ЛАФЧХ ИС и приведенной НЧ совпадают, то для предварительной оценки времени регулирования и перерегулирования могут быть применены методы теории непрерывных систем. С помощью известных номограмм в зависимости от времени регулирования и перерегулирования может быть выбрана частота среза для ЖЛАХ приведенной НЧ, совпадающая с.