Умножение оригиналов
Теорема 7. Если решетчатая функция
и
является оригиналом, то произведение
этих функций
также является оригиналом и выполняется
равенство:
Здесь
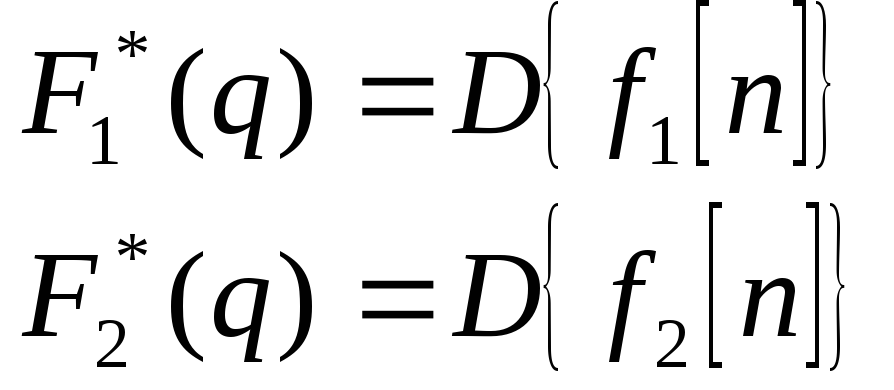
И должно выполняться условие:
Где
и
- показатели роста функций
и
.
Доказательство:
Так как
и
- оригиналы, то для них справедливы:
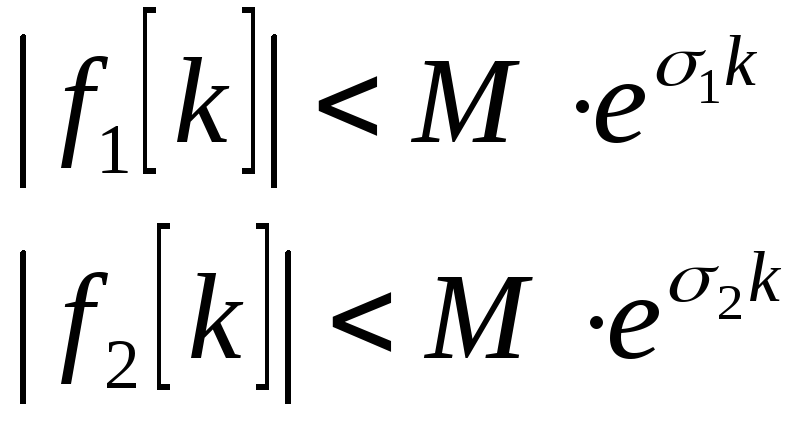
И отсюда следует оценка модуля произведений этих двух функций:
Здесь
и
.
Таким образом
является оригиналом с показателем роста
.
Теперь применяя D-преобразование
функции
,
получим:
Используя формулу прямого D-преобразования и равенство:
мы получим:
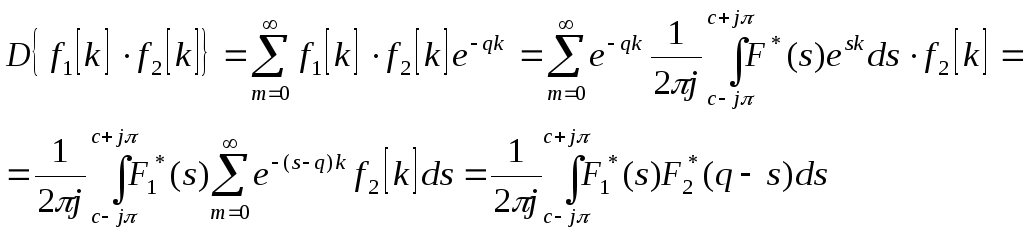
Изменение порядка суммирования и
интегрирования, которые мы применили,
законно, если сходится равномерно ряд
.
Для этого должно выполняться условие
или
.
Если
всегда выполняется, то получим
.
Величину
можно
выбрать сколь угодно близкой к
.
Теорема доказана.