Умножение изображений
Определим свертку
решетчатых функций
и
по формуле:
(1)
С учетом этого определения сформулируем следующую теорему:
Теорема 6. Если
и
- оригиналы, то свертка этих функций
также является оригиналом, причем
изображение свертки равно произведению
изображений
и
.
То есть справедливо равенство:
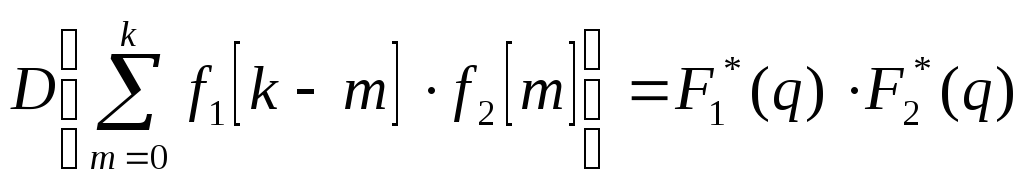(2)
При этом есть дискретное преобразование Лапласа от соответствующих функций:
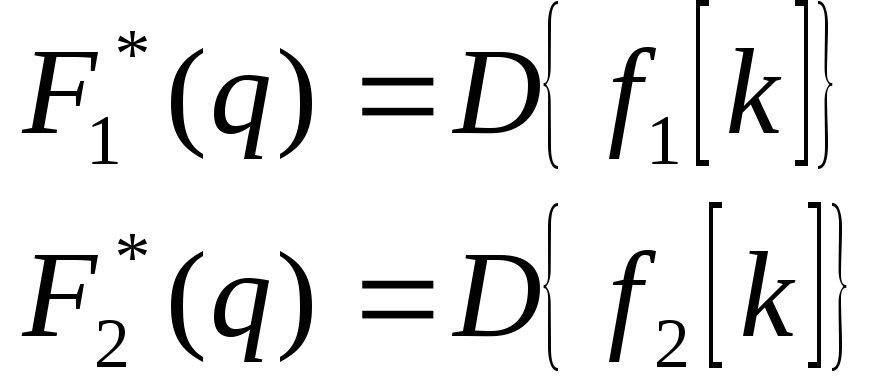
Доказательство:
Выполним умножение изображений:
В результате почленного переумножения двух рядов получим ряд, состоящий из всех попарных произведений:
Теперь сгруппируем члены полученного
ряда при равных степенях
:
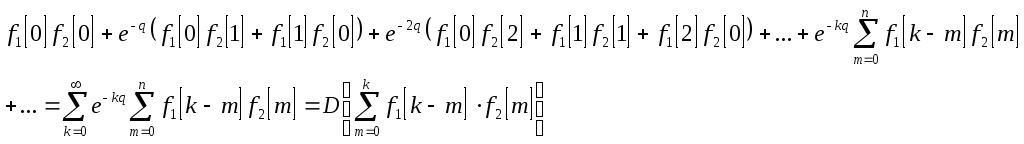Это
совпадает с уравнением (2). Покажем, что
свертка двух функций, которые являются
оригиналами, также являются оригиналом.
Так как функции
и
- оригиналы, то должны выполняться два
условия:
Получим следующую оценку для свертки
функций
и
:
Пусть
-
это наибольший из двух чисел от
и
.
Тогда последнее неравенство примет
вид:
Теперь отметим, что при любом
и
для сколь угодно малого
справедливо:
А это означает, что выполняется неравенство:
А это значит, что справедлива следующая оценка:
Таким образом, мы доказали, что свертка двух оригиналов является также оригиналом.