Теорема 1

Пусть , когда, такое допустимое управление, что соответствующая ему траектория, исходящая прииз точки, проходит в момент временичерез некоторую прямую П. Для оптимальности управленияи траекториинеобходимо существование такой ненулевой непрерывной вектор-функции, которая соответствует функциями, что:

1. При любом 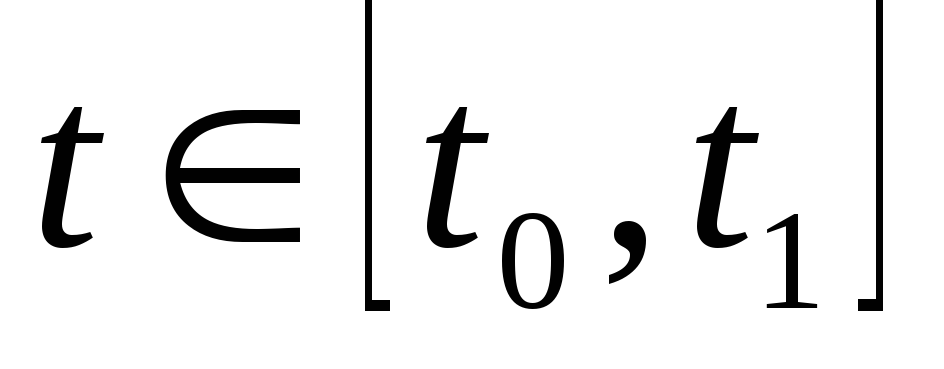функция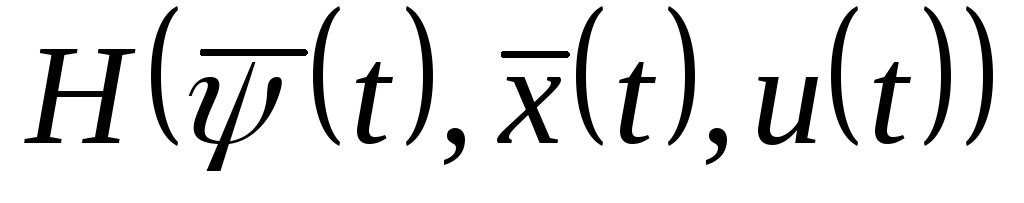достигает помаксимума, то есть справедливо равенство:

(11)

2. В конечный момент времени 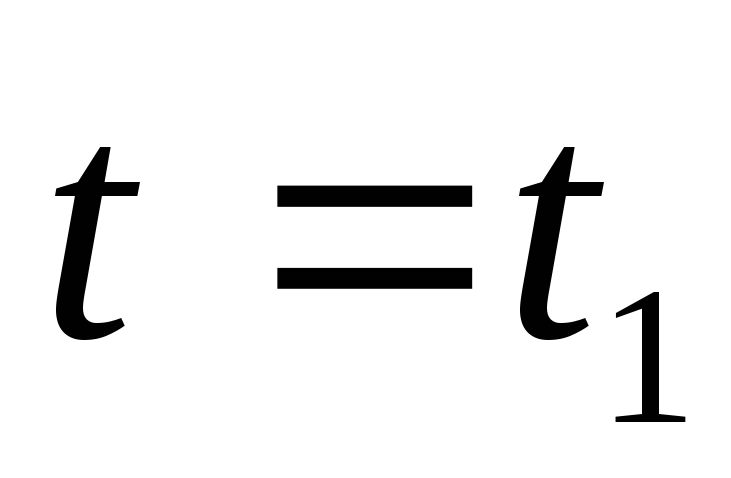имеют место соотношения:

(12)

Можно показать, то если вектор-функции удовлетворят уравнениям (9) и (10), то функциииявляются постоянными, так что проверку условий (12) можно проводить в любой момент времени их интервала.

Если начальная точка и конечная точкане фиксирована в пространствеX, а принадлежит начальному многообразиюразмерностии конечного многообразиюразмерности, то к условиям теоремы необходимо добавить условие трансверсальности в начальных и конечных точках.

Сказано, что n-мерная вектор-функцияудовлетворяет условию трансверсальности в начальной или конечной точке траектории, если векторилиортогональны касательной плоскости, проведенной к многообразиюв точкеили кв точке. Это иллюстрирует следующий рисунок:

Таким образом, если концы траектории не фиксированы, то вектор-функции , помимо условий (1) и (2), должны также удовлетворять условиям трансверсальности. Условие трансверсальности позволяет определитьсоотношений между координатамии.

Добавим к ним соотношений.

Это все позволяет получить достаточную систему соотношений для решения задач оптимального управления.

Доказательство

Приведем доказательство теоремы для задач со свободным правым концом и фиксированным временем .

Пусть - оптимальное управление,- соответствующая ему траектория.

Рассмотрим малый интервал времени , гдеи. Передадим управлениюприращение на промежутке, не изменяя значение управляющей функциивне этого интервала. Здесь не требуется, чтобы приращение, где, было малой величиной. Если управление ограничено неравенствами, то приращение удовлетворяет условию.

Такие вариации носят название игольчатыми вариациями.

Найдем отклонение траектории системы, которое вызвано изменением управляющей функции:

В силу непрерывности функции разностьтакже имеет порядок малости, поэтому запишем:

(13)

Из выражения (13) следует, что в момент времени вариация имеет порядок малости. Здесь выражение (14) – это вариация координат системы:

(14)

Согласно теореме о непрерывной зависимости от начальных условий, когда , вариации координат также будут иметь порядок малости. Теперь для траектории имеем соответствующую систему уравнений:

Теперь стандартный прием. Мы разложим правые части системы в ряд Тейлора:

(15)

Учитываем члены первого порядка малости.

Введем квадратичную матрицу размера частных производных:

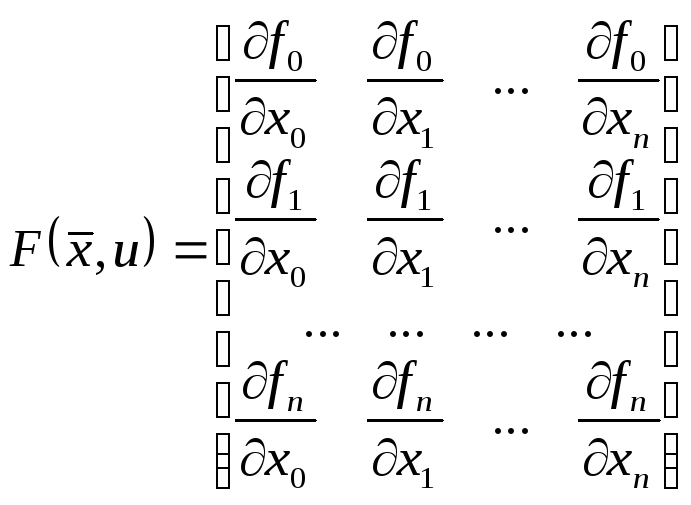
Теперь уравнение (15) запишем в векторной форме записи:

(16)

Введем в рассмотрение (n+1)-ый вектор, который удовлетворяет уравнению:

(17)

Это уравнение в координатной форме имеет вид:

Рассмотрим скалярное произведение . В силу того, что справедливо равенство:

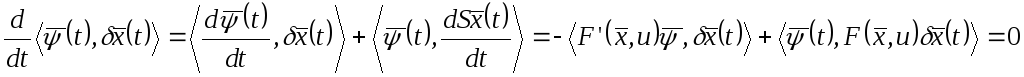
это скалярное произведение постоянно, когда .

Примем во внимание, что есть равенство . А по условию теорему управлениедоставляет заданному функционалуминимум. Тогда, для управления, отличного от оптимального, будет справедливо неравенство:

Теперь зададимся граничными условиями на векторной функции :

(18)

Тогда будет выполняться неравенство:

Учитывая, что:

получаем:

Подставляя в это неравенство выражение:

будем иметь:

Откуда получаем, с учетом :

В качестве момента времени можно выбрать любой момент из промежутка, поэтому окончательно можно записать:

где функция определена равенством (8), а- это оптимальное управление. Необходимость теоремы 1 доказана.

Граничным условиям (18) соответствует ненулевое решение системы (17). Отметим, что граничные условия (18) вытекают из условия (2) теоремы и условия трансверсальности для свободного правого конца траектории.

Покажем, что принцип максимума позволяет из всех траекторий, которые начинаются в точке и проходящих через точку, выделить лишь отдельные изолированные траектории, удовлетворяющие необходимым условиям. Лишь эти оптимальные изолированные траектории и могут оказаться оптимальными, так как принцип максимума дает лишь необходимое условие оптимальности.

Всего в формулировке принципа максимума имеется 2n+2rнезависимых функций,,и столько же соотношений. То есть имеется полная система для определения этих переменных.

Действительно, уравнение (11) в условиях теоремы дает rсоотношений между неизвестными функциями, еслиявляется внутренней точкой множестваU, то для выполнения условия максимума необходимо обращение в нульrчастных производных:

Если точка лежит на (r-1)-мерной грани областиU, то есть одна из управляющих функцийпринимает предельное значение, то должно выполняться условие принадлежности точкиэтой грани, что дает одно соотношение, и для выполнения условия максимума функционалаHдолжны обращаться в нуль ее частные производные, то есть производные функциипо всем параметрам этой грани (по всем остальным управлениям).

Помимо соотношений (11) мы имеем систему из 2n+2 уравнений (9) и (10). Таким образом из всего имеется 2n+2+rсоотношений (9), (10), (11) для определения,,неизвестных.

Общее решение уравнений (9) и (10) содержит 2n+2 производных постоянных, но одна из них несуществующей, так какявляется линейной и однородной функцией переменных.

С учетом изложенного, решение системы (9), (10), (11) зависит от 2nпараметров. Их нужно подобрать так, чтобы притраекторияпроходила через точку, а при- через точку, то есть через прямую П. Числотакже является параметром. Всего имеем 2n+1 параметров, которые подлежат определению.

Условие прохождения траектории через точку и прямую П дает 2n+1 условий, поэтому можно ожидать, что имеются отдельные изолированные траектории соединяющие точкус прямой П и удовлетворяющие требованиям теоремы принципа максимума. Если в частности условиям теоремы удовлетворяет единственная траектория, а из физических соображений ясно что оптимальная траектория существует, то найденная траектория будет оптимальной.

24