Принцип максимума л.С.Понтрягина в теории оптимальных систем

Принцип максимума определяет необходимые условия оптимальности управления в нелинейных управляющих системах. Он распространен и на случаи, когда на координаты состояния системы накладываются ограничения. Рассмотрим основную теорему принципа максимума и дадим более удобную формулировку оптимального управления.

Пусть оптимальное управление описывается системой нелинейных дифференциальных уравнений:

(1)

или в векторной форме:

Здесь:

--мерный вектор состояния объекта

--мерный вектор управляющих воздействий

- функция правой части уравнения (1)

Полагаем, что вектор управления принимает значения из некоторой замкнутой области Ur-мерного пространства управлений. Положим, что функциинепрерывны по всем аргументам и имеют непрерывные производны по переменным состояния. Назовем допустимыми управлениями те управления, которые являются кусочно-непрерывными функциями времени и принимают значения из множестваU.

Основная задача оптимального управления формулируется следующим образом: среди всех допустимых управления, приводящих изображающую точку в фазовом пространстве Xиз начального положенияв конечное, если эти управления существуют. И нужно найти такие управления, для которых функционал:

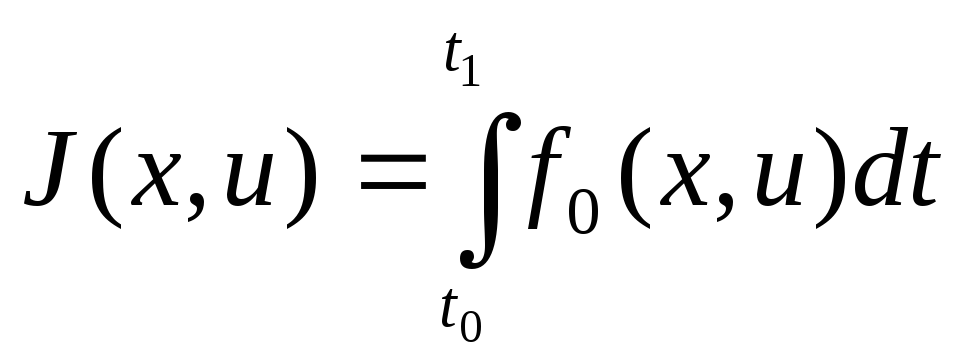(2)

достигает минимума.

Введем новую переменную , которая определяется следующим дифференциальным уравнениям:

(3)

Здесь - подынтегральная функция функционала (2).

Присоединив уравнение (3) к системе уравнений (1), получим:

(4)

Запишем (4) в векторной форме. Для этого введем в рассмотрение (n+1)-ый вектор координат состояния:, тогда в векторной форме записи это уравнение запишется следующим образом:

(5)

Здесь:

вектор правых частей системы (5).

Заметим, что вектор-функция не зависит от координатывектора. Обозначим черезточку с координатамив (n+1)-ом фазовом пространстве. Пусть- некоторое допустимое управления, для которого соответствующая фазовая траектория (1) проходит причерез точку. А при выполнении равенствачерез точку.

Из уравнения (2) следует, что координата определяется равенством:

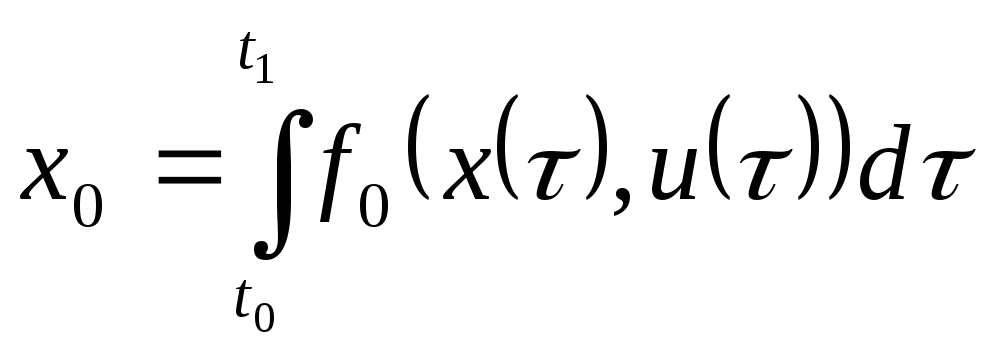
Если , то будем иметь:

Таким образом, в пространстве фазовая траектория системы (5), соответствующая тому же управлению, проходит причерез точку, а причерез точку. Это иллюстрирует следующий рисунок:

Обозначим через П прямую в пространстве , проходящую через точкуи параллельную оси. Тогда основную задачу оптимально управления можно сформулировать следующим образом:

В (n+1)-мерном пространствезаданы начальная точкаи прямая П, параллельная осии проходящую через точку. Среди всех допустимых управлений, обладающих тем свойством, что решение системы (5) с начальными условиямипроходит через точку прямой П, необходимо выбрать такое управления, для которого координата точкиимело бы минимальное значение.

Сформулированная задача представляет собой задачу Майера на условный экстремум. Однако в силу ограничений, накладываемых на допустимое управление методами классического вариационного исчисления, эта задача не решается.

Формулировка теоремы, дающей необходимое условие экстремума:

Введем в рассмотрение вспомогательные переменные , которые удовлетворяю следующей системе уравнений:

(6)

Система (6) называется сопряженной по отношению к системе уравнений (5). Если выбрать некоторое допустимое управление на отрезкеи найти соответствующее ему решениес заданными начальными условиями, то при подстановки в систему уравнений (6) управленияи решения, получим линейную однородную систему уравнений:

(7)

Система (7) удовлетворяет условиям существования и единственности решения системы дифференциальных уравнений. Системы уравнений (5) и (6) можно объединить одной формой записи, для этого надо ввести в рассмотрение функцию H:

(8)

Здесь:

Тогда системы (5) и (6) запишутся следующим образом:

(9)

(10)

Отметим, что вектор функций инепрерывны всюду, кроме точек разрыва допустимого управления. Эти вектор-функции имеют непрерывные производные. При фиксированных значенияхифункцияHстановится функцией только управления.