Решение линейной двухточечной краевой задачи методом прогонки

Идея метода прогонки содержится в самом соотношении:

Попытаемся перенести (прогнать) граничные условия к начальному моменту времени . В результате чего получим начальное значении, и затем, так как нам будет известно начальное состояние системыи значение, то можно выполнить интегрирование системы уравнений:

(1)

(2)

на интервале времени . То есть, решаем задачу Коши.

При интегрировании этой системы дифференциальных уравнений по формуле:

можно получить управление , которое доставляет минимум функционалу:

А теперь рассмотрим метод прогонки.

Полагаем, что векторы исвязаны соотношением:

(3)

Здесь - квадратичная симметричная матрица размера, которое подлежит определению.

Продифференцируем уравнение (3) по времени:

(4)

Подставим уравнения (3) и (4) в (2) и получим:

(5)

Теперь (1) подставим в (5) и вновь учтем (3) и получим:

Или:

(6)

Здесь учтено свойство симметрии матриц. То есть если - симметричная матрица, то справедливо следующее соотношение:

Так как вектор , то из уравнения (6) следует:

(7)

Это матричное дифференциальное уравнение Риккати.

Чтобы проинтегрировать выражение (7), вычислим значение при. Для этого воспользуемся равенствами:

Приравняем правые части этих равенств:

Откуда следует:

(8)

Уравнение (7) можно проинтегрировать (прогнать) от конечного значения к начальному значению. Это так называемое интегрирование в обратном времени.

После этого с помощью уравнения:

вычислим начальное значение времени .

Теперь решение системы дифференциальных уравнений (1) и (2):

где начальные значения изаданы, может быть получено путем интегрирования в прямом времени. При выполнении интегрирования системы ДУ (1) и (2) с помощью формулы:

(9)

можно вычислить уравнение системы в каждый момент времени. Отметим, что это уравнение по принципу обратной связи. При этом коэффициенты обратной связи:

являются переменными, то есть зависят от времени.

Линейная стационарная система с бесконечным временем управления

Задача формулируется следующим образом:

Имеется линейный объект управления:

(1)

Рассмотрим случай, когда . При этом критерий качества системы может быть представлен следующим образом:

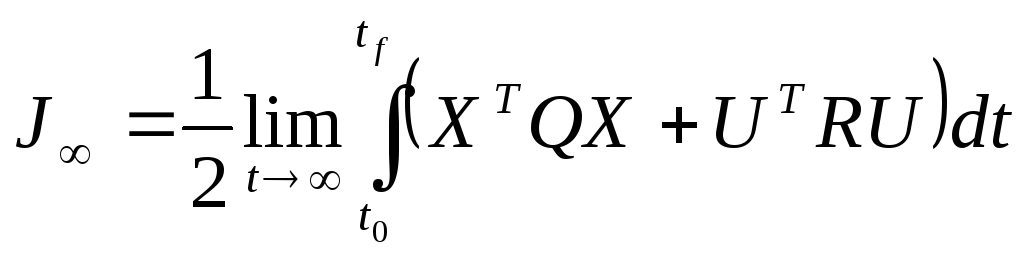(2)

Здесь и- положительно определенные матрицы.

Тогда уравнение Риккати запишется следующим образом:

(3)

Здесь, в отличие от функционала:

, то граничное условие для матрицытакже будут нулевыми:

Решение уравнения Риккати, удовлетворявшее граничным условиям, обозначим . Приэто решение имеет предел:

Здесь - постоянная симметричная положительно определенная матрица, которая является решением матричного уравнения Риккати:

(4)

В этом случае оптимальное управление принимает следующий вид:

(5)

Теперь уравнение динамики системы запишется следующим образом:

(6)

Из уравнение (5) следует, что и в этом случае оптимальное управление формируется по принципу обратной связи, и оказывается, что замкнутая система обладает свойством асимптотической устойчивости.

Задача оптимизации при ограничениях на управляющее воздействие

До сих пор мы рассматривали задачи, в которых рассматривается синтез регулятора, когда на управляющее воздействие не накладывается никаких ограничений. Это значит, что вектор управления принадлежит открытой области. Но во многих задачах управления управляющее воздействиеограничено. И наиболее часто это ограничение задается неравенствами:

(1)

А это значит, что вектор управления принадлежитr-мерному кубу.

Рассмотрим общую задачу оптимизации, которая формулируется следующим образом:

Динамика системы описывается системой ДУ:

(2)

Заданы граничные условия в начале движения системы и в конце:

(3)

Требуется определить управление , которое переводит из заданного начального состояния системы (2)в конечное, и удовлетворяет ограничениям (1), и чтобы для этого управления, и соответствующей ему траектории, функционал:

(4)

достигает минимума.

Здесь:

-n-мерный вектор состояния системы;

-r-мерный вектор управляющей функции.

Чтобы применить метод вариационного исчисления для решения этой задачи, введем в рассмотрение вспомогательные управляющие функции и вспомогательное соотношение:

(5)

Вспомогательные зависимости (5) выберем таким образом, чтобы совокупность этих равенств позволила перейти от замкнутой области изменения переменных или управляющих функций к открытой области для переменных,.

Такой переход может быть осуществлен различными способами, которые зависят от вида функции .

Например:

(6)

Если функция задана следующим образом, то для этой цели можно использовать функции вида:

(7)

Здесь:

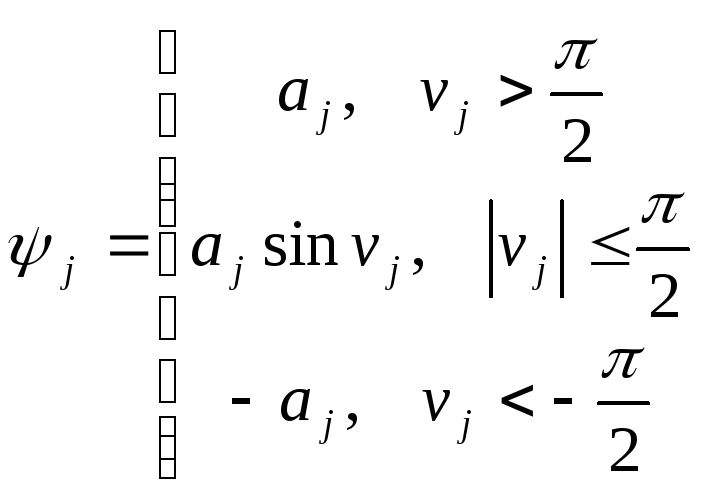
Теперь задачу оптимального управления можно сформулировать следующим образом:

Требуется определить функции ,, которые удовлетворяют условиям (5), чтобы эти управления и соответствующая траекториясистемы (2) доставляли минимум функционалу (4). Траекториядолжна удовлетворять граничным условиям (3).

Эта задача представляет собой задачу Лагранжа на условный экстремум. В соответствии с методикой решения Лагранжа введем вспомогательный функционал:

(8)

Составим уравнение Эйлера-Лагранжа:

(9.1)

(9.2)

(9.3)

В этих уравнениях через обозначена функция:

К этим уравнениям надо добавить уравнение объекта (2) и соотношение (5), которые представляют собой уравнение Эйлера-Лагранжа по переменным ,,,,для функционала (8).

В этом случае имеется переменных,,,,, для определения которых можно использоватьуравнений (9.2) и условия (5).

Для определения rпроизвольных постоянных в общем решении уравнения Эйлера-Лагранжа нужно воспользоваться граничными условиями (3). Отметим, что управления, когда, в общем случае могут представлять собой кусочно-непрерывные функции времени.

Тогда в точках разрыва непрерывности управления траекториясистемы (2) имеет излом. В этой точке должны выполняться условия Вейерштрасса - Эрмана, которые для данного случая имеют вид:

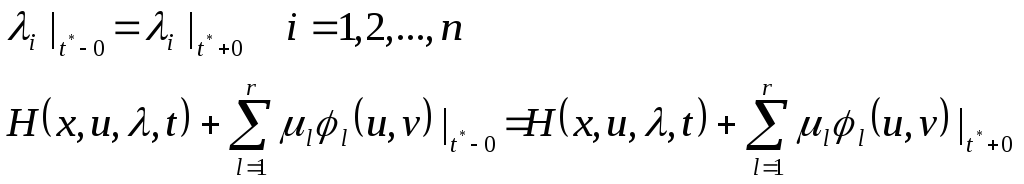(10)

Рассмотрим частный случай, когда условия (5) выбраны в виде (6), а функционал (4) принят квадратичным. Тогда, для задачи оптимизации линейной системы, которая описывается уравнениями вида:

и квадратичного функционала:

Уравнения Эйлера-Лагранжа примут вид:

(11)

Граничные условия для этой задачи можно выбрать в следующем виде:

Каждое из последних уравнений системы (11) имеет решение:

Если идля всех, то из равенства (6) следует:

И система (11) принимает вид:

что соответствует случаю, когда на управление не накладывается ограничений.

Если же , из равенства (6) следует:

То есть управление достигает граничных условий.