Изопериметрическая задача

Это задача на условный экстремум.

Формулировка: Среди всех гладких кривых, которые удовлетворяют граничным условиям и условиям:

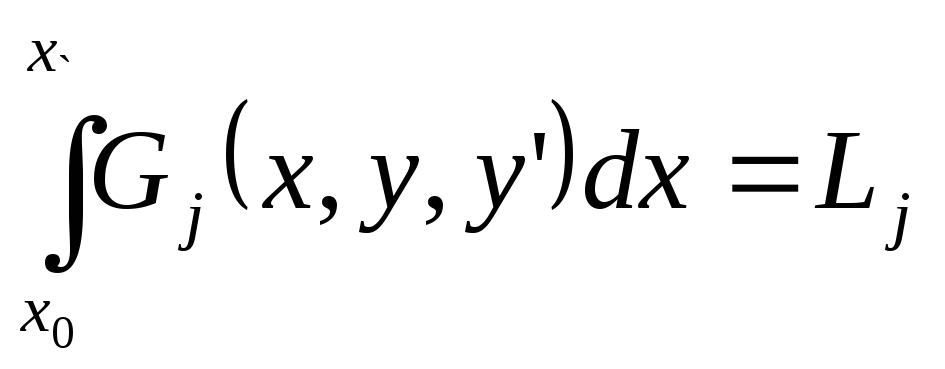
Требуется определить кривую, на которой достигается экстремум функционала:

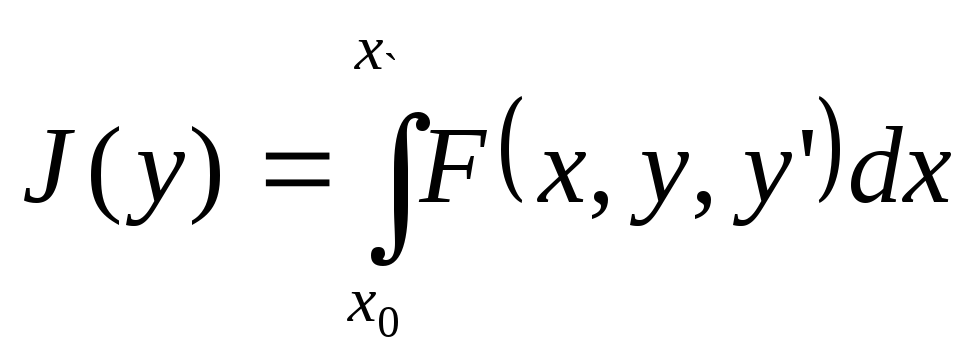
Изопериметрическая задача путем введения множителей сводится к задаче на безусловный экстремум следующего функционала. Из этого следует, что для решения изопериметрической задачи требуется составить уравнение Эйлера-Лагранжа для функционала вида 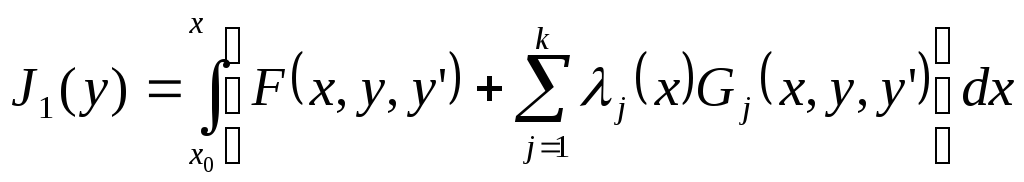(1):

(1)

Произвольные постоянные в общем решении уравнений Эйлера и определяются из граничных условий:

Задача Майера

Эта задача входит в класс задач на условный экстремум и формулируется следующим образом: Среди всех кривых, кусочно-гладких, которые удовлетворяют условиям связи:

(1)

и граничным условиям:

(2)

Требуется найти такую функцию, у которой первая составляющая имеет приэкстремум.

Задача Майера может быть сведена к задаче Лагранжа на условный экстремум, которая формулируется следующим образом: среди кусочно-гладких векторных функций , которые удовлетворяют уравнениям связи (1) и граничным условиям (2), требуется найти такую функцию, при которой функционал:

(3)

достигает экстремума.

В свою очередь путем введения новой функции:

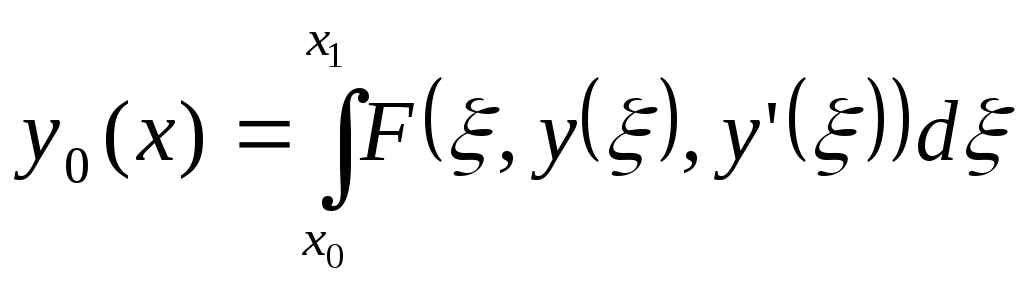
Задача Лагранжа может быть сведена к задаче Майера. Они эквивалентны.

Заменим вспомогательный функционал:

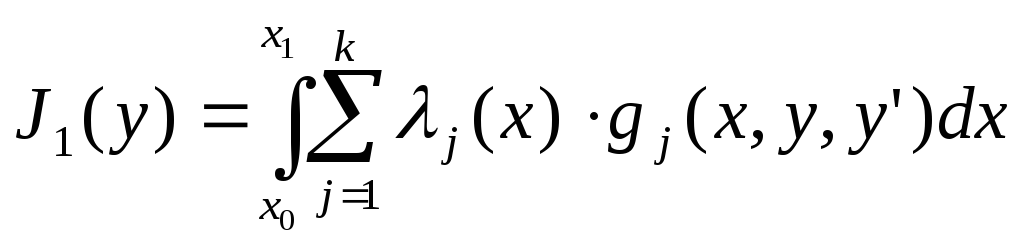(4)

Задача сводится к безусловному экстремуму, и уравнение Эйлера-Лагранжа для функции будет иметь вид:

(5)

Произвольные постоянные, возникающие при интегрировании уравнений (1) и (5) могут быть определены из условий (2). К уравнению (5) надо добавить kуравнений связи (1).

Задача Больца

В этой задаче необходимо определить кусочно-гладкую функцию, удовлетворяющую условию связей вида 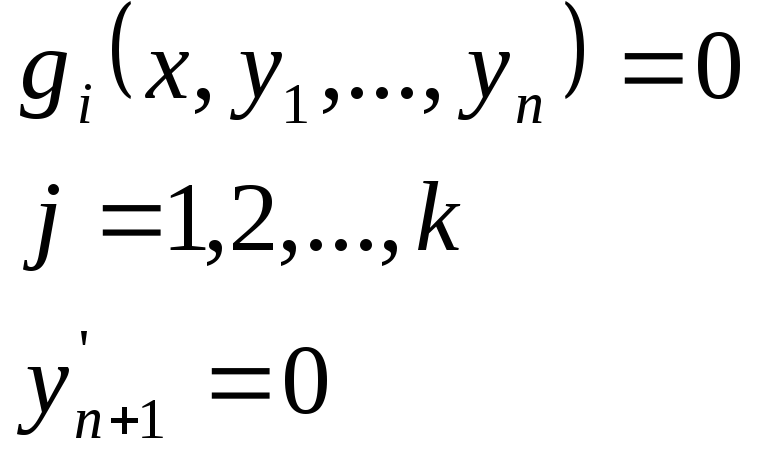(1):

(1)

Граничным условиям:

(2)

и доставляющую экстремум функционалу:

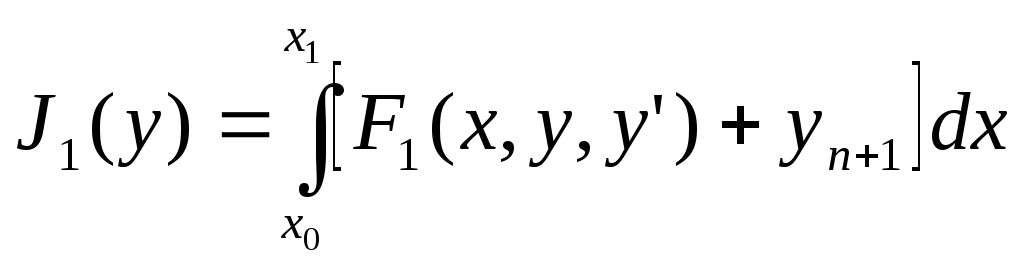(3)

Из уравнений связи следует, что , тогдаи, следовательно:

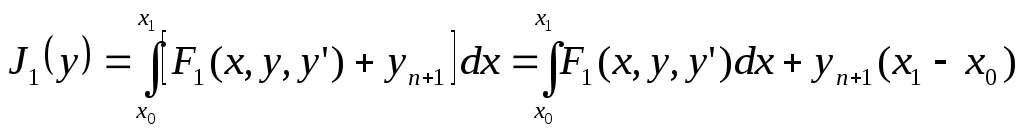
Из последнего равенства следует:

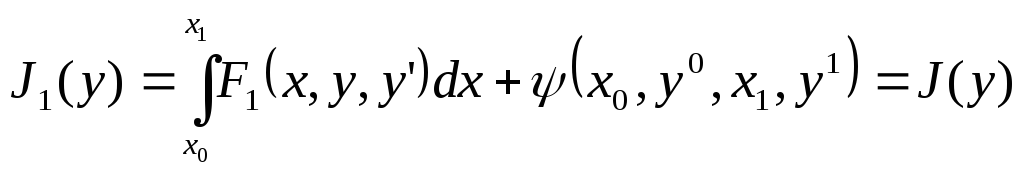
Здесь учтены граничные условия (2).

В свою очередь задача Лагранжа является частным случаем задачи Больца, когда:

.

Итак, если теперь ввести специальные множители , задача Больца также сводится к задаче на безусловный экстремум функционала:

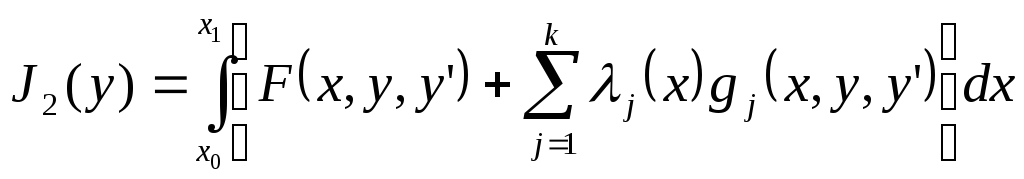(4)

Для определения неизвестных функций и множителей Лагранжанужно составить уравнение Эйлера-Лагранжа:

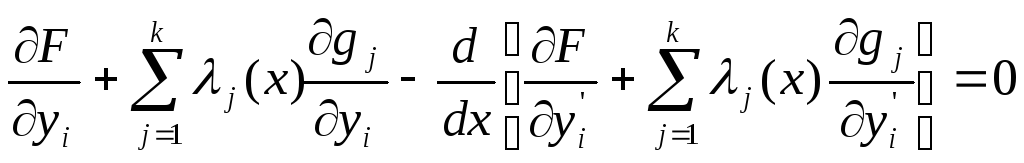(5)

которое удовлетворяет условиям связи:

Произвольные постоянные, которые возникают при интегрировании уравнения (5), могут быть найдены с помощью граничных условий (2).

Для граничных условий (2) необходимо использовать условие трансверсальности:

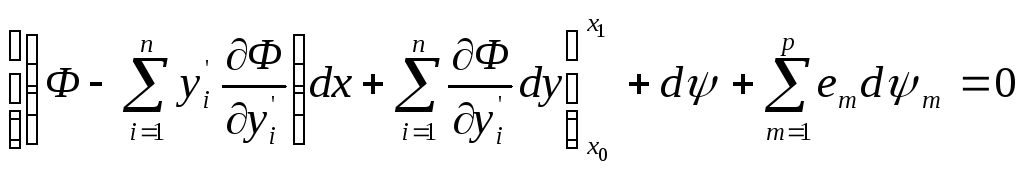(6)

Здесь:

Тождество должно иметь место для любых значений дифференциалов .

Линейные системы. Квадратичный критерий качества процессов управления

Будем считать, что объект управления описывается системой дифференциальных уравнений:

(1)

Здесь:

X–n-мерный вектор состояния ОУ;

U–m-мерный вектор управляющих функций;

A– матрица размера(матрица динамики ОУ);

B– матрица(матрица коэффициентов передачи).

Управление динамическим объектом (1) должно быть таким, чтобы минимизировать критерий качества ОУ в функционал:

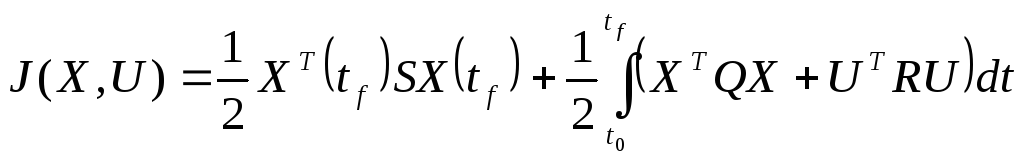(2)

Здесь ине отрицательно определенные симметричные матрицы размера, которые удовлетворяют условиям:

Эти два неравенства должны выполняться для любого n-мерного вектора.

Далее, - положительно определенная матрица, то есть это симметричная матрица, которая удовлетворяет условию:

для любого m-мерного вектора.

Мы считаем, что - начальное значение и- конечное значение вектора состояния ОУ.

Вводим в рассмотрение вспомогательный функционал:

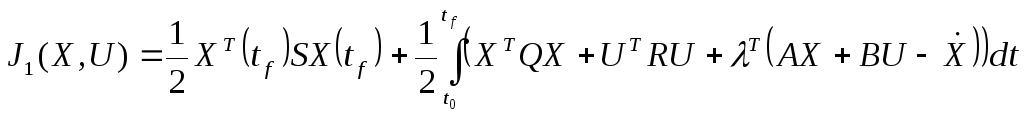(3)

Теперь вводится в рассмотрение вспомогательная скалярная функция:

(4)

Вводим вспомогательную функцию, которая имеет название – гамильтониан. В этом случае функционал запишется:

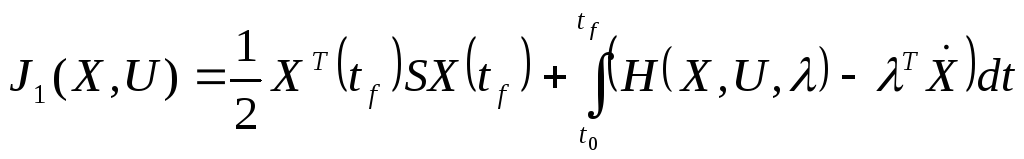(5)

Теперь рассмотрим интеграл: .

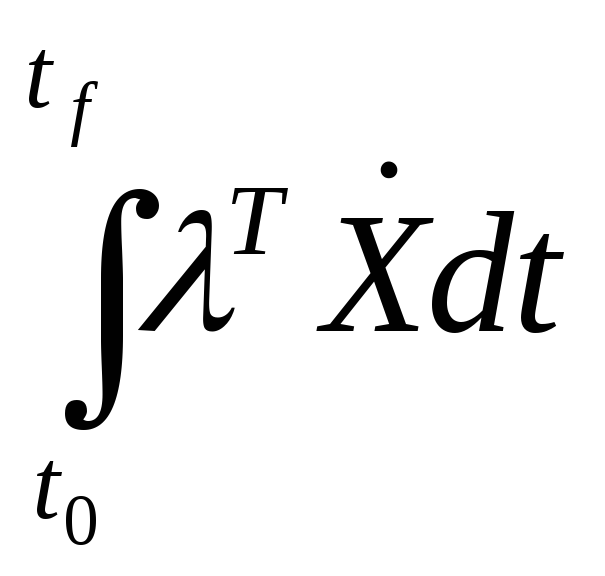Берем интеграл по частям:

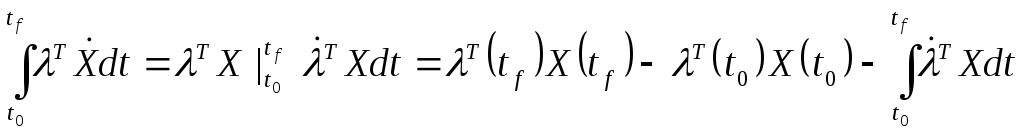
Теперь функционал (5) запишется в виде:

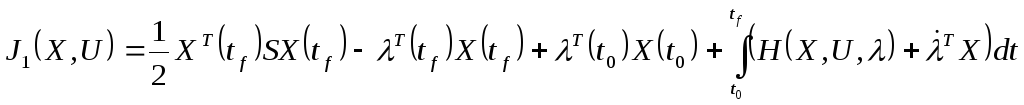(6)

Теперь рассмотрим вариацию этого функционала, которая вызвана вариацией управляющей функции и вектора. При этом считаем, что если начальное значение временификсировано, то фиксировано также и конечное значение времени.

Выражение для вариации функционала:

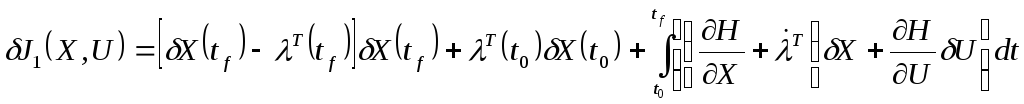(7)

Выберем вектортаким образом, чтобы коэффициенты при вариацияхибыли равны нулю. Тогда получаем уравнение для определения:

(8)

Граничные условия для системы уравнений (8):

(9)

Так как:

(10)

тогда в этом случае вариация функционала запишется:

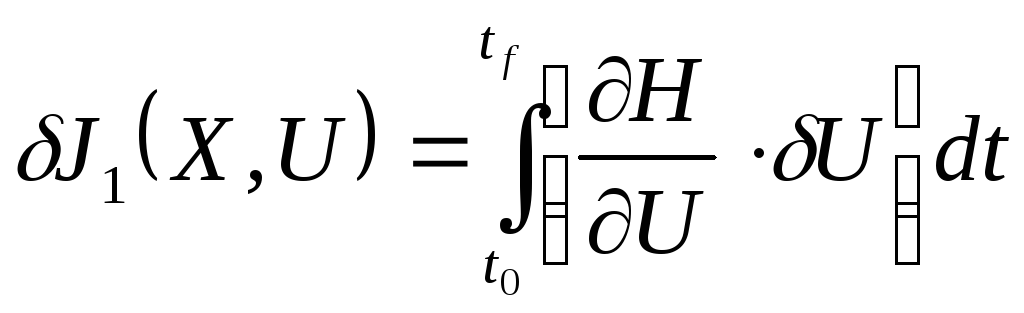(11)

Сделаем следующее замечание: вспомогательный функционал совпадает с исходным функционалом на решениях системы уравнений (1). Поэтому, еслидостигает минимума, то минимума достигает и функционал. Еслидостигает минимума, то его вариация должна быть равна нулю.

То есть должно выполняться условие:

(12)

Приведем сведения из линейной алгебры, которые мы будем использовать в дальнейшем:

На основании этих формул получаем следующее:

Чтобы найти вектор управляющих функций, которые доставляют экстремум функционалу (2) или критерию качества, нужно решить систему дифференциальных уравнений:

(13)

(14)

где управляющая функция определена из условия:

Транспонированный вектор управляющей функции определяется равенством:

Или:

(15)

Здесь следует отметить, что граничные условия для уравнений (13) и (14) разделены. Одно из них задано на левом конце траектории, другоезадано на правом конце.

Теперь, с учетом этого, запишем следующие дифференциальные уравнения, которые определяют оптимальное управление:

(16)

(17)

где заданы граничные условия:

и(18)

Это так называемая двухточечная краевая задача.