Стійкість лінійних систем.

Під стійкістю системи автоматичного керування розуміють здатність системи повертатися до сталого режиму після зникнення зовнішніх сил, які вивели її з такого стану.

Для визначення стійкості системи розроблені певні вимоги до параметрів математичної моделі (коефіцієнтів рівнянь, коренів рівнянь динаміки) та деяких характеристик системи керування. Вказані вимоги, які повинні задовольнятися в стійких системах, мають назву критеріїв стійкості.

Кореневий критерій стійкості.

Припустимо, що диференціальне рівняння динаміки замкнутої системи в операторній формі запису має вигляд

A(p)x(t)=B(p)f(t),

де x(t) - керована координата; f(t) - зовнішній вплив; A(р) і B(р) поліноми оператора диференціювання р.

Коефіцієнти полінома A(р) залежать тільки від параметрів основного замкнутого контуру керування, а коефіцієнти полінома B(р) - ще й від місця прикладення зовнішнього впливу.

Рішення лінійного неоднорідного диференціального рівняння з постійними коефіцієнтами представляється у вигляді суми двох складових

x(t)=х_в (t)+x_з(t),

де х_в(t) - вільна складова руху в системі, обумовлена загальним рішенням однорідного диференціального рівняння A(p)x(t)=0;

х_з - змушена складова руху, що виникає внаслідок наявності зовнішнього впливу f(t) і обумовлена частковим рішенням неоднорідного диференціального рівняння, вона визначає усталений рух у системі.

У стійкій системі по закінченню перехідного процесу наступає сталий режим, обумовлений змушеною складовою х_з, отже, вільна складова руху х_в(t) повинна прагнути до нуля, тобто . Рішення однорідного диференціального рівнянняA(р) х_в(t)=0 відшукується у вигляді:

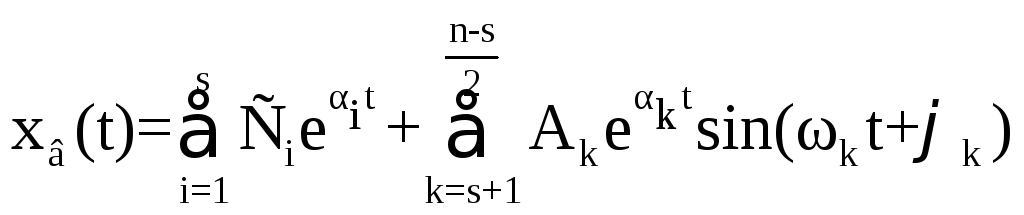
де n – ступень характеристичного рівняння М(р) = 0, загальна кількість коренів ;

s – кількість дійсних коренів ;

р_і=- дійсні корені характеристичного рівняння;

р_к= - комплексні корені;

C_i, А_k, - довільні постійні інтегрування.

Умова стійкості системи буде виконуватися лише прий, тобто коли дійсні корені та дійсні частини комплексних спряжених коренів характеристичного рівняння мають від’ємний знак.

Тобто ,необхідна умова стійкості полягає в тому, що в стійкій системі керування дійсні корені характеристичного рівняння та дійсні частини комплексних спряжених коренів мають бути від’ємними.

Якщо хоча б один корінь буде мати додатну дійсну частину, то відповідний йому член наведеної формули стане розбіжним й система виявиться нестійкою. Якщо відобразити розташування коренів на комплексній площині, то вони повинні розташуватися в лівій на півплощині відносно уявної осі. Уявну вісь, яка розмежовує області стійких та нестійких систем, називають межею стійкості.

Система керування (при відсутності додатних дійсних частин коренів характеристичного рівняння) може знаходитися на межі стійкості у двох випадках:

1. Якщо є хоча б один нульовий корінь (р₆), така система називається нейтральною. В такій системі може установити любе значення керованої величини.

2. Якщо є хоча б одна пара чисто уявних кореня (р_7,8) (з нульовою дійсною частиною), то в такій системі встановлюються незатухаючі коливання з постійною амплітудою. В такому випадку межа стійкості називається коливальною межею стійкості.

Теореми стійкості Ляпунова.

Розглянуті вище вимоги до розподілу коренів для забезпечення стійкості абсолютно застосовні до лінійних систем. Але ж реальні системи не є строго лінійними, лінійні характеристики ланок та їх лінійні диференціальні рівняння динаміки утворюються в результаті лінеаризації реальних рівнянь. При тому здійснюються певні спрощення (наприклад, відкидання членів вищого порядку малості), тому виникає питання, чи не зроблять суттєвого впливу на стійкість систем ті фактори, якими ми нехтуємо? Відповідь на це питання дають теореми Ляпунова.

1-а теорема. Якщо характеристичне рівняння лінеаризованої системи має усі корені з від’ємними дійсними частинами, то реальна система також буде стійкою, тобто врахування малих членів розкладення Тейлора не можуть порушити стійкість системи.

2-а теорема. Якщо характеристичне рівняння лінеаризованої системи має має хоча б один корінь з додатною дійсною частиною, то реальна система також буде нестійкою, тобто врахування малих членів розкладення Тейлора не можуть зробити систему стійкою.

3-а теорема. При наявності нульових або чисто уявних коренів характеристичного рівняння лінеаризованої системи поведінка реальної системи якісно не визначена. Врахування членів вищого порядку малості розкладення Тейлора можуть зробити реальну систему як стійкою, так і нестійкою.

Аналітичні критерії стійкості.

Необхідна умова стійкості.

Визначення коренів характеристичного рівняння без наявності необхідних технічних засобів іноді буває досить скрутно, тому потрібні якісь інші способи оцінки стійкості систем без знаходження коренів. Відомо, що корені характеристичного рівняння однозначно пов'язані з його коефіцієнтами, що надає можливість висунути певні вимоги до цих коефіцієнтів, задоволення яких має забезпечити стійкість системи керування.

Наприклад, для рівняння:

pⁿ₊ a_n-1p^n-1+………….+a₀=0

у відповідності до співвідношень Вієтта для дійсних коренів:

a_n-1=-(р₁+ р₂+ …….+ р_n);

a_n-2=р₁ р₂+ р₁ р₃+ …….+ р_n-1 р_n;

a_n-3=-(р₁ р₂ р₃+ р₁ р₂ р₄+ …….+ р_n-2 р_n-1 р_n);

.

.

a_n-2=(-1)ⁿр₁ р₂ р₃……. р_n .

Проаналізувавши наведені формули, неважко помітити, що в стійких системах при від’ємних значеннях усіх коренів (р_і0), усі коефіцієнтиa_i>0, іншими словами– для стійкості системи необхідно, щоби коефіцієнти характеристичного рівняння були додатними. Це твердження не має зворотної обов’язковості: додатність коефіцієнтів не свідчить про від’ємність коренів характеристичного рівняння системи, тому при додатних коефіцієнтах деякі корені можуть бути додатними, отже система буде нестійкою.

Вимога щодо знаків коефіцієнтів характеристичного рівняння справедлива не тільки для дійсних коренів, а і для загального випадку. Це можна обґрунтувати наступним чином.

Запишемо характеристичне рівняння для загального випадку:

a_npⁿ₊ a_n-1p^n-1+………….+a₀=0,

або

a_n(p- p ₁)( p- p ₂)…( p- p _n)=0,

де p ₁,p ₂,p ₃,…..,p _n–корені характеристичного рівняння. Будемо вважати, що a_n>0, що завжди можна забезпечити. Припустимо, що усі корені дійсні і, як потрібно для стійкості, від’ємні:

p ₁=-α₁, p ₂=-α₂, p ₃=-α₃,….., p _n=-α_n.

Тоді характеристичне рівняння матиме вигляд:

a_n(p+ α ₁)( p+ α ₂)…( p+ p _n)=0.

Якщо перемножити між собою двочлени, то жоден коефіцієнт отриманого рівняння не матиме знаку мінус. Це відповідає вже розгляданому вище випадку.

При наявності декількох пар комплексних спряжених коренів з від’ємною дійсною частиною, наприклад, p_k,k+1=-α_kjβ_k , кінцевого результату не змінить, тому що при перемноженні відповідних двочленів отримаємо:

(p+ α_k-jβ_k)∙(p+ α_k+jβ_k)=( p+ α_k)²+β_k²₌ p²+2рα_k+α_k²+ β_k².

Тобто, і у випадку наявності комплексних спряжених коренів з від’ємною дійсною частиною жоден з коефіцієнтів характеристичного рівняння не може бути від’ємним. Тому взагалі, необхідною умовою стійкості систем автоматичного керування є додатність усіх коефіцієнтів характеристичного рівняння. Для стійкості системи вимога додатності коефіцієнтів є необхідною, але не завжди є достатньою.

Для систем першого й другого порядку необхідна умова стійкості разом з тим є і достатньою. Для систем більш високого порядку окрім виконання необхідної умови потрібне виконання ще інших, додаткових, вимог. Для оцінки стійкості систем розроблені спеціальні критерії.

Алгебраїчні критерії стійкості.

Вперше задача знаходження критерію стійкості була поставлена Максвелом у 1868 році і була успішно розв’язана у 1873 році Раусом для рівнянь 4-ї і 5-ї степені, а вже у 1877 році повністю.

Критерій стійкості Рауса (без доказів).

Спочатку записують характеристичне рівняння у вигляді:

a_npⁿ₊ a_n-1p^n-1+………….+a₀=0,

У відповідності до алгоритму, запропонованого Раусом , складають таблицю, в якій у першому рядку записують коефіцієнти характеристичного рівняння через один, починаючи з коефіцієнта при старшій похідній. У другому рядку записують останні коефіцієнти те ж через один.

№ з/п	Допоміжна величина r0	Коефіцієнти характеристичного рівняння
		1	2	3	∙∙∙∙∙
1	—	an	an-2	an-4	an-6
2	—	an-1	an-3	an-5	an-7
3					∙∙∙∙∙
4					∙∙∙∙∙
5					∙∙∙∙∙
6	∙∙∙∙∙	∙∙∙∙∙	∙∙∙∙∙	∙∙∙∙∙	∙∙∙∙∙

∙∙∙∙∙ ∙∙∙∙∙ ∙∙∙∙∙ ∙∙∙∙∙ ∙∙∙∙∙

n+1

rn-2=

an+1,1=

an+1,2=

an+1,3=

∙∙∙∙∙

Для того, щоби система була стійкою, необхідно і достатньо, при додатності знаків усіх коефіцієнтів характеристичного рівняння, щоби знак першого стовпця був додатним, тобто : a_n>0; a_n-1>0; a₃₁>0; a₄₁>0; a₅₁>0 і т. д.

Складання таблиці, а особливо розрахунки досить трудомісткі і монотонні.

Критерій стійкості Гурвіца.

Формулювання критерію було виконане Раусом у1985 році на прохання словацького професора Стодоли. Для визначення стійкості системи керування необхідно скласти матрицю з коефіцієнтів характеристичного рівняння замкненої системи за нескладним алгоритмом. В першому рядку записують коефіцієнти через один, починаючи з другого, у другому рядку виписують коефіцієнти теж через один, починаючи з першого. Наступні рядки заповнюють коефіцієнтами, дотримуючи закономірність зміни індексів, при тому, якщо значення індексу перевищує n, або менше 0, то в відповідну комірку матриці записують 0:

an-1	an-3	an-5	an-7	……
an	an-2	an-4	an-6	……
0	an-1	an-3	an-5	……
0	an	an-2	an-4	……
0	0	an-1	an-3	……
0	0	an	an-2	……

Система автоматичного керування буде стійкою, якщо при виконанні необхідної умови стійкості (a_і>0), головний визначник матриці Гурвіца і всі його діагональні мінори додатні.

Критерій стійкості Вишнєградського.

Використовується тільки для систем 3 – го порядку, характеристичне рівняння якої має вигляд:

a₃p³₊ a₂p²+ a₁p+a₀=0.

Для стійкості систем 3 - го порядку необхідно і достатньо, щоби при додатності всіх коефіцієнтів характеристичного рівняння добуток середніх коефіцієнтів був більше добутку крайніх, тобто: a₃>0; a₂>0; a₁>0; a₀>0; a₁∙ a₂> a₀ ∙a₃.

Цей критерій є частковим випадком критерію стійкості Гурвіца, тому як визначник матриці Гурвіца має вигляд

,

то для стійкості системи потрібно щоби виконувалася вимога його додатності:

>0,

або:

,

що повністю співпадає з формулюванням критерію стійкості Вишнєградського.

Графічні критерії стійкості.

Критерій стійкості Михайлова.

З метою обґрунтування критерію, який був сформульований у 1936 році, розглянемо характеристичний поліном замкненої системи n – го порядку:

N(p) = a_npⁿ₊ a_n-1p^n-1+………….+a₀.

Підставимо в цей поліном p=jω.

N(jω) = a_n (jω) ⁿ₊ a_n-1 (jω) ^n-1+………….+a₀.

Виділимо в ньому дійсну та уявну частини:

N(jω) = X(ω) +jY(ω) = |N(ω)|∙e^jψ(ω),

де дійсна частина X(ω) = a₀- a₂ ω²+ a₂ ω²+ a₄ ω⁴- a₆ ω⁶…,

а уявна частина Y(ω) = a₁ω - a₃ ω³+ a₅ ω⁵- a₇ ω⁷+…,

модуль поліному |N(ω)| = ,

аргумент поліному φ(ω) = arctg.

Змінюючи параметр ω від 0 до ∞, побудуємо у комплексній площині множину векторів N(jω) і, поєднавши між собою їх кінці, отримаємо так званий годограф Михайлова.

Сформулюємо теорему:характеристичне рівняння не буде мати коренів у правій півплощині комплексної площини розміщення коренів характеристичного рівняння, якщо повний приріст аргументу ψ характеристичного поліному N(jω) при зміні ω від 0 до ∞, буде дорівнювати n∙π/2, де n – степінь полінома.

Запишемо характеристичний поліном N(jω) у вигляді:

N(jω) = a_n(jω – p₁) (jω – p₂) (jω – p₃) ∙∙∙(jω – p_n),

де р_і – корені характеристичного рівняння.

Кожен співмножник, що позначений у дужках, являє собою комплексне число. При перемноженні комплексних чисел їх модулі перемножуються, а аргументи додаються. Тому загальний кут повороту Δφ_N(ω) вектора N(jω) при зміні ω від 0 до ∞, дорівнюватиме сумі кутів повороту окремих співмножників Δφ_і(ω), що записані у дужках, тобто:

Δφ_N (ω) = Δφ₁(ω) + Δφ₂(ω) + Δφ₃(ω) + Δφ₄(ω) + ∙ ∙ ∙ + Δφ_n(ω).

Визначимо кути повороту окремих співмножників в залежності від типу коренів.

Нехай корінь р₁ є дійсне від’ємне число, р₁ = -α₁ (α₁>0). Перший співмножник характеристичного поліному N(jω) матиме вигляд (jω + α₁), тобто це є комплексне число з модулем |jω + α₁)| = та аргументом φ₁(ω) = arctg. При зміні ω від 0 до ∞ аргумент φ₁(ω) зміниться від 0 до π/2, тобто приріст аргументу даного співмножника Δφ₁(ω) = π/2- 0 = π/2.

Якщо припустити, що всі інші корені характеристичного рівняння теж є дійсними від’ємними числами, то загальний кут повороту вектора N(jω) дорівнюватиме Δφ_м(ω) = n∙π/2.

Припустимо, що корінь р₂ є дійсне додатне число, р₂ = α₂. Другий співмножник характеристичного поліному N(jω) матиме вигляд (jω – α₂), тобто це є комплексне число з модулем |jω – α₂)| = та аргументом φ₂(ω) = -arctg. У такому випадку при зміні ω від 0 до ∞ аргумент φ₁(ω) зміниться від 0 до (-π/2), тобто приріст аргументу даного співмножника Δφ₁(ω) = (-π/2)- 0 = - π/2.

З отриманого можна зробити висновок, що кожний дійсний від’ємний корінь збільшує загальний кут повороту вектора М(jω) на π/2, а кожний додатний корінь зменшує його на π/2.

Розглянемо вплив комплексних спряжених коренів з від’ємною та додатною дійсними частинами. Нехай 3-й та 4-й корені є комплексними спряженими з від’ємною дійсною частиною: р_3,4 = -α₃jβ₃, тому відповідні співмножники характеристичного поліному N(jω) матимуть вигляд (jω +α₃-jβ₃)∙(jω + α₃+jβ₃). Модулі кожного з співмножників дорівнюють |(jω +α₃-jβ₃)|= =, а |(jω + α₃+jβ₃)| =. Аргументи відповідно: φ₃(ω) = arctg, φ₄(ω) = arctg. При зміні ω від 0 до ∞ аргумент φ₃(ω) зміниться від γ₃ = arctg до π/2, φ₄(ω) від γ₄ = arctg до π/2, тобто загальний приріст аргументів обох векторів Δφ_3,4(ω) = Δφ₃(ω) + Δφ₄(ω) = = (π/2 - γ₃ )+ (π/2 - γ₄) = π/2 + arctg + π/2 - arctg = 2∙ π/2. Іншими словами, кожний з двох спряжених комплексних коренів з від’ємною дійсною частиною, як і один дійсний від’ємний корінь, збільшує загальний кут повороту вектора N(jω) на π/2. Неважко показати, що кожний з двох спряжених комплексних коренів з додатною дійсною частиною, наприклад для р_5,6 = α₅jβ₅, як і один дійсний додатний корінь, зменшує загальний кут повороту вектора N(jω) на π/2, тобто Δφ_5,6(ω) = - 2∙ π/2. Таким чином, наявність коренів з від’ємною дійсною частиною приводить до збільшення аргументу комплексного поліному N(jω) на величину π/2, а здодатноюдійсною частиною до зменшення на ту ж величину π/2.

Нехай кількість коренів характеристичного рівняння у правій на півплощині дорівнює l; завдяки їм, зміна аргументу дорівнюватиме -l∙π/2, решта (n-l) коренів, що знаходяться у лівій півплощині, змінять аргумент на величину (n-l)∙π/2.

Сумарний приріст кута:

Δφ_м(ω) = (n-l)∙π/2 + (-l∙π/2) = n∙ π/2 - l∙π,

Тобто якщо l = 0, то Δφ_м(ω) = n∙ π/2, що і потрібно було доказати.

Для стійкості системи автоматичного керування необхідно і достатньо, щоби вектор комплексного поліному N(jω), кінець якого при зміні ω від 0 до ∞ описує криву(годограф) Михайлова, мав кут повороту n∙ π/2.

Більш поширене інше формулювання критерію Михайлова: Для стійкості системи автоматичного керування необхідно і достатньо, щоби при зміні ω від 0 до ∞ годограф Михайлова пройшов послідовно у додатному напрямку n квадрантів.

При тому слід пам’ятати, що взагалі ω являє собою деякий штучний параметр, який за своєю фізичною суттю не є частотою.

На рисунку зображені криві Михайлова для різних за стійкістю систем керування 3 –го порядку. Як видно з рисунка, у відповідності до критерію стійкості Михайлова годограф 1 відповідає стійкій системі, 2 – нестійкій, а 3 та 4 – системам, які знаходяться на межі стійкості. Причому, значення ω, при якому годограф 3 проходить через початок координат, відповідає саме частоті незатухаючих коливань, характеристичне рівняння у даному випадку має принаймні одну пару чисто уявних кореня з нульовою дійсною частиною.

Увипадку, коли годограф починається з початку координат, характеристичне рівняння має один нульовий корінь (у характеристичному рівнянні відсутній вільний член).

Критерій стійкості Найквіста.

На відміну від попередніх випадків, критерій стійкості Найквіста дозволяє робити висновки щодо стійкості замкнених систем по вигляду АФЧХ розімкненої системи.

Будемо вважати, що функція передачі розімкненої системи має вигляд:

,

де N(p),M(p) –відповідно чисельник та знаменник функції передачі. При тому слід пам’ятати, що в мінімально фазових системах порядок чисельника m не перевищує порядку знаменникаn.

При підстановці р =jω в W(p) отримаємо комплексний коефіцієнт передачі

,

де U(ω), V(ω) – дійсна та уявна частини комплексного коефіцієнту передачі.

Якщо змінювати ω в межах -∞<ω<+∞, то отримаємо повну АФЧХ як дзеркальне відображення характеристик отриманих при зміні ∞ в межах -∞<ω<0 та 0<ω<+∞. Оскільки m≤n, то при частоті ∞→0 модуль W(jω) , буде наближатися до нуля, тобто АФЧХ розімкненої системи має закінчуватися в початку системи координат.

Сформулюємо вимоги до амплітудно-фазової частотної характеристики розімкненої системи, при виконанні яких cсистема автоматичного керування в замкненому стані буде стійкою.

Спочатку розглянемо стійкі статичні розімкнені системи, тобто такі, у яких корені характеристичного рівняння знаходяться у лівій півплощині.

Знаменник функції передачі замкненої системи керування F(р):

F(р)=1+W(p)=,

де М(р) – характеристичний поліном розімкненої системи,

D(p) – характеристичний поліном замкненої системи.

Зробимо заміну р=jω:

F(jω)=.

Варіюючи ω від -∞ до +∞, визначимо приріст аргументу

Δφ_F(ω)= φ_D(ω)-φ_M(ω).

Якщо всі корені характеристичного рівняння замкненої системи n – го порядку М(р)=0 знаходяться у лівій півплощині (система стійка), то, у відповідності до критерію стійкості Михайлова, загальний приріст аргументу характеристичного полінома замкненої системи φ_D(ω) повинен складати n∙π/2, тобто:

φ_D(ω)= n∙π/2.

Оскільки, як було умовлено, розглядаються стійкі системи у розімкненому стані, то загальний приріст аргументу характеристичного полінома розімкненої системи φ_M(ω) теж повинен складати n∙π/2, тобто:

Φ_M(ω)=n∙π/2.

Таким чином, загальний приріст аргументу комплексного полінома F(jω):

Δφ_F(ω)= n∙π/2- n∙π/2=0.

Це означає, що годограф F(jω) не повинен охоплювати початок координат.

АФЧХ W(jω) відрізняється від полінома F(jω) на 1. Тому краще користатися годографом амплітудно-фазової частотної характеристики розімкненої системи W(jω).

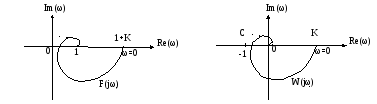
Розглянемо відображення на комплексній площині годографів F(jω) і W(jω). Як видно з рисунка, обидві криві ідентичні, якщо не враховувати зсув однієї з них по відношенню до початку координат на одиницю. На рисунках показано, що при ω=0 початкове значення обох кривих теж відрізняються на 1, при тому зрозуміло, що літерою К позначений коефіцієнт передачі розімкненої системи.

З рисунка випливає, що для того , щоби стійка система у розімкненому стані була стійкою у замкненому стані, необхідно і достатньо аби АФЧХ розімкненої системи W(jω) не охоплювала критичну точку С з координатами .

Якщо W(jω) проходить через точку С, замкнена система буде знаходитися на межі стійкості, це відповідає встановленню незатухаючих коливань. Цей факт випливає з того, що при перетині АФЧХ W(jω) точки С виконується рівняння:

W(jω) = -1+j0,

тому

1 + W(jω) = 0.

Тобто комплексний характеристичний поліном замкненої системи F(jω)=1+W(jω) дорівнює нулю. Якщо цей поліном можна записати у вигляді:

F(jω)=a_n(jω-p₁)( jω-p₂)…..( jω-p_n),

тому рівність нулю полінома можливе лише при наявності хоча б одного уявного кореня р_і з нульовою дійсною частиною, тобто р_і= jω, а це означає знаходження замкненої системи на межі стійкості.

Якщо розімкнена система знаходиться на межі стійкості, вимоги до АФЧХ розімкненої системи для забезпечення стійкості замкненої системи не змінюються, лише змінюється вигляд АФЧХ.

Визначимо вимоги до АФЧХ W(jω), якщо розімкнена система нестійка і lкоренів характеристичного рівняння знаходяться у правій півплощині.

Пам’ятаючи про те, l коренів, що розташовані у правій півплощині, при зміні ω від -∞ до ∞ дають приріст аргументу характеристичного полінома (- l∙π), а (n-l) коренів характеристичного рівняння, що знаходиться у лівій півплощині – (+n∙π), тому загальний приріст буде:

Δφ_F(ω)= φ_D(ω)-φ_M(ω)=n∙π-(( n-l) π-l∙π)=l∙2π.

Це означає, що для того, щоби нестійка у розімкненому стані система автоматичного керування була стійкою у замкненому стані, необхідно і достатньо аби крива F(jω) охоплювала початок координат у додатному напрямку l раз. По відношенню до АФЧХ розімкненої системи критерій Найквіста у такому випадку можна сформулювати таким чином:

Для того, щоби нестійка у розімкненому стані система автоматичного керування була стійкою у замкненому стані, необхідно і достатньо аби крива АФЧХ розімкненої системи W(jω) охоплювала критичну точку С з координатами l разів за напрямком годинникової стрілки.

Логарифмічний критерій стійкості.

У відповідності до критерію стійкості Найквіста, в стійких замкнених системах при значенні аргументу АФЧХ розімкненої системи φ(ω)=- π, значення модуля W(jω) повинне бути менше одиниці, тобто А(ω)<1, а логарифмічна амплітудно-частотна характеристика розімкненої системи (ЛАЧХ) L(ω)=20 lg А(ω)<0.

Якщо побудувати ЛАЧХ і ЛФЧХ для розімкненої системи, то неважко встановити їх взаємозв’язок, який забезпечує стійкість системи автоматичного керування у замкненому стані.

Будемо розглядати лише системи, які є стійкими у розімкненому стані.

На першому рисунку при частоті, при якій значення ЛФЧХ φ(ω) стає рівним –π, значення ЛАЧХ L(ω)>0. Це означає, що АФЧХ розімкненої системи перетинає дійсну вісь в інтервалі значень за межами , тобто охоплює критичну точку С, тому замкнена система буде нестійкою.

На другому рисунку при частоті, при якій ЛФЧХ φ(ω) відповідає тій же умові, ЛАЧХ L(ω)<0, тому АФЧХ розімкненої системи перетинає дійсну вісь в інтервалі значень від (-1) до 0, що відповідає стійкості замкненої системи керування.

Замкнена система керування буде абсолютно стійкою, якщо при частоті, при якій ЛФЧХ перетинає горизонтальну лінію –π, ЛФЧХ має додатне значення.

У випадку умовної стійкості вигляд ЛФЧХ має інший вигляд:

Частота, при якій ЛАЧХ перетинає вісь абсцис, називають частотою зрізу ω_зр, формулювання логарифмічного критерію стійкості змінюється:

Умовна стійкість забезпечується, якщо кількість перетинів ЛФЧХ φ(ω)значень –π до частоти зрізу ω_зр парне.

Нестійкі системи у розімкненому стані не розглядаються.

Особливості стійкості систем з запізненням.

При наявності в системі автоматичного керування елементів запізнення виникає необхідність визначення граничних значень часу запізнення, при яких система втрачає стійкість, оскільки такі ланки є джерелом збурень, що в істотній мірі впливають на фазові зсуви сигналів, отже на стійкість.

Розглянемо розімкнену систему автоматичного керування, яка містить ланку чистого (транспортного) запізнення:

Функція передачі такої системи

W(p) = W_o(p) ∙W_τ(p)= W_o(p) e^-pτ,

де W_о(p) –функція передачі частини системибеззапізнення,

W_τ(p)=e^-pτ–функція передачі ланки чистого запізнення,

τ – час запізнення.

Функція передачі замкненої системи має вигляд:

Φ(р)=.

Характеристичне рівняння замкненої системи:

=0.

Таким рівнянням можна користуватися для досліджень стійкості системи за допомогою будь-яких критеріїв. Але при аналізі характеристичного рівняння такого вигляду виникають певні математичні труднощі, тому більш зручним є використання критерію стійкості Найквіста, для якого не потрібно визначати функцію передачі для замкненої системи.

Комплексний коефіцієнт передачі розімкненої системи при наявності елемента чистого запізнення:

W(jω) = W_o(jω) ∙W_τ(jω)= А_o(ω) e^jφ(ω) А_τ(ω) e^-jωτ,

а оскільки значення амплітудно-частотної характеристики ланки чистого запізнення А_τ(ω) для всіх частот дорівнює одиниці, то:

W(jω) = А_o(ω) e^{j(φ(ω)-ωτ)}.

Аналізуючи отриманий результат, можна зробити висновок, що наявність ланки чистого запізнення не впливає на модуль вектора АФЧХ, але змінює фазовий зсув в напрямку руху годинникової стрілки на кут, що дорівнює –ωτ.

Розглянемо випадок, коли АФЧХ розімкненої системи перетинає коло одиничного радіуса в одній точці.

Позначимо літерою М точку перетину АФЧХ розімкненої частини системи W_o(jω), яка не має запізнення з колом одиничного радіуса. Ця точка відповідає конкретній частоті ω_м, при якій значення ФЧХ дорівнює φ(ω_м). Наявність в системі ланки чистого запізнення повертає вектор ОМ в напрямку руху годинникової стрілки на кут, величина якого залежить від значення часу запізнення. При деякому значенні цього часу τ_кр можливе виконання рівності:

φ(ω_м)- ω_мτ_кр=-π,

звідки τ_кр=.

Побудова областей стійкості. D-розбивка

При дослідженні САУ часто виникає необхідність встановити вплив параметрів системи на її стійкість. Для рішення цього завдання виконують побудову областей стійкості, тобто, областей значень параметрів при яких система є стійкою.

Розрізняють побудову областей стійкості в площині значень одного параметра й у площині двох параметрів.

Для побудови таких областей необхідно у просторі їхніх значень нанести лінії, що відповідають межі стійкості. Тоді область, обмежена цими лініями буде являти собою область стійкості.

При побудові областей стійкості можна використати будь-які критерії стійкості, як аналітичні, так і графоаналітичні.

У більше широкому плані поставлене завдання можна розглядати як окремий випадок виділення областей значень параметрів системи, які забезпечують однаковий розподіл коренів характеристичного рівняння в комплексній площині.

Області значень параметрів системи з однаковою кількістю коренів характеристичного рівняння в правій півплощині комплексної площини розподілу коренів називається D-областями, а сама розбивка простору значень параметрів називається D-розбиттям.

Якщо в правій півплощині комплексної площини розподілу коренів є l-корінь, то область значень для такого розподілу корінь позначається D(n-l), де n-порядок характеристичного рівняння, отже, загальна кількість коренів. Якщо всі n коренів перебувають у лівій півплощині (система стійка), то відповідна область значень параметрів системи для цього розподілу позначається відповідно D(n) і є областю стійкості. Загальна кількість D-областей n + 1: (D(n), D(n – 1), …....D (0)).

Для побудови D-областей, як вказувалося вище, можна користуватися будь-якими критеріями стійкості, але найбільш універсальним є приватний метод, запропонований. Соколовим О. О в 1940 р., який надалі був розвинутий в роботах Неймарка Ю. І.

D-розбиття по одному параметру.

Розбивка простору всіх значень деякого конструктивного параметра γ на області з однаковим розподілом коренів характеристичного рівняння в комплексній площині називається D-розбивкою по одному параметру.

Якщо необхідно з'ясувати, як впливає на стійкість САУ якийсь конструктивний параметр γ, що лінійно входить у коефіцієнт характеристичного рівняння замкнутої системи, то зазначене рівняння можна представити у вигляді:

Н (р) + γ G (р) = 0,

де Н (р) – многочлен, що не містить γ;

G (р) – многочлен, що є співмножником γ.

З цього рівняння знаходимо γ:

По фізичному змісту γ є дійсним числом, всі можливі його значення розташовуються на числовій осі (лінії). Побудова D-областей зручніше й наочніше проводити на площині, тому параметр γ краще розглядати як якесь комплексне число S =γ+ j λ, у якого дійсна частина γ по суті своїй є величиною, що досліджується.

Тому, після здійснення заміни р=јώ, одержимо γ у вигляді комплексного числа з дійсною частиною U (ω) і уявної V (ω):

γ = - = U (ω) + j (ω).

Для комплексного числа S:

γ = U (ω);

λ = V (ω).

Змінюючи значення ω від -до +, ­­можна розрахувати та відобразити  в комплексній площині величину S у вигляді кривої, яка поділить всю площину на декілька областей, серед яких може знаходитися і область стійкості.

Як конкретний приклад розглянемо систему автоматичного керування

структурна схема якої:

На схемі позначено:

у(р) - завдаючий вплив (завдання);

ε(р) – помилка керування;

μ(р) – керуючий вплив;

х(р) – керована величина;

Кп – коефіцієнт підсилення підсилювача;

Квм – коефіцієнт передачі виконавчого механізму;

Твм – постійна часу виконавчого механізму;

Коб – коефіцієнт передачі об'єкта;

Тоб – постійна часу об'єкта;

р - оператор Лапласа.

Функція передачі замкненої системи:

Ф (р) =

Характеристичне рівняння:

р (Твм р + 1)(Тоб р + 1) + Кп Квм Коб = 0.

Припустимо, що досліджується вплив коефіцієнта підсилення підсилювача Кп на стійкість САУ, тобто, γ = Кп, всі інші параметри відомі.

Розкривши дужки, одержимо:

Твм Тоб р³ + (Твм + Тоб) р² + р + Кп Квм Коб = 0.

Введемо запропоновані вище позначення:

Н (р) = Твм Тоб р³ + (Твм + Тоб) р² +р;

G (р) = Квм Коб

У нашому прикладі, після відповідної постановки одержуємо:

Н (jω) = - (Твм + Тоб) ω² + jω (1 - Твм Тоб ω²⁾;

G (jω) = Квм Коб;

γ = Кп =

де

U(ω) = V(ω) =

При зміні ω від -до +одержуємо числові значення U(ω) і V(ω), використовуючи які, будуємо відповідний графік у комплексній площині.

Отримана крива, що розмежовує всю комплексну площину на три області (I, II, III), називається основною кривою D-розбиття.

Якщо крива D-розбиття обмежує деяку область значень параметрів γ, при яких система стійка, то сама крива в площині параметра γ є межею стійкості.

У площині розподілу коренів характеристичного рівняння межею стійкості є уявна вісь, яку, з метою наочного відображення необхідного розташування коренів для забезпечення стійкості, за звичай штрихують ліворуч при зростанні значень ω на цій осі. Тому криву D-розбиття також варто заштрихувати ліворуч при збільшенні ω від -до +.

Із трьох отриманих областей тільки одна (I) має штрихування спрямоване усередину, тому саме для області I кількість корінь у правій напівплощині буде мінімальним; ця кількість може бути не рівною 0, тобто система буде нестійка.

Для оцінки, чи є область I областю стійкості, необхідно скористатися будь-яким критерієм стійкості при підстановці в характеристичне рівняння будь-якого значення γ у межах від γ₁ до γ_2. Якщо виявиться, що система стійка, то область I є областю стійкості. Перехід через криву D-розбиття із заштрихованої області в не заштриховану відповідає зменшенню кількості коренів у лівій півплощині на одиницю. В D-області I значення параметра Кп = γ обмежені точками перетину основної кривої D-розбиття з віссю абсцис. У цих точках λ = V(ω)=0, тому:

V(ω) = =0 при ω₁=0; ω_2,3 = ± ;

а отже:

γ₁ = Кп₁ = U(ω₁₎ = 0,

γ₂ = Кп₂ = U(ω_2,3) =.

У даному прикладі при зміні значень коефіцієнта підсилення підсилювача від Кп₁ до Кп₂ система стійка.

Визначення області стійкості, тобто D-розбиття по одному параметру, можна здійснити й іншими способами, наприклад, скориставшись будь-яким критерієм стійкості.

Так, у нашому прикладі характеристичне рівняння має вигляд:

р(Твм р+1)(Тоб р+1)+КпКвмКоб= Твм Тоб р³+ (Твм+Тоб) р²+ р+ КпКвмКоб= 0,

яке при Кп₁ = 0 перетвориться до виду:

р(Твм р+1)(Тоб р+1)=0.

Корені цього рівняння відповідно:

р₁=0; р₂ =<0; р₃=<0,

тобто два корені (р₂ і р₃) розташовані в лівій півплощині комплексної площини, а р₁ – на початку координат.

Очевидно, що при Кп₁ = 0 система перебуває на межі стійкості, це значення К_у1 є нижнім граничним значенням коефіцієнта підсилення підсилювача.

Верхнє граничне значення Кп₂ неважко визначити, скориставшись аналітичним критерієм Вишнєградського. Із цією метою розглянемо вищенаведене характеристичне рівняння.

Для системи 3-го порядку знаходження САУ на межі стійкості забезпечується при рівності добутків середніх і крайніх коефіцієнтів, тобто:

(Твм+Тоб)1=ТвмТобКп₂КвмКоб,

звідки:

Кп₂ =

Таким чином, при зміні Кп від 0 до значення система стійка, що повністю збігається з отриманим вище результатом D-розбиття при використанні частотного методу.

D-розбиття в площині двох параметрів.

Для побудови області стійкості в площині 2-х параметрів зручно скористатися критерієм стійкості Михайлова.

Будемо думати, що обоє досліджувані параметра μ і ν лінійно входять у коефіцієнти характеристичного полінома замкнутої системи.

F(p)=μМ(р) +νN(p)+Z(p)

Повертаючись до розглянутого приклада, припустимо, що досліджується вплив на стійкість САУ коефіцієнта підсилення підсилювача К_у й постійної часу об'єкта Т_об.

Характеристичний поліном розглянутої САУ має вигляд:

F(p)=Т_имТ_обр³+(Тім+Т_об)р²+р+К_уК_имК_об=Т_об(Т_имр³+р²)+К_уК_имК_об+р+Т_имр².

У цьому виразі можна прийняти позначення:

μ=Т_об; М(р) =Т_имр³+р²;

ν=К_у; N(р) =К_имК_об;

Z(р) =р+Т_имр²,

де μ і ν - параметри, вплив яких на стійкість САУ досліджується;

М(р) і N(p) - поліноми, що є співмножниками μ і ν відповідно;

Z(р) - поліном, що не містить ні μ, ні ν.

Здійснивши заміну р=jω, одержимо:

F(jω)= μ M(jω)+ ν N(jω)+Z(jω)=U(ω) +j(ω),

F (jω) є комплексним багаточленом, у дійсну U(ω) і уявну частину V(ω) якого лінійно входять параметри μ і ν.

У загальному вигляді дійсна й уявна частини можуть бути записані в такий спосіб:

U(ω)=μM₁(ω)+νN₁(ω)+Z₁(ω);

V(ω)=μM₂(ω)+νN₂(ω)+Z₂(ω);

Коливальній границі стійкості відповідає проходження годографа Михайлова через початок координат комплексної площини, тобто рівність нулю дійсної й уявної частин комплексного характеристичного полінома. Отже:

μM₁(ω)+νN₁(ω)+Z₁(ω)=0;

μM₂(ω)+νN₂(ω)+Z₂(ω)=0;

Визначення параметрів μ і ν здійснюють шляхом рішення системи рівнянь:

μ = ;ν = ,

де ;

;

.

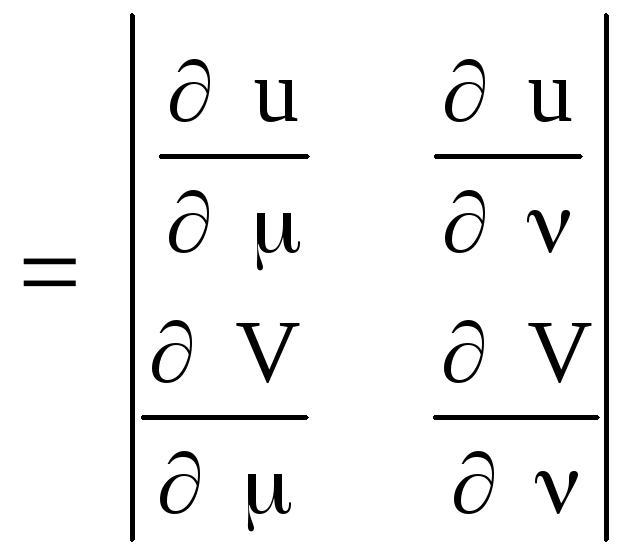У нашому прикладі, після підстановки р =jω, характеристичної поліном, з урахуванням того, що Т_об=μ, а К_у=ν здобуває вид:

F(jω)=μ(-jТ_имω³–ω²⁾ +νК_имК_об+(jω-тімω²⁾ =μ(-ω²⁾ +νК_имК_об–Т_имω²+j(μ(Тімω²)+ω);

U(ω)=μ∙ (-ω²⁾ +ν∙ К_имК_об–Т_имω²=0;

V(ω)=μ∙ ω(-Тімω²⁾ +ν∙ 0+ω=0,

де можна позначити:

M₁(ω) = -ω²; N₁(ω) = Кім К_об; Z₁(ω) = -Тім ω²;

M₂ (ω) = -Тім ω³; N₂ (ω) = 0; Z₂ (ω) = ω;

отже:

= Кім К_об Тім ω³;

= Кім К_об ω;

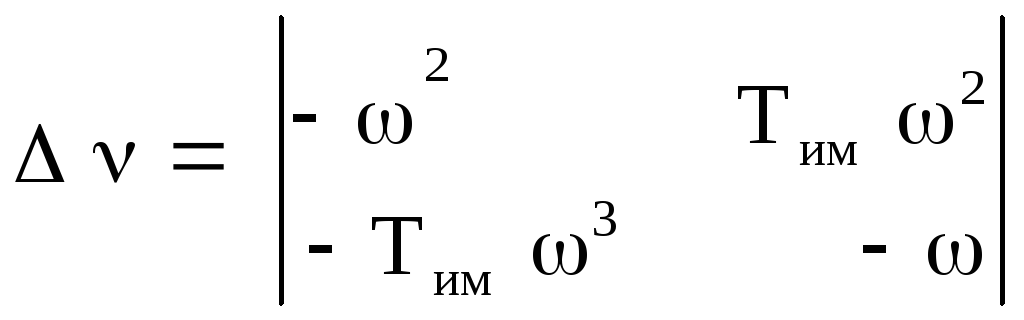=ω³+Тім²ω⁵=ω³(1+Тім² ω²⁾;

μ==;

ν = =;

Змінюючи ω від -до +, можна розрахувати й побудувати вплощині параметрів μ, ν основну криву D- розбивки, що є коливальною границею стійкості.

Основна крива доповнюється двома особливими прямими, рівняння яких виходять у результаті дорівнюючи до нуля коефіцієнтів при нульовій і старшій похідній характеристичного полінома,т.е:

Кім К_об · К_у= 0,

Тім Т_об = 0,

звідки:

К_у = ν = 0,

Т_об = μ = 0.

На малюнку представлена основна крива D-розбивки й дві особливі прямі співпадаючі з осями координат. Основна крива штрихується подвійним штрихуванням, оскільки обходиться двічі, будучи парною функцією ?.

Правила штрихування:

Спочатку штрихується основна крива D-розбивки, а потім особливі прямі.

Основна крива штрихується ліворуч при збільшенні ω від -до +, якщо> 0; аправоруч, якщо < 0. Оскільки при ω = 0 визначникміняє свій знак на протилежний, те основна крива обходиться двічі, отже двічі заштриховується;

Особливі прямі до крапки перетинання з основної кривої штрихуються одиночним штрихуванням таким чином, щоб їхні штрихування й штрихування основній кривій були спрямовані друг до друга або в різні сторони.

У розглянутому прикладі крива D-розбивки дозволяє відразу визначити область стійкості. Область, обмежена заштрихованими усередину лініями (область I) є областю стійкості, і це твердження не вимагає додаткової перевірки. Визначення зазначеної області здійснювалося, виходячи з первісного положення про те, що основна крива D-розбивки є границею коливальної стійкості й саме тому, відповідно до критерію стійкості Михайлова, речовинна й мнима частини характеристичного полінома прирівнювалися до нуля.

D-розбивка по двох конструктивних параметрах можна здійснити, використовуючи які-небудь інші критерії стійкості. Розглянемо можливість застосування критерію Гурвица.

У характеристичному рівнянні розглянутої як приклад системи

Т_имТ_обр³+(Тім+Т_об)р²+р+К_обК_имК_у=0

варьируемыми параметрами є =Т_об; =К_у, інші параметри фіксовані.

Система 3-го порядку, відповідно до критерію Вышнеградского, перебуває на границі стійкості при рівності добутків середніх і крайніх коефіцієнтів характеристичного рівняння, тобто:

(Тім+Т_об)1=К_обК_имК_уТ_имТ_об ,

звідки:

К_у==

Графік залежності К_у=f(Т_об), що представляє собою геометричну суму гіперболи й прямої лінії, паралельної осі абсцис, є основної кривої D-розбивки.

Рівняння особливих прямих, як і вказувалося вище, перебувають із умови рівності нулю коефіцієнтів при старшій і нульовій похідній характеристичного рівняння. У цьому випадку, рівняння особливих прямих перебувають із умов:

Т_имТ_об=0;

К_уК_имК_об=0,

звідки:

Т_об = μ = 0,

К_у = ν = 0.

Ці прямі збігаються з віссю ординат і віссю абсцис відповідно.

Для системи 3-го порядку такий підхід набагато простіше, ніж розглянутий вище, але при цьому виникають певні утруднення у виділенні області стійкості шляхом штрихування основної кривої D-розбивки й особливих прямих.