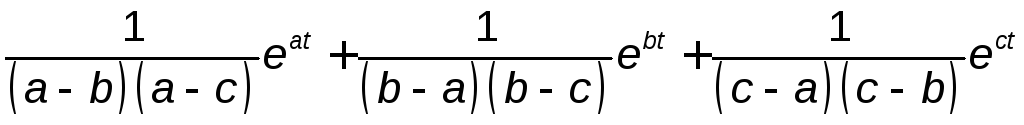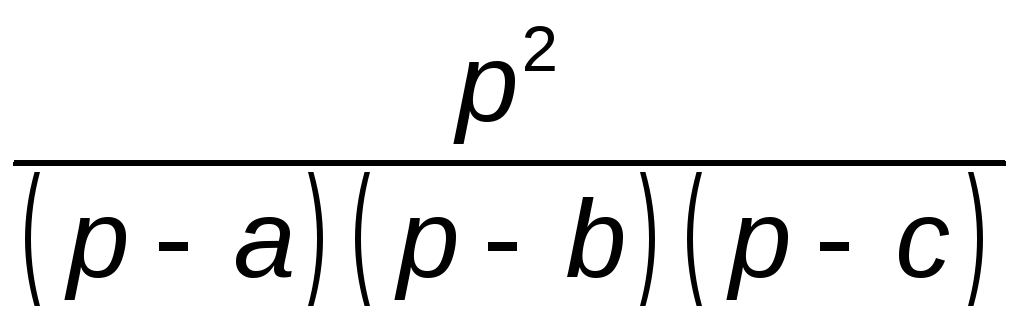Математичне моделювання лінійних систем керування.

Лінеаризація нелінійних диференціальних рівнянь динаміки САУ.

Математичний опис, необхідний для дослідження процесів керування, виконується у вигляді диференціальних, інтегральних або алгебраїчних рівнянь.

Динамічні процеси в інерційних системах й їхніх елементах описуються диференціальними або інтегральними рівняннями, що називають рівняннями динаміки, оскільки відбивають зміна в часі зміна координат стану елементів з урахуванням швидкості, прискорення й т.д. (1-я, 2-я … похідні).

Безінерційні елементи, як у перехідному, так й у сталому режимі, описуються алгебраїчними рівняннями, називаними рівняннями статики, оскільки відбивають стале співвідношення вхідних і вихідних величин.

Якщо параметри елементів зосереджені (у цьому випадку координати стани є як тільки функціями часу), то рівняння динаміки є звичайним диференціальним рівнянням. Системи з розподіленими параметрами описуються рівняннями в частинних похідних.

У загальному випадку диференціальні рівняння нелінійні, але при малих відхиленнях координат системи від стану рівноваги нелінійні рівняння можна приблизно замінити лінійними. Ця процедура заміни нелінійного рівняння лінійним називається лінеаризацією. Чим менше відхилення координат від стану рівноваги, тим точніше лінеаризоване рівняння описує реальний процес.

При складанні математичного опису будь-якої складної системи її попередньо представляють у вигляді сукупності окремих елементів взаємозалежних між собою, установлюють фізичний зміст вхідних і вихідних величин.

Розглянемо якийсь елемент системи автоматичного керування, на який впливають одночасно дві вхідних величини (х₁(t); х₂(t)), в результаті чого змінюється вихідна величина х₃(t).

Х₁(t)

Элемент САУ

Х₃(t)

Х₂(t)

Припустимо, що для розглянутого елемента складене диференціальне рівняння, що виявилося нелінійним.

.

Крапки над позначенням вхідних і вихідних змінних означають похідну, а їхня кількість - порядок похідній.

З огляду на складності аналізу нелінійних рівнянь, а також той факт, що в процесі керування всі вхідні й вихідні координати мало відхиляються від деяких сталих значень, лінеаризація представляється доцільної.

Допустимо, що сталий процес у системі має місце при деяких постійних значеннях х₁₀, х₂₀, х₃₀, тобто х₁(t)|₀=x₁₀; х₂(t)|₀=x₂₀; х₃(t)|₀=x₃₀, а .

Тоді, з огляду на те, що в сталому режимі всі похідні змінних дорівнюють нулю, рівняння приймає вид:

.

Позначимо значення змінних у динаміку:

х₁(t) = х₁₀ + Δх₁(t); = 0+Δ;

х₂(t) = х₂₀ + Δх₂(t); = 0+Δ;= 0+Δ;

х₃(t) = х₃₀ + Δх₃(t); = 0+Δ;= 0+Δ;= 0+Δ.

Розкладемо нелінійну функцію у кратний ряд Тейлора:

,

де Δх₁(t); Δх₂(t); Δх₃(t); - приріст відповідних змінних;

У рівнянні прийняті позначення виду , які варто розуміти як значення часткової похідної функції F по х при значеннях змінної х(t)|₀ у сталому режимі.

Віднімаючи рівняння сталого режиму і відкидаючи члени вищого порядку малості, одержимо:

Це рівняння, як і вихідне, описує той же динамічний процес у тій же системі керування. Всі часткові похідні являють собою постійні коефіцієнти, оскільки в них замість змінних підставлені їхні числові значення в сталому режимі. По суті, це рівняння являє собою суму перших ступенів різних змінних з відповідними коефіцієнтами. Таке рівняння є лінійним.

Відмінність його від вихідного нелінійного полягає в наступному:

Лінійне рівняння є наближеним , оскільки воно отримане в результаті відкидання в розкладанні Тейлора членів вищого порядку малості.

Невідомими функціями часу є не самі змінні х₁(t),х₂(t),х₃(t) і їхні похідні, а прирісти Δх₁(t), Δх₂(t), Δх₃(t) і т.д. Таке рівняння називається рівнянням у приростах (у варіаціях).

З отриманого виразу видно, що лінеаризація зводиться до одержання повного диференціала функції при заданих сталих значеннях змінних. Це можливо лише для функцій, що диференціюються, тобто таких, які у всіх точках мають кінцеві похідні. Функції, що не диференціюються, в такий спосіб лінеаризовувати не можна, існують інші способи лінеаризації, які будуть розглянуті далі.

Форми запису диференціальних рівнянь. Функція передачі.

Розглянемо простий варіант, у якому є одна вхідна величина х₁ й одна вихідна х₂.

Припустимо, що вихідне рівняння має вигляд:

.

У лінеаризованому вигляді:

Уведемо позначення постійних коефіцієнтів:

.

Після цього перейдемо до стандартної форми запису. Пам’ятаючи завжди, що рівняння динаміки записано у приростах, для більш стислої форми відкинемо позначку Δ:

Маючи на увазі, що х₁ є вхідною величиною, а х₂ – вихідною, у загальному виді рівняння може бути записано:

Диференціальне рівняння може бути записане в операторній формі:

де р = – оператор диференціювання.

Операторна форма не міняє його сутності, воно залишається диференціальним. У сталому режимі, коли х_вх = const, х_вих = const , p=, одержуєморівняння статики:

а₀х_вих = b₀х_вх,

звідки:

,

де k =– коефіцієнт передачі (посилення), що визначає крутість статичної характеристики.

Аналітичне рішення диференціальних рівнянь, особливо високого порядку, пов'язане з певними математичними труднощами, тому для полегшення цього завдання використовують спеціальні перетворення (наприклад, Лапласа або Карсона-Хевісайда), які дозволяють перейти від диференціальних рівнянь до алгебраїчних. При цьому у вихідних рівняннях здійснюється заміна реальних змінних і їхніх похідних відповідними зображеннями.

У вихідних рівняннях незалежної змінною є час t, а в їх зображеннях - комплексна змінна p=c+jω.

Пряме перетворення Лапласа, тобто перехід від оригіналу до зображення здійснюється за допомогою інтеграла Лапласа:

.

Для багатьох функцій існують таблиці перетворень Лапласа (див. відповідну таблицю).

Формули прямого і оберненого перетворення за Лапласом

№ п/п	Оригінал	Зображення
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

Практичний перехід від диференціальних рівнянь до їхніх зображень по Лапласу здійснюється без яких-небудь обчислень. Формально, при нульових початкових умовах, перетворення здійснюється шляхом заміни оригіналів функції х(t) їхніми зображеннями Х(р), а символів диференціювання позначенням оператора Лапласа рⁿ. Операція диференціювання оригіналу функції відповідає операції множення її зображення на комплексне число р:

,

операція інтегрування оригіналу функції відповідає операції поділу її зображення на р:

.

З огляду на вищесказане, запишемо вихідне рівняння, використовуючи перетворення Лапласа:

.

Така форма запису називається операційною формою. Рівняння в операційній формі по природі є алгебраїчним, рішенням такого рівняння є зображення змінної у часі величини, а не сама величина.

Рішенням алгебраїчного рівняння є зображення по Лапласу вихідної величини:

.

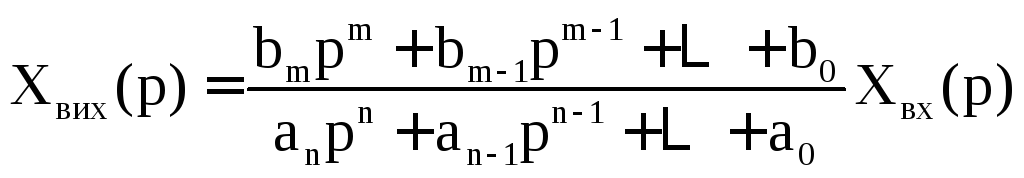Для визначення оригіналу можна скористатися або таблицями зворотних перетворень, або шляхом обчислення відповідного інтеграла зворотного перетворення Лапласа:

.

Дріб, що знаходиться в правій частині зображення по Лапласу вихідної величини, являє собою відношення зображень вихідної і вхідної величин (при нульових початкових умовах), називається функцією передачі W(p).

.

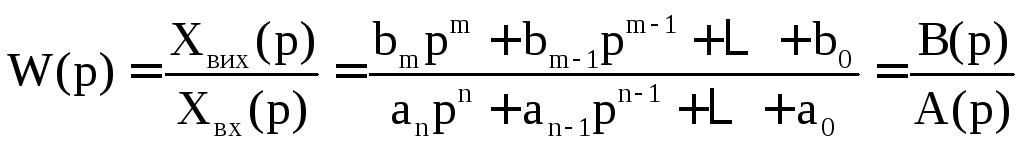Знаменник функції передачі прирівняний до нуля називається характеристичним рівнянням:

,

воно визначає перехідну складову протікання процесу. У сталому режимі, тобто при р=0, функція передачі W(0) чисельно дорівнює коефіцієнту передачі k:

.

Статичні і динамічні і характеристики.

Рівняння статики відбиває в аналітичній формі зв'язок між вихідною й вхідною величинами в сталому режимі, яке можна отримати шляхом підстановки в рівняння динаміки значення р=0.

Графічне зображення залежності вихідної величини від вхідної в сталому режимі називається статичною характеристикою.

Перехідною функцією h(t) називається аналітичний опис зміни вихідної величини у часі при одиничній стрибкоподібній зміні вхідної величини при нульових початкових умовах. Перехідна функція відбиває реакцію елементу або системи в цілому на одиничний ступінчастий вплив при нульових початкових умовах, що по суті являє собою перехідний процес, який виникає в елементі при одиничному стрибку сигналу на вході (х_вх(t) = 0 при t0; х_вх(t) = 1 при t > 0).

Перехідна функція може бути отримана шляхом рішення диференціального рівняння класичним методом або, використовуючи перетворення Лапласа, операційним методом.

Для визначення зображення по Лапласу вихідної величини операційним методом в рівняння

Х_вих(р) = W(p)Х_вх(р)

замість Х_вх(р) треба підставити зображення по Лапласу одиничного стрибка L та вираз функції передачі

.

Оскільки за визначенням зображення по Лапласу перехідної функції H(p) і є зображення по Лапласу вихідної величини Х_вх(р) при одиничному стрибку, то

.

Оригінал перехідної функції h(t) можна визначити по відповідним таблицям зворотного перетворення Лапласа або користуючись теоремою розкладення. В останньому випадку послідовність визначення полягає в наступному.

В загальному випадку, при відсутності нульових полюсів, H(p) має вигляд дробно-раціональної функції:

де - чисельник зображення по Лапласу перехідної функції H(p);

- знаменник зображення по Лапласу перехідної функції H(p).

В такому випадку перехідну функцію можна визначити за основною формулою теореми розкладення:

де n – степінь поліному ;

–корені характеристичного рівняння ,;

=- похідна знаменника зображення по Лапласу перехідної функції H(p).

В випадку однократного нульового полюса зображення за Лапласом перехідної функції має вигляд дробу:

Оригінал перехідної функції можна визначити за додатковою формулою теореми розкладення:

Перехідна характеристикає графічним відображенням перехідної функції h(t) , являючи собою графічне зображення зміни вихідної величини у часі при одиничній стрибкоподібній зміні вхідної величини.

Окрім перехідної характеристики існує ще імпульсна характеристика. Вона являє собою реакцію елементу або системи керування в цілому на вхідний імпульс необмеженої величини при нульовій його тривалості (δ-функція). Теоретично δ-функція дорівнює похідній одиничного стрибка δ(t)=, а площа імпульсу дорівнює одиниці, тобтоS =

Аналітичний вираз, по якому будується імпульсна характеристика, називається функцією ваги w(t). Між функцією ваги w(t) і перехідною характеристикою h(t) існує однозначний взаємозв’язок:

а функція передачі W(p) являє собою пряме перетворення Лапласа функції вагиw(t)

.

Частотні характеристики.

Для оцінки частотних властивостей елементів і систем широко використовуються так звані частотні характеристики.

Розглянемо систему керування, рівняння динаміки якої записано в операторній формі:

а_nрⁿх_вих(t)+ а_n-1р^n-1х_вих(t)+…….+ а₀х_вих(t) = b_mp^mx_вх(t)+ b_m-1p^m-1x_вх(t)+…….+ b₀x_вх(t)

Нехай на вхід системи поданий гармонічний сигнал х_вх(t) = А_вхSinωt.

Після закінчення перехідного процесу на виході системи керування встановляться теж гармонічні коливання з тією ж частотою, але з іншою амплітудою і зсунуті по фазі на кут φ відносно вхідного впливу:

х_вих(t) = А_вих sin (ωt+φ(ω)),

де А_вх, А_вих – амплітуди вхідного та вихідного сигналів відповідно;

φ(ω) – кут зсуву по фазі вихідного сигналу, який залежить від частоти вхідного сигналу.

Використаємо комплексну форму запису:

х_вх(t) = А_вхe^jωt;

х_вих(t) = А_вих e^{(jωt+φ(ω))}.

Підставимо ці значення в операторну форму диференціального рівняння, враховуючі при цьому, що е^{j(ωt+φ(ω))} = е^jωt е^jφ(ω); р^к(А_вхе^jωt) = (jω)^кА_вхе^jωt; р^к(А_вихе^{j(ωt+φ(ω))}) = (jω)^кА_вихе^jωt е^jφ(ω):

(а_n(jω)ⁿ+ а_n-1(jω)^n-1+…….+ а₀) А_вихе^jωt е^jφ(ω) = (b_m(jω)^m+ b_m-1(jω)^m-1+…….+ b₀) А_вхе^jωt

звідки:

.

Неважко побачити, що права частина являє собою функцію передачі, в якій зроблена підстановка р = jω. Оскільки ця величина являє собою комплексне число, то його можна записати у вигляді:

W(jω) =

Вираз W(jω) називають комплексним коефіцієнтом передачі, або комплексною функцією передачі. Як кожну комплексну величину, її можна представити або в декартовій, або полярній системі координат.

Графічне відображення комплексного коефіцієнту передачі комплексній площині називають амплітудно-фазовою частотною характеристикою:

W(jω) = P(ω) + jQ(ω),

де P(ω) – дійсна частина;

Q(ω) – уявна частина.

Для полярної системи

W(jω) = ,

де А(ω) – коефіцієнт передачі системи на частоті ω, за своєю сутністю є модулем комплексного коефіцієнта передачі W(jω):

А(ω) ===,

Зсув по фазі φ(ω) є аргументом комплексного коефіцієнту передачіW(jω):

φ(ω) = arg(W(jω)) = arc tg.

Г

φ(ω)

рафічне зображення залежності коефіцієнта передачі А(ω) від частоти називається амплітудно-частотною характеристико (АЧХ) , а залежності зсуву по фазі φ(ω) вихідного сигналу від частоти – фазово-частотною характеристикою (ФЧХ).

Обидві частотні характеристики можна побудувати в логарифмічних координатах. При побудові логарифмічної амплітудно-частотної характеристики (ЛАЧХ) по осі абсцис відкладають логарифм частоти в декадах, а по осі ординат L(ω)= 20 lg A(ω) в децибелах. Для логарифмічної фазово-частотної характеристики (ЛФЧХ) по осі ординат відкладають значення фази в радіанах або в градусах.

П

lgω, дек

ід декадою розуміють масштабний відрізок на осі, співвідношення частот на кінцях якого дорівнює 10.

В теорії автоматичного керування іноді використовують побудову залежностей дійсної P(ω), а також уявної Q(ω) частин комплексного коефіцієнту передачі від частоти, отримуючи таким чином дійсну частотну та уявну частотну характеристики ДЧХ і УЧХ. ДЧХ в свій час була дуже поширена, оскільки являлася основою для побудови перехідних характеристик систем керування завдяки однозначному її зв’язку з перехідними процесами. З розвитком сучасних засобів обчислювальної техніки та числових методів рішення диференціальних рівнянь використання ДЧХ дещо зменшилося.