Лекция 7.Оценивание вектора состояния.

Обычно не все компоненты вектора состояния доступны для измерения либо из-за ограниченного числа измерительных устройств, либо из-за невозможности измерения некоторых координат состояния. Как правило, измеряемыми выходными переменными объекта являются отдельные компоненты вектора состояния или их комбинации.

Простейшим способом восстановления вектора состояния является дифференцирование (n-1) раз измеряемых величин входа и выхода. Однако «чистое» дифференцирование практически трудно осуществимо и построенное таким образом устройство состояния (УСО) будет чувствительным к различного рода помехам.

При оптимизации динамических объектов, а также при построении адаптивных систем управления, ставится задача определения оценки вектора состояния на базе измеряемых входных и выходных переменных и структуры объекта. Задача может быть решена различными методами теории наблюдения, основанной на введенном Калманом понятии наблюдаемости.

Одна группа методов предусматривает восстановление текущего значения вектора состояния динамическим наблюдающим устройством, называемым индикатором состояния, непрерывно формирующим оценку вектора состояния по некоторым непрерывно измеряемым координатам состояния.

Другая группа методов использует для восстановления векторов состояния в определенный момент времени результаты наблюдения за измеряемыми координатами на интервале времени . В этом случае решение задачи наблюдения основывается на использовании понятия «отображения наблюдаемости», поэтому устройство восстановления вектора состояния называют наблюдаемым.

Методы оценки вектора состояния достаточно хорошо разработаны для линейных объектов; для нелинейных же динамических объектов имеется только ряд частных решений.

Рассмотрим способ построения УСО для стационарного линейного объекта, заданного нормализованными уравнениями состояния типа:

где матрицы А, В и С известны.

УСО можно построить в соответствии с уравнением математической модели объекта (1)

который формирует оценку , если на его вход поступает то же управляющее воздействие U(t), что и на объект без измерений выходного сигнала.

Размерность ОСУ, определяемая (2), равна размерности объекта. Если совпадают начальные состояния УСО и объекта , то в любой момент времени t. Однако выбор начального состояния УСО в каждый момент времени, когда оно используется, представляет собой самостоятельную задачу, которая может быть решена только для полностью идентифицируемого объекта, по известным значениям входа и выхода.

Чтобы устранить указанные недостатки, на вход УОС, кроме сигнала управления подают сигнал рассогласования между выходом объекта и его оценкой . Для построения таких УОС используют обратную связь по выходу объекта, а вместо уравнения (2) принимают уравнение

(3) ,

где - некоторый вектор, компоненты которого выбирают так, чтобы обеспечить желаемый процесс оценивания вектора состояния и получить

(4) ,

Построенные в соответствии с (3) и (4) УОС являются асимптотически устройствами оценивания вектора состояния и имеют ту же размерность, что и объект.

Уравнение (3) можно записать в виде

(5) .

Если при этом собственные числа матрицы выбраны за счет вектора так, что их вещественные части отрицательны, то для любых начальных состояний УОС при . Чем больше модули вещественных частей собственных чисел , тем быстрее оценка стремится к действительному значению вектора состояния.

Для наблюдаемого объекта можно построить n - мерной асимптотическое устройство УОС с заданным качеством процесса восстановления вектора состояния. Чтобы УОС выполняло поставленную задачу с заданным качеством, для его построения вместо (5) используют преобразованное уравнение вида

(6) ,

(6а) где ; ; .

Р - матрица линейного преобразования, выбираемая так, чтобы матрицы и имели идентификационное каноническое представление

;

(6б)

При выборе элементов вектора используется формула

(7) ;

где - коэффициенты многочлена , соответствующего заданному качеству процессов УОС.

(8)

n - порядок многочлена (порядок объекта).

В рассматриваемом случае характеристический многочлен матрицы и совпадают.

Если объект имеет координат управления, то в уравнении (3) вместо вектора записывают матрицу размерности и ее элементы выбирают из условия совпадения характеристического многочлена матрицы и заданного многочлена с коэффициентом (см. (8)).

Пример.

Построим асимптотическое УОС для объекта, динамика которого определяется уравнением

(9)

Запишем уравнение состояния, соответствующее (9)

(10)

В данном случае матрицы

(11) ; ;

таковы, что объект полностью управляем и полностью наблюдаем, так как ранги матрицы управляемости и наблюдаемости имеют соответственно значения

;

;

Следовательно, объект, описываемый уравнением (10), является идентифицируемым.

Чтобы привести матрицы объекта (11) к идентификационному каноническому представлению примем матрицу преобразования Р и соответствующую ей обратную матрицу Р^-1(при нормализированных уравнениях состояния, матрица Р является перестановочной)

(12) ; .

Тогда на основании 6а получим:

; ; .

Элементы вектора определим для заданного полинома по формуле (8)

;

так как .

Таким образом, соответственно (6), а также полученным значениям матриц , , и вектора запишем уравнение УОС в виде

(13)

Ниже приведена структурная схема асимптотического УОС второго порядка, соответствующая матричному уравнению (13).

Для реализации данного УОС дифференциаторы уже не нужны, а необходимы лишь интеграторы и усилители.

Существует метод построения асимптотических УОС, порядок которых меньше порядка объекта на число линейно независимых измеряемых выходов объекта. Такие упрощенные устройства иногда наблюдателями или идентификаторами Луенбергера. Для объектов n - ого порядка с одним выходом наблюдатель Луенбергера имеет (n-1) - й порядок.

Для построения упрощенных УОС (n-1) - ого порядка используют уравнения вида

(14)

где - матрица, определяется матрицей в результате замены элементов последнего столбца и последней строки нулями; - последний столбец матрицы , последняя компонента которого принята равной единице; - столбец матрицы , последняя компонента которого принята равной нулю.

Матрицы и определяются как

(15) ;

причем I - единичная диагональная матрица размерности , - коэффициенты многочлена (n-1) - ого порядка

(16)

Выходную переменную объекта используют в упрощенном УОС в качестве оценки n - й компоненты вектора состояния или , где . Поэтому упрощенное УОС имеет меньшее количество элементов, чем асимптотическое УОС, построенное по уравнению (5). Если объект имеет несколько измеряемых переменных, например, р, то упрощенное УОС может иметь порядок (n-p) и оценивать все компоненты вектора состояния.

Пример.

Построим упрощенное УОС (n-1) - ого порядка для объекта, заданного уравнениями

(17)

В данном случае матрицы

(18) ; ;

таковы, что объект полностью управляем и наблюдаем, так как соответственно

;

;

Следовательно, объект идентифицируем.

Динамику упрощенного УОС первого порядка задаем характеристическим многочленом

Преобразуем (18) к идентификационному каноническому виду с помощью матриц Р и Р^-1вида (12), тогда

; ; .

В соответствии с (15) получим

;

; ;

; ; .

На основании (15) и полученных значений  , , запишем матричное уравнение упрощенного УОС для данного объекта:

(19)

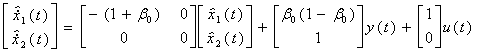
Ниже представлена структурная схема устройства, соответствующего уравнению (19).

Это упрощенное устройство УОС имеет меньшее количество элементов, чем устройство, представленное ранее, оценивающее вектор состояния объекта также второго порядка.

60