Лекция № 3. Уравнения состояния элемента автоматической системы
Уравнением состояния элемента автоматической системы называют равенство, связывающее входную и выходные величины, изменяющиеся во времени, и справедливое для любого момента времени.
Известно, что любую величину, изменяющуюся во времени можно представить в виде
(2.43)
Представим в таком виде величину, поданную на вход элемента
Тогда величину на выходе элемента в том же виде можно изобразить так:
Считая, что в каждое мгновение времени в элементе наступает состояние равновесия, можно это состояние всякий раз описывать уравнением
или
Это уравнение и называют нормальным уравнением состояния элемента автоматической системы. Очевидно, что то же уравнение можно записать в более общем виде.
(2.45)
Такой вид уравнений состояния элемента обычно называют общим. Уравнение общего вида легко привести к нормальному:
(2.46)
В этих уравнениях
коэффициент передачи элемента:
постоянные времени объекта:
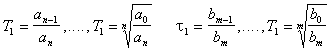
Коэффициент передачи и постоянная времени однозначно характеризуют свойства элемента и в большинстве случаев являются постоянными величинами и называются параметрами элемента автоматической системы.
Если элемент работает в рабочей точке Х, У , то его состояние в установившемся режиме опишется уравнением статики.
(2.47)
*
При выходе из установившегося состояние координаты элемента получат приращение и станут равными
а уравнение такого состояния элемента будет иметь вид
**
или поскольку производные от постоянных величин равны нулю
Очень удобно вести отсчет координат с рабочей точки /т.е. перенести начало координат в рабочею точку /, так как при этом начальные условия в большинстве случаев становятся нулевыми, Для получения уравнения состояния в этой системе отсчета необходимо из уравнения состояния - вычесть уравнение статики.
В результате получим
Это уравнение обычно называют уравнением состояния элемента в приращениях от рабочей точки.
При выводе уравнения состояния можно производить в следующем порядке.
1. Определяются обобщенные координаты Х и У элемента 2. Явления преобразования Х в У разделяются на простейшие преобразования
3. Каждое простейшее преобразование / явление / на основании физических, химических и т.п. законов описывается уравнением. 4. Полученная таким образом система уравнений решается относительно обобщенных координат. 5. Окончательное уравнение приводится к нормальному виду
Если в процессе вывода будут получаться нелинейные зависимости, они линеаризуются одним из рассмотренных ранее способов
Пример.
Вывести уравнение состояния генератора постоянного тока с независимым возбуждением.
1. Состояние генератора постоянного тока в любой момент времени определяется напряжением возбуждения U скорости вращения якоря n и ЭДС на щетках якоря.
Примем, что во время работы скорость вращения якоря остается постоянной, тогда за обобщенные координаты можно принять U и Е, т.е. схематично генератор можно представить в виде
2. Преобразования напряжения возбуждения в ЕДС происходит так:
напряжение U в обмотке возбуждения преобразуется в ток I, который в магнитной системе генератора создает магнитный поток Ф, а последний во вращающейся обмотке наводит ЕДС, т.е. преобразование U в Е можно представить в виде следующей схемы
3. Описываем каждое простое явление
Первое явление :
В каждый момент времени напряжение U
уравновешивает падение напряжения на
активной
и
индуктивной
частях
обмотки возбуждения, т.е.
где
L - коэффициент индуктивности обмотки возбуждения / принимается величиной постоянной,
R - активное сопротивление обмотки возбуждения / если температура обмотки не меняется, то эта величина также постоянная / поэтому уравнение первого явления имеет вид :
Для дальнейшего вывода удобнее это
уравнение представить в приращениях
от рабочей точки
,
.
где
Второе явление:
Зависимость магнитного потока от тока возбуждения, кал известно, выражается кривой намагничивания. Если посчитать, что в системе отсутствует гистерезис, то эта зависимость может быть представлена графиком
Очевидно, что зависимость нелинейна, а
поэтому ее следует линеаризовать вблизи
рабочей точки
,
.
Линеаризацию производим методом
касательной, после линеаризации в
приращениях уравнение принимает вид
где
Третье явление:
известно, что ЭДС генератора, пропорциональна магнитному потоку и скорости вращения якоря
где С - постоянная генератора, зависящая
от его конструктивных особенностей.
Если
,
то можем считать, что
тогда
или в приращениях от рабочей точки
,
где
4. Таким образом состояние генератора может быть описано следующей системой уравнений
Решаем эти уравнения относительно
,
или
откуда
и тогда
5. Приводим полученное уравнение к нормальному виду
обозначаем
-
постоянная времени генератора
-
коэффициент передачи генератора /
Окончательно уравнение состояния
генератора в приращениях к рабочей
точке
будет
иметь вид
Связь уравнения состояния с другими характеристиками элемента
Уравнение состояния дает возможность получить все характеристики элемента автоматической системы.
Для получения временных характеристик
необходимо знать изменение входное
величины, т.е.
.
Эта функция времени подставляется в
правую часть уравнения, которое затем
решается относительно выходной величины
У.
Так для получения переходной характеристики
необходимо принять
и
уравнениå после подстановки примет вид
Полученное уравнение представляет собой неоднородное линейное равнение с постоянными коэффициентами. Решение его и есть переходная характеристика.
Доказано, что решение неоднородного уравнения / линейного / равно сумме общего решения соответствующего однородного уравнения и частного решения неоднородного уравнения, т.е.
Y=Yч+Y0
Y- общее решение неоднородного уравнения
Yч - частное решение неоднородного уравнения
Yо- общее решение однородного уравнение
1. Итак, для нахождения решения однородного уравнения для нашего случая записываем однородное уравнение в виде
Заменяя символ производных величиной р в степени, равной порядку производной, а неизвестную функцию У - единицей, получим алгебраическое уравнение, которое называется характеристическим.
Пусть корнями характеристического
уравнения будут
.
Известно, что каждому вещественное
корню
соответствует
составляющая решения
Каждой паре комплексных корней
и
соответствует
составляющая решения, равная
Таким образом, общее решение однородного уравнения имеет вид
2. Частное решение неоднородного уравнения рассмотрим для случая, когда правая часть - постоянная величина •
Известно, что если правая часть обыкновенного линейного дифференциального у равнения с постоянными коэффициентами равна постоянной величине, т.е.
то частным решением неоднородного уравнения может быть также постоянная, т.е.
Yч=D=const
откуда
и
тогда частное решение будет иметь вид
Yч
3. Суммируя общее и частное решения получим уравнение с постоянными коэффициентами
где
-
постоянные интегрирования, определяемые
с помощью начальных условий.
Частотные характеристики могут быть определены, полагая, что входные и выходные величины соответственно равны
;
тогда
Данные выражения подставляем в исходное уравнение и получаем
или
откуда аналитическое выражение будет иметь вид для АФХ
Уничтожая иррациональность в знаменателе и разделяя вещественную
и мнимую части окончательно получим
Пример
Определим характеристики генератора постоянного тока, уравнение состояния которого имеет вид
а. Переходная характеристика
Считаем, что входное воздействие изменилось на единичный скачок
Тогда уравнение переходного процесса будет
характеристическое уравнение
Корень характеристического уравнения
Обще решение уравнения
частное решение
Еч=К
Искомое решение уравнения
примем, что начальные условия нулевые,
т.е. при
тогда
откуда
поэтому
окончательно переходная характеристика имеет выражение
б. Импульсная характеристика
Импульсная характеристика может быть получена дифференцированием переходной , т.е.
тогда
И окончательно аналитическое выражение импульсной характеристики будет иметь вид
в. Амплитудно-фазовая характеристика
Полагаем, что
После подстановки получаем
(так как
)
Откуда аналитическое выражение афх будет иметь вид
Избавляемся от иррациональности в знаменателе
После преобразования получим окончательно
г. Амплитудная частотная характеристика
Аналитическое выражение АЧХ определяется как модуль АФХ, т.е.
окончательно
. Фазовая частотная характеристика.
Аналитическое выражение ФЧХ определяется как аргумент АФХ, т.е.
окончательно
е. Вещественная частотная характеристика.
Аналитическое выражение имеет вид
ж. Мнимая частотная характеристика
з. Логарифмическая амплитудная частотная характеристика определяется выражением
и. Логарифмическая фазовая частотная характеристика.
ЛФХ определяется выражением
