Лекция № 5. Методы описания объектов управления

Как уже было отмечено, решение любой задачи оптимального управления в первую очередь предполагает описание объекта некоторой математической моделью, т.е. математическими соотношениями, которые устанавливают однозначную связь между входными воздействиями и выходными величинами в соответствии со свойствами реального объекта.

В настоящее время при исследовании систем, описываемых обыкновенными дифференциальными уравнениями, наиболее часто используются два способа их представления. Первый их них основан на применении характеристик «вход - выход» системы. В этом случае связь «вход - выход» для линейной системы определяется передаточной и импульсной переходной (весовой) функцией. Пусть дифференциальные уравнения линейного стационарного объекта управления с одной входной U(t) и одной выходной Y(t) переменными имеет вид

(1)

или

(2) ,

которому соответствует передаточная функция

.

Таким образом, передаточная функция системы устанавливает связь между входными и выходными сигналами в области изображений. Импульсная переходная функция есть функция времени, связанная с передаточной функцией соотношением

(3) ,

где - оператор обратного преобразования Лапласа.

Импульсная переходная функция устанавливает связь между входными и выходными сигналами во временной области:

(4)

Передаточная и импульсная переходная функции являются исчерпывающими характеристиками системы лишь в случае определения ее реакции при нулевых начальных условиях.

В последние годы широкое распространение получил другой путь, связанный с описанием поведения системы в абстрактном пространстве состояний (фазовом пространстве). Это объясняется тем, что такое описание во многих случаях оказывается более полным и более удобным. Под состоянием системы понимают минимальную информацию, которая достаточна для того, чтобы предсказать ее будущее поведение. Как известно, чтобы полностью определить решение дифференциального уравнения n - го порядка, в общем случае требуется n начальных условий. В связи с этим при описании системы в пространстве состояний кроме входной u(t)и выходной y(t) координат вводятся в рассмотрение промежуточные переменные (координаты) , характеризующие динамическое поведение исследуемой системы. Например, многомерный объект, состоящий из звеньев , может иметь следующую структуру

Рис. 1

Переменные называют переменными состояния. Их число равно общему порядку системы. Каждая совокупность конкретных числовых значений всех этих переменных полностью определяет состояние системы в данный момент времени и играет роль начальных условий для всего будущего движения системы. Задав числовые значения в момент времени и зная математическое описание системы и входное воздействие u(t) при , можно определить состояние системы в любой момент времени . Следует заметить, что в отличии от входной u и выходной y координат системы, являющихся конкретными физическими величинами, физическая природа координат состояния не является существенной и в их качестве могут выступать некоторые абстрактные переменные, введенные искусственно.

В выборе переменных состояния имеется определенный произвол, поэтому одной и той же передаточной функции могут отвечать бесчисленное множество различных уравнений состояния. Передаточная функция системы по ее описанию в пространстве состояний определяется однозначно. Отсюда следует, что описание системы в пространстве состояний является более общим.

Уравнения в переменных состояния для произвольного, в общем случае нелинейного и нестационарного, объекта имеют вид:

или

(5) ,

где - непрерывные функции.

Управляемая (выходная) координата объекта выражается как функция переменных состояния:

(6)

В случае линейного стационарного объекта уравнения в переменных состояния записываются в виде (скалярная форма):

(7)

(8)

или в векторно-матричной форме:

(9)

(10)

где

; ; ;

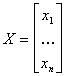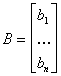d - постоянный коэффициент, если U(t) скаляр.

На рис. 2 приведена структурная схема объекта управления, описываемая с помощью уравнений состояния.

Рис. 2

Найдем связь между передаточной функцией системы и ее уравнениями состояния. Подвергнув (9) и (10) преобразованию Лапласа при нулевых начальных условиях, получим:

(11)

(12)

Из уравнения (11), предполагая существование обратной матрицы, будем иметь:

(13)

Подставляя (13) в (12), найдем

(14)

Отсюда получим передаточную функцию

(15)

Однако, использование описанного метода определения передаточной функции на практике затруднено из-за необходимости обращения матрицы. Передаточную функцию системы невысокого порядка проще найти путем преобразования структурной схемы, составленной на основании уравнений состояния.

Уравнение состояния объекта в нормализованной форме

Уравнения (7-9) неудобны тем, что коэффициенты имеют довольно сложные зависимости от коэффициентов исходного уравнения, описывающего объект управления. Кроме того, при скачкообразных функциях U(t) производные координаты x(t) претерпевают разрыв и изображающая точка будет совершать скачки в фазовом пространстве.

Нормальной формой записи уравнений состояния называют такую форму, когда в качестве переменных состояния используются так называемые нормальные координаты, к которым относятся сама выходная переменная объекта и ее производные до (n-1) - го порядка включительно.

Пусть одномерный объект управления описывается линейным дифференциальным уравнением с постоянными коэффициентами без операторов дифференцирования в правой части.

(16) .

Приняв в качестве переменных состояния , получим уравнения в следующем виде:

(18)

Таким образом, матрицы объекта при записи уравнений состояния в нормальной форме имеют вид

(19) 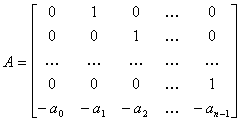; ; 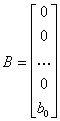d=0

Структурная схема математической модели линейного одномерного объекта управления в форме уравнений состояния (18), показана на рис. 3.

Рис. 3

Каноническая форма уравнения объекта

Канонической называют такую систему уравнений, связь между которыми по переменным отсутствует.

Уравнения состояния в канонической форме могут быть получены различными способами. Один из подходов основан на разложении передаточной функции объекта на элементарные множители.

Другой состоит в том, что переход от уравнения состояния (9) - (10) к канонической форме производится с помощью неособого линейного преобразования линейного пространства в том случае, когда корни характеристического уравнения объекта

(20)

являются различными вещественными числами . Известно, что корни уравнения (20) равны собственным значениям (числам) матрицы A уравнения (9), которые определяются нулями детерминанта ( det ) матрицы .

Собственные значения матрицы A находятся в результате решения алгебраического уравнения , где I - единичная диагональная матрица.

(21) .

Для перехода к канонической форме уравнений объекта производят замену переменных на новые переменные с помощью матрицы Вандермонда G

(22) ,

где матрицы Вандермонда составляется по собственным значениям матрицы A (являются различными вещественными числами).

(23)

и ее det .

Если подставить (17) в уравнение состояния (9), получим

(24)

домножив все члены первого уравнения слева на матрицу, обратную матрице G, получим (при этом ).

(25)

Доказано, что произведение матриц

(26)

Матрица является диагональной матрицей относительно собственных значений матрицы A.

Введем обозначения

(27)

Тогда с учетом (26) и этих обозначений вместо (25) получим векторные уравнения в канонической форме

(28)

для объекта заданного в виде (25). При этом необходимо отметить, что при заданной в (9) матрице C для данного объекта матрица имеет вид единичной строки

(29)

Уравнения (28) можно записать в скалярной форме

(30)

Канонические уравнения объекта в матричной форме для данного случая имеют вид:

(31)

где элементы можно вычислить по формуле

(32)

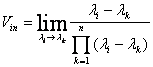
где П - знак произведения.

Структурная схема, соответствующая математической модели объекта управления в канонической форме уравнений (30) имеет вид

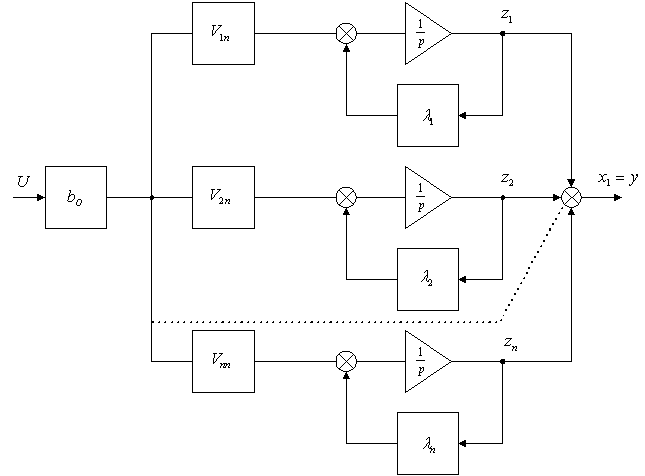
Рис. 4

Переменные в данном случае являются фиктивными координатами, от которых можно перейти к реальным фазовым координатам с помощью линейного преобразования (22).

Удобство канонической формы уравнений (25) состоит в том, что все n уравнений координат являются независимыми и их можно отдельно интегрировать.