6. Умножение линейных операторов.
Пусть
,
,
– линейные пространства над полем
.
Произведением операторов
и
называется отображение
,
действующее из
в
по правилу
для всех
.
(обратите внимание на порядок записи
операторов).
Теорема
8. Если
,
,
то
.
Доказательство.
для любых
.
для любого
и любого числа
.
Поэтому
является линейным отображением.
Задача. Проверьте выполнение следующих свойств умножения операторов:
1.
.
2.
.
3.
.
Теорема
9. При умножении линейных операторов
их матрицы умножаются: если
– базисы в
,
,
,
то
.
Доказательство.
Пусть
,
,
и
,
,
.
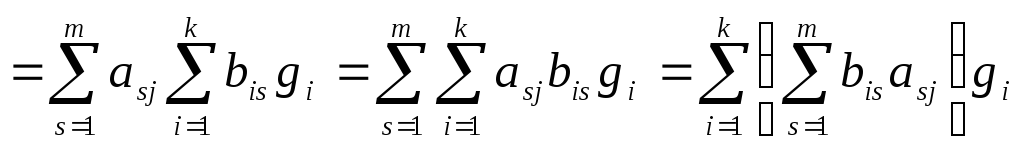– для всех
.
В силу единственности разложения по
базису
получаем
.
7. Невырожденные операторы. Обратный оператор.
Важным классом
линейных операторов, действующих в
пространстве
(т.е. из
в
),
являются невырожденные операторы.
Оператор
называется невырожденным, если
.
Если подпространство
является ненулевым, то оператор
называется вырожденным.
Теорема
10. Невырожденный оператор
осуществляет взаимно однозначное
отображение
на
.
Доказательство.
Для невырожденного оператора
.
Поэтому по теореме 6
,
и
.
Иными словами, каждый элемент
является образом некоторого элемента
при отображении
.
Это значит, что
– сюръективное отображение
на
.
Докажем, что
каждый элемент
имеет только один прообраз при отображении
.
Предположим, что для некоторого
имеются два прообраза:
и
.
Тогда
,
т.е.
.
Но для невырожденного оператора
,
следовательно,
.
Это значит, что
– инъективное отображение.
Пусть
– невырожденный оператор. Тогда для
любого
существует, и притом единственный,
элемент
,
для которого
.
Поэтому определено отображение, ставящее
в соответствие каждому
тот единственный элемент
,
для которого
.
Это отображение называется оператором,
обратным к оператору
;
обозначение:
.
Оператор
действует из
в
по правилу
,
если
.
Очевидно, что
– тождественное отображение.
Теорема
11.
является линейным невырожденным
оператором. В базисе
пространства
его матрица
не вырождена и является обратной к
матрице
.
(Докажите самостоятельно.)
8. Ограниченность линейного оператора в конечномерных нормированных пространствах.
Пусть
и
– конечномерные линейные нормированные
пространства с нормами
и
.
Определение.
Оператор
называется ограниченным, если
существует такое число
,
что для всех
выполнено неравенство
.
Ограниченность оператора
означает, что для всех
,
для которых
,
выполнено неравенство
.
Или, что то же самое, единичный шар
в пространстве
ограниченный оператор переводит во
множество, ограниченное по норме
.
Теорема
12. В конечномерных нормированных
пространствах
и
любой оператор
ограничен.
Доказательство.
Пусть
– базис пространства
.
Разложим произвольный элемент
по этому базису:
.
Пользуясь аксиомами нормы и неравенством
Коши-Буняковского в
,
получаем неравенства
,
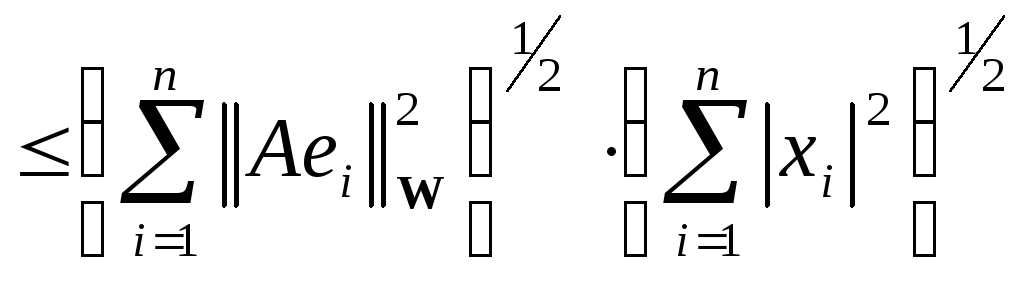
где
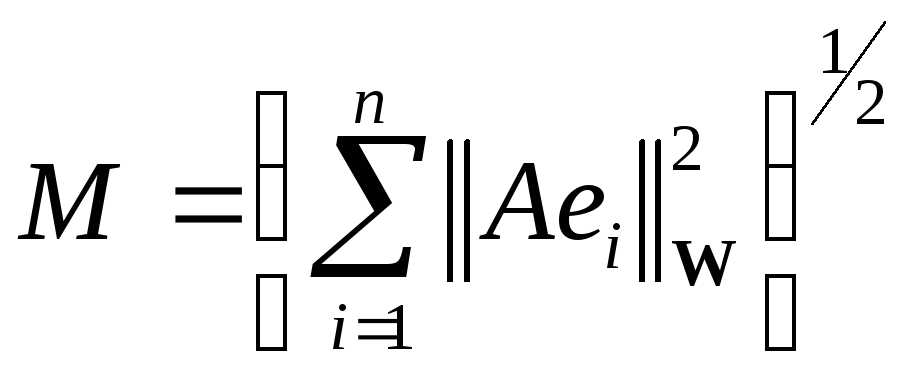
не зависит от
,
а
– евклидова норма в
.
Из эквивалентности норм в конечномерном
пространстве
имеем
для всех
;
.
Отсюда для всех
получаем
,
где
.
Замечание. Для линейных операторов, действующих в бесконечномерных нормированных пространствах, свойство ограниченности может не выполняться.
Из ограниченности
линейного оператора
вытекает, что отображение
:
непрерывно в нуле пространства
:
для любого числа
найдется такое число
,
что из неравенства
следует неравенство
(достаточно выбрать
).
Но в силу линейности оператора
отсюда вытекает, что указанное отображение
непрерывно в каждой точке
.
В самом деле: для любого
найдется
,
при котором из неравенства
следует
.