2. Другие виды уравнений прямой и плоскости.
Уравнения прямой
линии на плоскости
или плоскости в пространстве
можно записать и в другом виде. Пусть
уравнение
прямой
на плоскости
является полным, т.е. все коэффициенты
отличны от нуля. Тогда это уравнение
можно переписать в виде
,
где
,
.
Такое уравнение называется уравнением
прямой в отрезках. Числа
и
равны величинам отрезков, которые прямая
линия отсекает на осях координат (т.е.
длинам отрезков с учетом знака). Совершенно
аналогично уравнение
задает в пространстве
плоскость, которая пересекает все три
оси координат
.
Любой ненулевой
вектор, параллельный прямой линии или
принадлежащий ей, называется её
направляющим вектором. Пусть прямая
на плоскости
проходит через заданную точку
и имеет направляющий вектор
,
лежащий в той же плоскости. Точка
лежит на прямой
тогда и только тогда, когда
и
коллинеарны, т.е. их координаты
пропорциональны:
;
– каноническое уравнение прямой
на плоскости. Если известно, что прямая
проходит через две несовпадающие точки
и
,
то в качестве направляющего вектора
можно взять вектор
.
Тогда получим уравнение прямой
на плоскости в виде
.
В каноническом уравнении прямой линии
знаменатели
могут оказаться равными нулю; тогда
считают, что соответствующий числитель
дроби обращается в нуль. Каноническое
уравнение прямой, проходящей через две
несовпадающие точки, можно записать в
виде
.
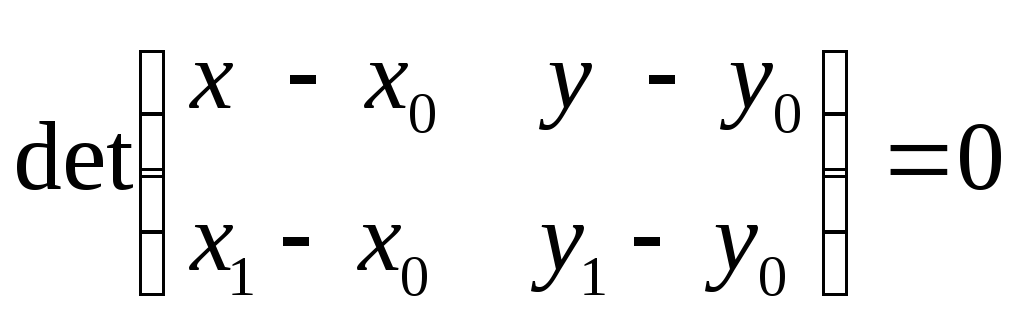Совершенно аналогично можно задать в
пространстве
плоскость. Любой ненулевой вектор,
параллельный плоскости или принадлежащий
ей, называется ее направляющим вектором.
Пусть три различные точки
,
,
не лежат на одной прямой. Тогда векторы
и
не коллинеарны. Точка
будет лежать в одной плоскости с точками
тогда и только тогда, когда векторы
,
и
компланарны, т.е. параллельны некоторой
плоскости или лежат на ней; в этом случае
.
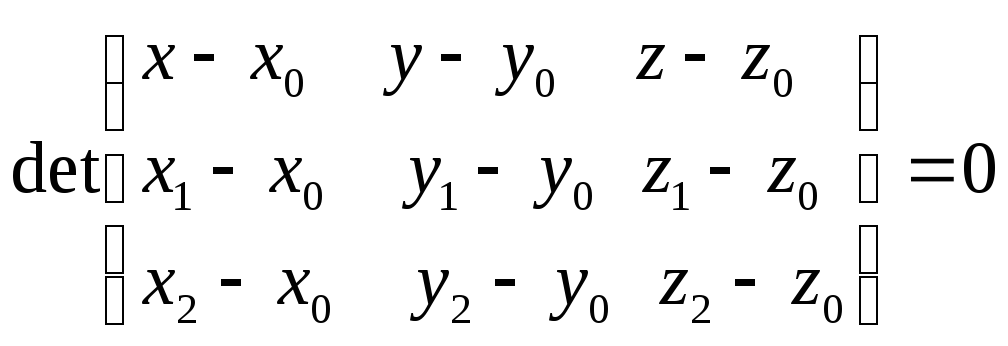Если имеются два направляющих вектора
плоскости
и
,
которые не коллинеарны, то проходящая
через точку
плоскость задается уравнением
;
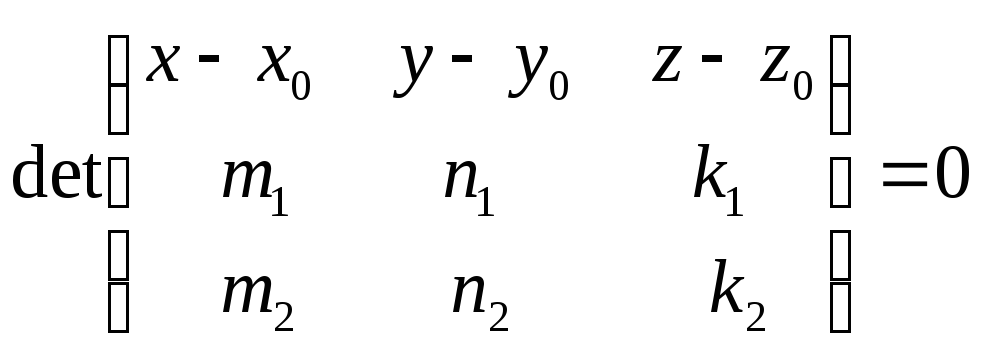– каноническое уравнение плоскости.
Из канонического
уравнения прямой на плоскости
можно получить ее параметрические
уравнения
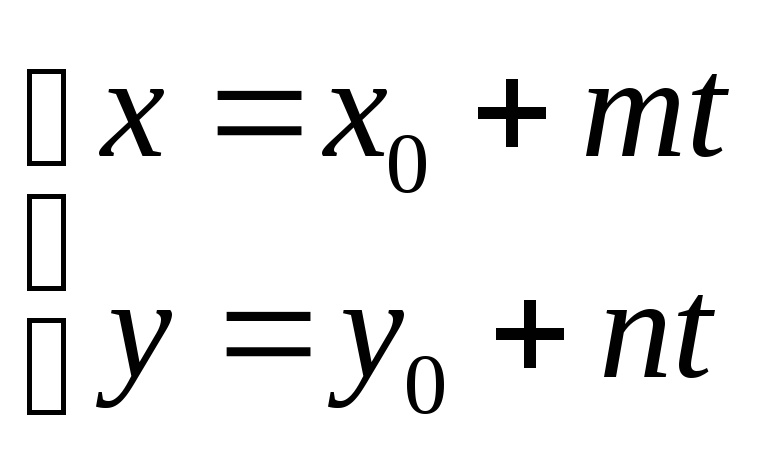, если в качестве параметра
выбрать каждое из указанных равных
отношений. Когда
пробегает все множество действительных
чисел, получаем все точки данной прямой.
Совершенно аналогично можно получить
параметрические уравнения плоскости
,
где
и
– параметры. Если вектор
обозначить через
,
а вектор
–
через
,
то параметрические уравнения плоскости
означают, что
.
Когда
и
независимо пробегают все действительные
значения, получаем все точки плоскости.
3. Уравнения прямой в пространстве.
Прямую, проходящую
через точку
в пространстве
,
можно задать при помощи направляющего
вектора
каноническими уравнениями
или параметрическими уравнениями
.
Если две плоскости в
пересекаются, но не совпадают, то прямую
их пересечения можно задать системой
уравнений
,
в которой каждое уравнение задает
соответствующую плоскость. За направляющий
вектор этой прямой можно принять
векторное произведение
нормальных векторов плоскостей:
,
(см. следующее замечание о векторном
произведении).
Замечание.
Пусть
,
,
– упорядоченная тройка некомпланарных
направленных отрезков. Она называется
правой тройкой, если
,
,
расположены так, как большой палец
правой руки, ее несогнутый указательный
палец и средний палец соответственно.
( Если
,
,
расположены как те же пальцы левой
руки, то тройка называется левой.) Введем
операцию, которая неколлинеарным
направленным отрезкам
,
ставит в соответствие направленный
отрезок
по следующим правилам:
и
;
тройка
,
,
– правая; длина
равна площади параллелограмма,
образованного
и
.
Такая операция называется векторным
произведением:
.
В евклидовом
пространстве
прямой линией является любая одномерная
плоскость. Пусть
– вектор сдвига, а
– ненулевой вектор одномерного
направляющего подпространства. Тогда
параметрическое векторное уравнение
задает прямую линию, проходящую через
и имеющую направляющий вектор
.
Если точки
и
различны, то единственная прямая,
проходящая через
и
,
определяется уравнением
.
Прямую в
можно задать и как множество точек
пересечения
гиперплоскостей: если
– векторы, ортогональные к направляющим
подпространствам
,
то система уравнений
задает пересечение
гиперплоскостей. Если это пересечение
не пусто, т.е. система имеет хотя бы одно
решение
,
то указанное пересечение является
плоскостью, которую можно задать системой
уравнений
,
где вектор
является произвольным вектором из
.
Если векторы
линейно независимы, то размерность
указанного пересечения равна 1, т.е.
исходная система определяет прямую в
(см.
тему 3).