3. Матрица линейного оператора.
Пусть
и
– базисы конечномерных пространств
и
соответственно. Линейный оператор
однозначно определяется заданием
векторов
.
В свою очередь
,
,
однозначно определяются своими
координатами в базисе
:
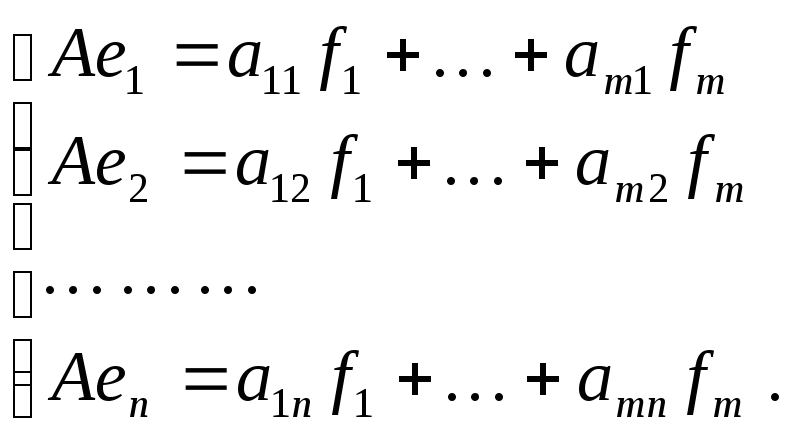
(Обратите внимание на выбранный
порядок индексов коэффициентов этого
разложения.)
-матрица
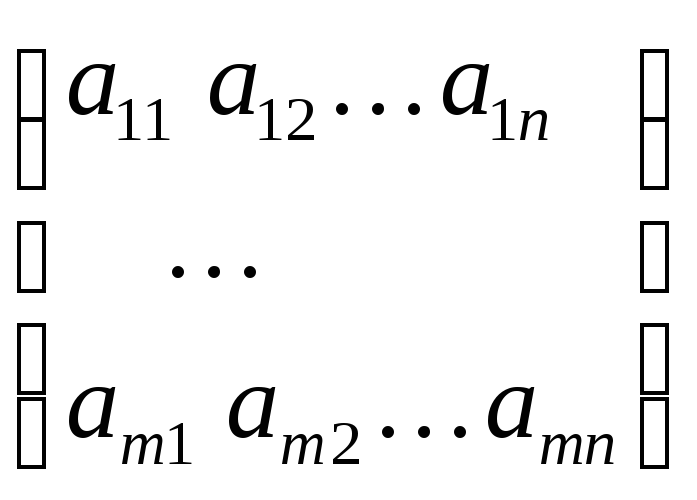называется матрицей оператора
в паре базисов
и
.
Из единственности разложения вектора
по базису следует, что при фиксированных
и
матрица линейного оператора определена
однозначно. Ее
–ый
столбец состоит из координат вектора
в базисе
.
Теорема
2. Пусть
,
.
Между множеством
всех линейных операторов, действующих
из
в
,
и множеством
всех
-матриц
можно установить взаимно однозначное
соответствие.
Доказательство.
Для построения указанного соответствия
достаточно фиксировать базисы
и
пространств
и
.
Каждому оператору
поставим в соответствие его матрицу
в паре базисов
и
.
Матрица
выбором оператора
определена однозначно. Докажем
биективность построенного отображения
операторов на матрицы. Это отображение
сюръективно, так как любую матрицу
можно рассматривать как матрицу линейного
оператора, действующего из
в
и переводящего базисные векторы
в векторы
,
.
Это отображение инъективно, так как
различные операторы
и
,
действующие из
в
,
не совпадают полностью на векторах
базиса
, а значит имеют разные матрицы
и
.
Если в линейном
пространстве
выбран базис
,
то координаты
элемента
в этом базисе будем записывать в виде
вектора-столбца. Точно так же
координаты
элемента
в базисе
будем записывать в виде вектора-столбца.
Теорема
3. Пусть
и
– матрица этого оператора в паре базисов
и
.
Если
, то
.
Доказательство.
Пусть
,
,
.
Утверждение
равносильно соотношениям
,
.
Докажем их:
.
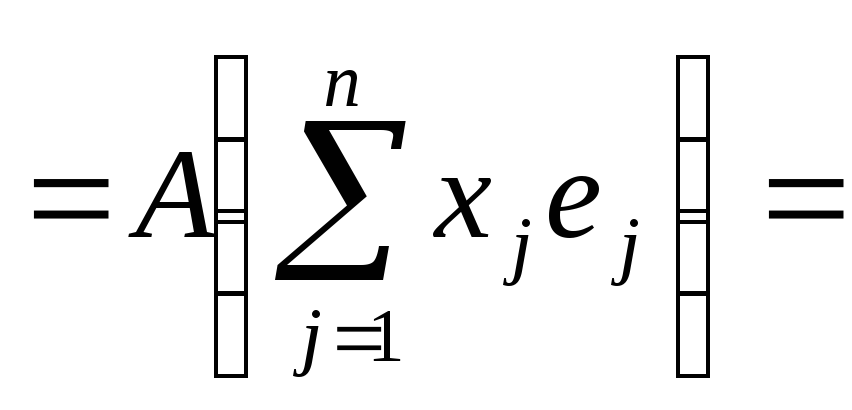
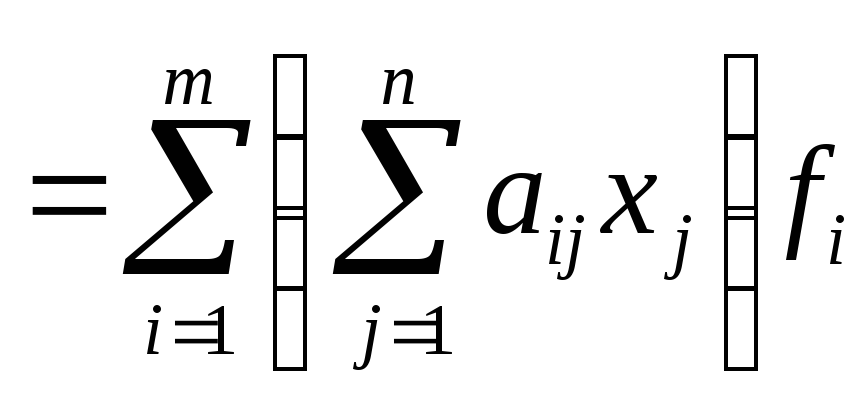Напомним, что
если в одном и том же линейном пространстве
выделены два базиса, то они связаны
невырожденной матрицей перехода (см.
тему 2). Как и ранее, элементы базисов
будем перечислять в строке:
,
.
Пусть
и
– два базиса пространства
с матрицей перехода
,
и
– два базиса пространства
с матрицей перехода
.
Одному и тому же линейному оператору
,
действующему из
в
,
в паре базисов
и
соответствует матрица
,
а в паре базисов
и
– матрица
.
Теорема
4. Матрицы
и
линейного оператора
,
действующего из
в
,
в различных парах базисов связаны
соотношением
.
Доказательство.
Для любого
и
имеем
,
,
,
;
,
,
=
,
.
Определение.
Две прямоугольные матрицы
и
одинаковых размеров называются
эквивалентными, если существуют
такие невырожденные квадратные матрицы
и
,
что
.
Следствие 1. Матрицы линейного оператора в различных парах базисов эквивалентны.
Следствие 2. Ранг матрицы линейного оператора не зависит от выбора базисов.
Поскольку для
любых пар базисов
и
,
это число характеризует сам оператор
;
будем обозначать его
.
Теорема
5. Матрицы
эквивалентны тогда и только тогда, когда
они являются матрицами одного и того
же линейного оператора, действующего
из
в
,
где
,
.
Доказательство.
Необходимость.
Пусть матрицы
и
эквивалентны:
и
,
где
и
– невырожденные матрицы. Рассмотрим
произвольные линейные пространства
и
над полем
размерностей
,
.
Выберем в
базис
,
а в
– базис
.
В силу взаимно однозначного соответствия
множеств
и
существует единственный оператор,
который в паре базисов
имеет матрицу
.
Невырожденные матрицы
и
могут служить матрицами перехода к
другим базисам в
и
:
,
.
Тогда тот же линейный оператор в паре
базисов
имеет матрицу
.
Достаточность была доказана в теореме 4.
Если
и оператор
,
то образ и прообраз при отображении
естественно рассматривать в одном и
том же базисе пространства
.
В базисе
этот оператор определяется квадратной
матрицей
.
В другом базисе
пространства
оператор
определяется квадратной матрицей
.
Тогда по доказанному выше
,
где
,
.
Отсюда
.
Определение.
Две квадратные матрицы
и
одинаковых размеров называются подобными,
если существует такая невырожденная
матрица
,
что
.
Из теоремы 5 следует, что две
квадратные матрицы одинаковых размеров
подобны тогда и только тогда, когда они
являются матрицами одного и того же
оператора
.
Важной числовой
характеристикой квадратной матрицы
является ее след
,
равный сумме диагональных элементов:
.
Утверждение.
Если матрицы
и
подобны, то
и
.
(Докажите самостоятельно.)