
- •Тема 5. Уравнения прямой и плоскости.
- •1. Общее уравнение прямой. Общее уравнение плоскости.
- •2. Другие виды уравнений прямой и плоскости.
- •3. Уравнения прямой в пространстве.
- •4. Основные задачи на прямую и плоскость в .
- •5. Взаимное расположение прямой и плоскости. Взаимное расположение плоскостей в линейном пространстве.
- •Тема 6. Линейные операторы.
- •1. Взаимно однозначные отображения.
- •2. Линейные операторы.
- •3. Матрица линейного оператора.
- •4. Ядро и образ линейного оператора.
- •5. Линейное пространство операторов.
- •6. Умножение линейных операторов.
- •7. Невырожденные операторы. Обратный оператор.
- •8. Ограниченность линейного оператора в конечномерных нормированных пространствах.
- •9. Норма линейного оператора.
Тема 6. Линейные операторы.
1. Взаимно однозначные отображения.
Перенесем
некоторые понятия, известные из
элементарной теории функций, на
произвольные отображения одного
множества в другое. Пусть
![]() и
и
![]() – два произвольных множества, а
– два произвольных множества, а
![]() – отображение, действующее из
– отображение, действующее из
![]() в
в
![]() ;
;
![]() .
Задание отображения
.
Задание отображения
![]() подразумевает, что во множестве
подразумевает, что во множестве
![]() имеется некоторое подмножество
имеется некоторое подмножество
![]() , на элементах которого определено
отображение
, на элементах которого определено
отображение
![]() (
(![]() – область определения
– область определения
![]() ),
а во множестве
),
а во множестве
![]() имеется подмножество
имеется подмножество
![]() (оно называется областью значений или
образом отображения
(оно называется областью значений или
образом отображения
![]() ),
причем каждому элементу
),
причем каждому элементу
![]()
![]() ставится в соответствие единственный
элемент
ставится в соответствие единственный
элемент
![]()
![]() :
:
![]() .
Отображение
.
Отображение
![]() называется инъективным, если для любых
двух элементов
называется инъективным, если для любых
двух элементов
![]()
![]() из условия
из условия
![]() следует
следует
![]() .
Отображение
.
Отображение
![]() называется сюръективным, если
называется сюръективным, если
![]()
![]() .
Сюръективность отображения
.
Сюръективность отображения
![]() означает, что для любого элемента
означает, что для любого элемента
![]()
![]() уравнение
уравнение
![]() имеет решение
имеет решение
![]() (возможно, не единственное). Отображение
(возможно, не единственное). Отображение
![]() называется взаимно однозначным или
биективным, если оно инъективно и
сюръективно.
называется взаимно однозначным или
биективным, если оно инъективно и
сюръективно.
Если
![]()
![]() ,
то тот единственный элемент
,
то тот единственный элемент
![]()
![]() ,
для которого
,
для которого
![]() ,
называется образом элемента
,
называется образом элемента
![]() при отображении
при отображении
![]() .
.
Если
![]()
![]() ,
то всякий элемент
,
то всякий элемент
![]()
![]() ,
для которого
,
для которого
![]() ,
называется прообразом элемента
,
называется прообразом элемента
![]() при отображении
при отображении
![]() .
Элемент
.
Элемент
![]() может иметь более одного прообраза; но
если отображение
может иметь более одного прообраза; но
если отображение
![]() инъективно, то у каждого элемента
инъективно, то у каждого элемента
![]()
![]() имеется только один прообраз.
имеется только один прообраз.
Задача.
![]() ,
,
![]() ,
,

Найдите
![]() и
и
![]() .
Найдите все прообразы числа
.
Найдите все прообразы числа
![]() .
.
Найдите образ
числа
![]() .
.
Задача.
![]() ,
,
![]() ,
,
![]() .
Найдите
.
Найдите
![]() и
и
![]() .
.
![]() Найдите
образ числа
Найдите
образ числа
![]() .
Найдите все прообразы числа
.
Найдите все прообразы числа
![]() .
Найдите подмножества
.
Найдите подмножества
![]() ,
на которых
,
на которых
![]() биективно.
биективно.
2. Линейные операторы.
Пусть![]() и
и
![]() – конечномерные линейные пространства
над общим полем чисел
– конечномерные линейные пространства
над общим полем чисел
![]() (
(![]() или
или
![]() ).
Отображение
).
Отображение
![]() :
:![]() называется линейным отображением
пространства
называется линейным отображением
пространства
![]() в пространство
в пространство
![]() ,
если для любых
,
если для любых
![]()
![]() и любого числа
и любого числа
![]()
![]() выполняются равенства
выполняются равенства
![]() .
.
![]()
![]() ,
,
![]()
![]() .
Линейное отображение называется также
линейным оператором, действующим из
пространства
.
Линейное отображение называется также
линейным оператором, действующим из
пространства
![]() в пространство
в пространство
![]() ;
обозначение:
;
обозначение:
![]()
![]()
![]() .
Операторы
.
Операторы
![]() и
и
![]() ,
действующие из
,
действующие из
![]() в
в
![]() ,
называются равными, если
,
называются равными, если
![]() для любого
для любого
![]()
![]() .
.
Примеры линейных операторов.
-
Отображение
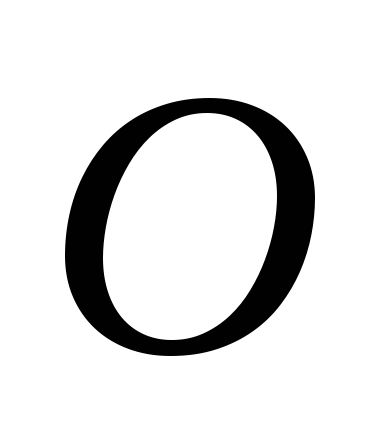 :
:
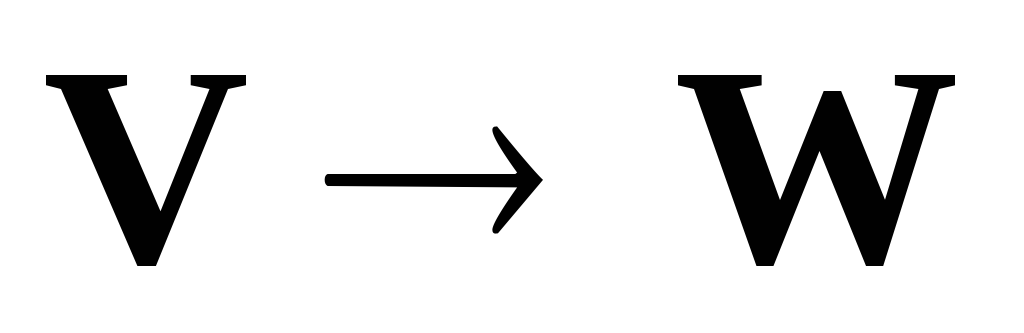 ,
которое каждый вектор
,
которое каждый вектор
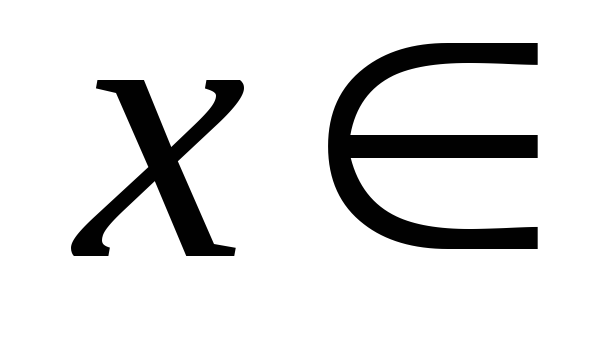
 переводит в нулевой вектор
переводит в нулевой вектор

 ,
является линейным и называется нулевым
оператором.
,
является линейным и называется нулевым
оператором. -
Отображение
 :
:
 ,
которое каждый вектор
,
которое каждый вектор
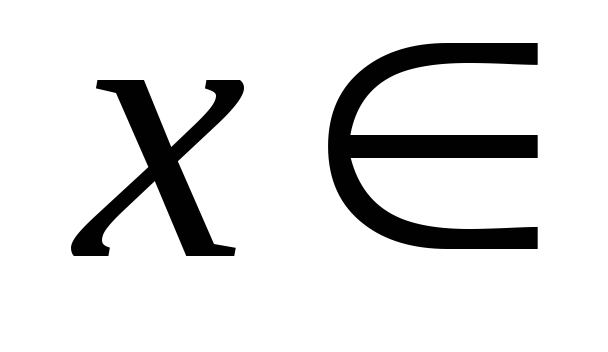
 переводит в
переводит в
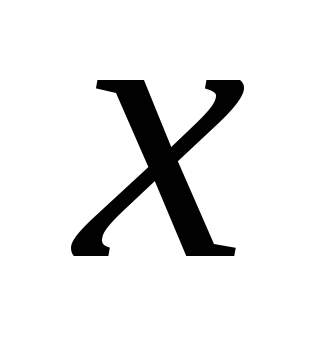 ,
является линейным и называется
тождественным оператором.
,
является линейным и называется
тождественным оператором. -
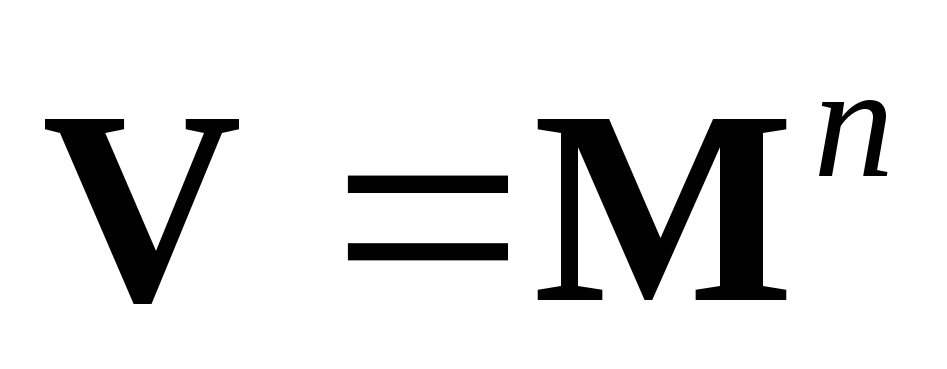 – линейное пространство многочленов
степени не выше
– линейное пространство многочленов
степени не выше
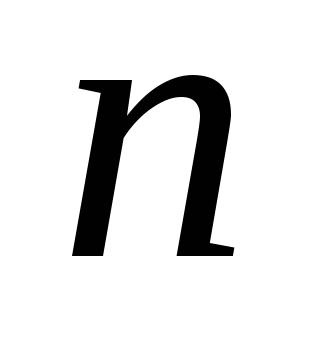 ,
,
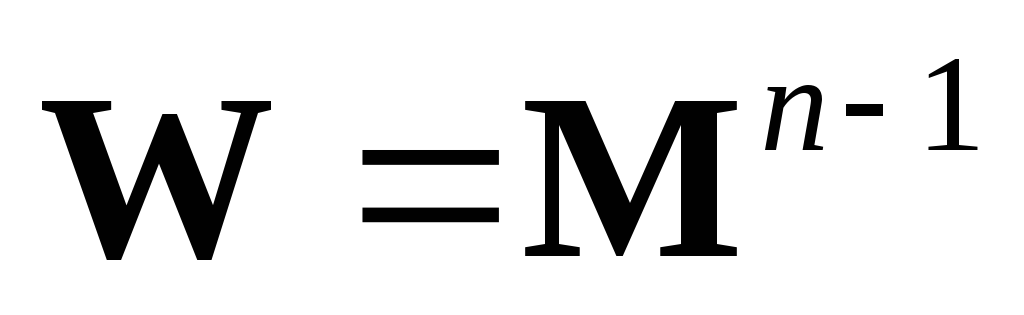 .
.
 – оператор дифференцирования:
– оператор дифференцирования:
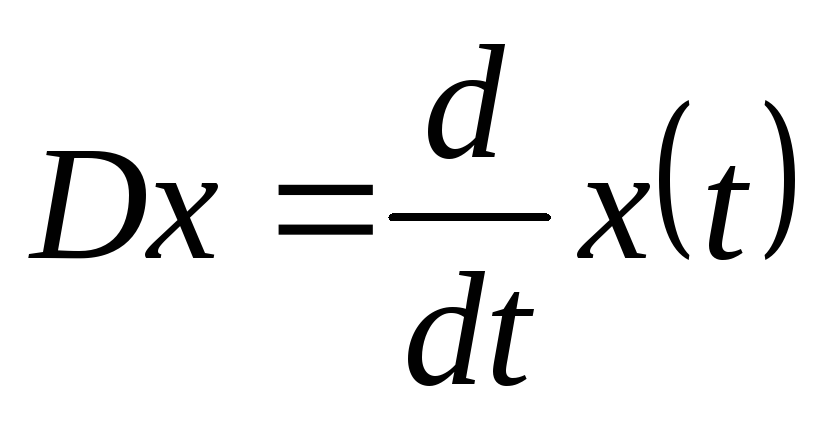 ,
,

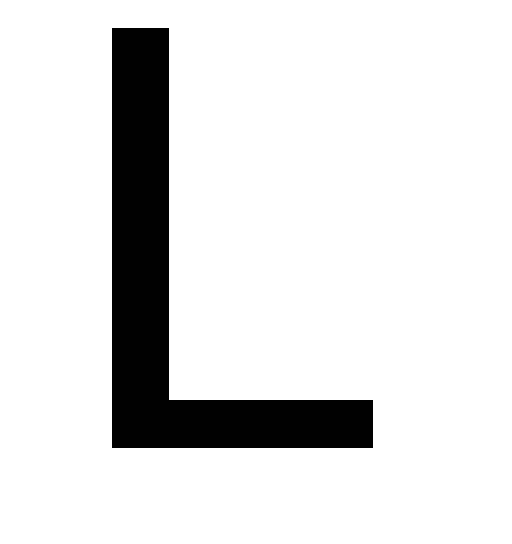
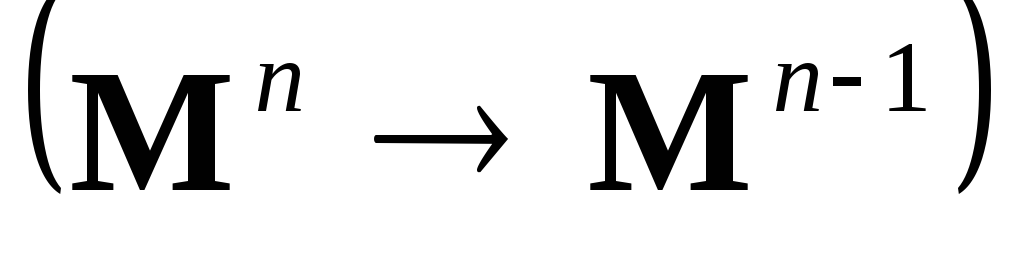 .
. -
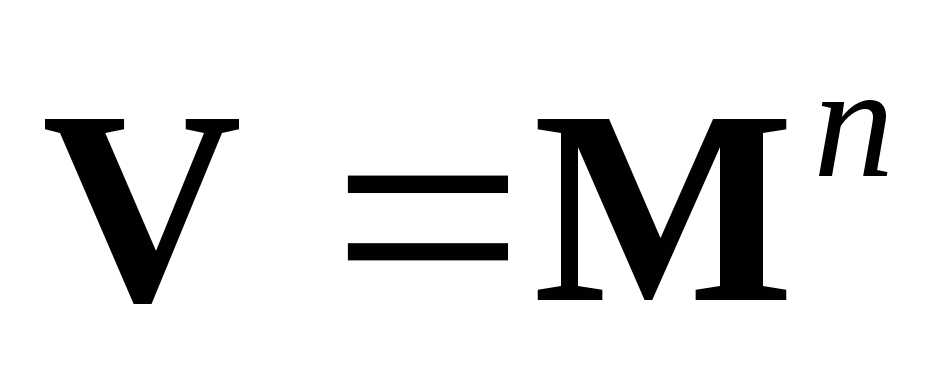 ,
,
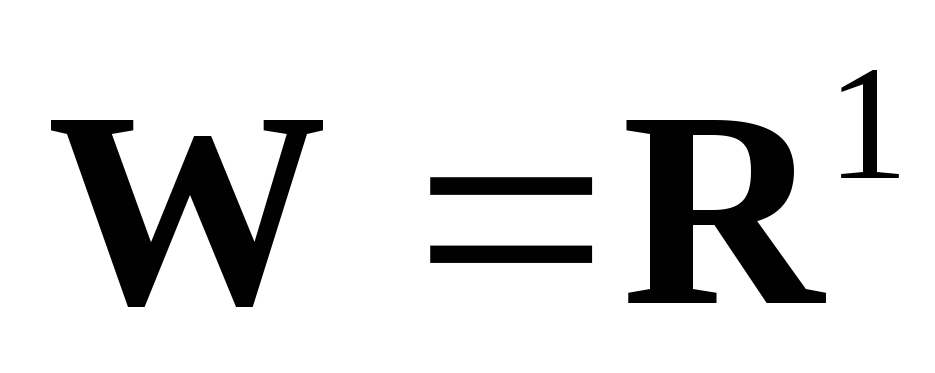 .
.
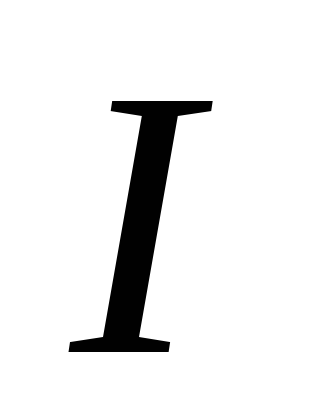 – оператор интегрирования на фиксированном
отрезке
– оператор интегрирования на фиксированном
отрезке
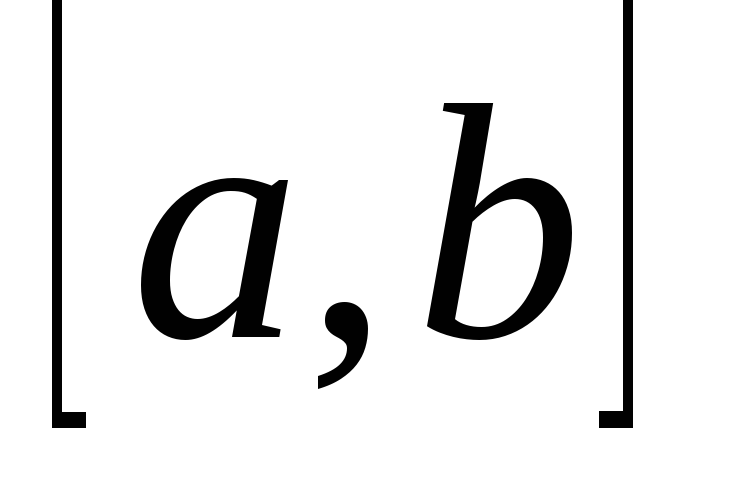 :
:
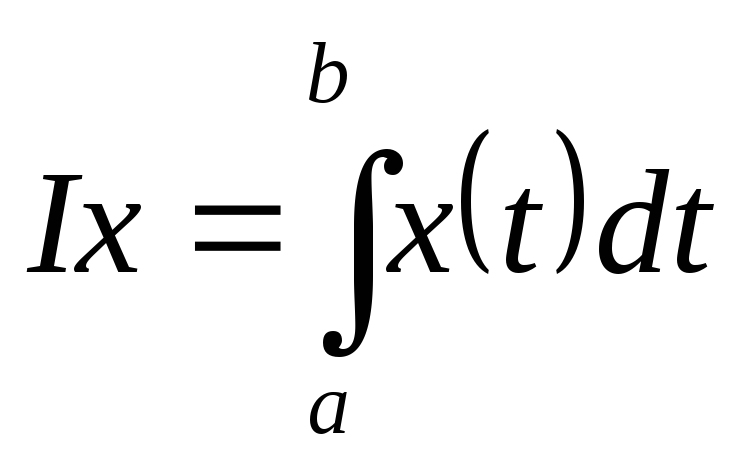 .
.
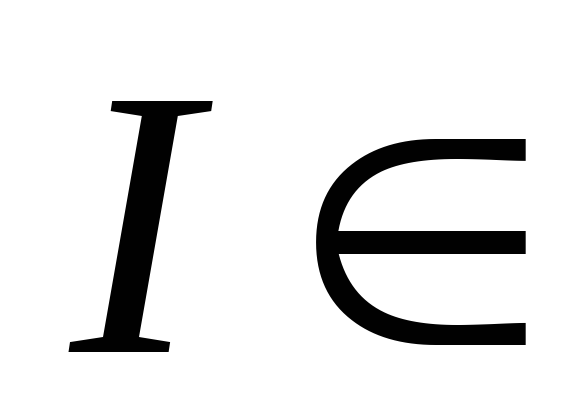

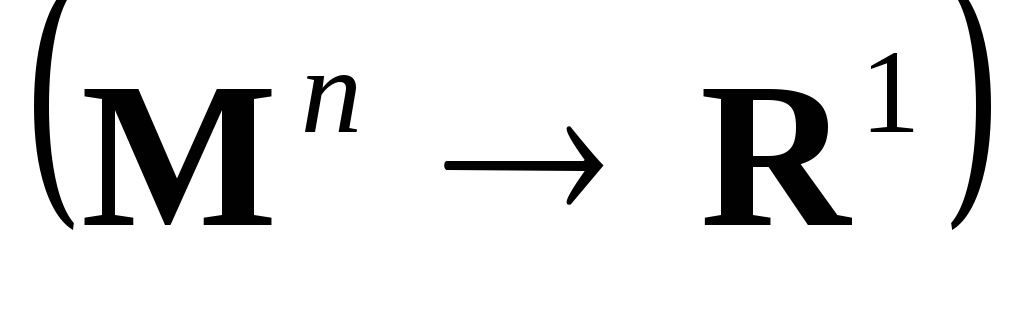 .
. -
 . Отождествим
. Отождествим
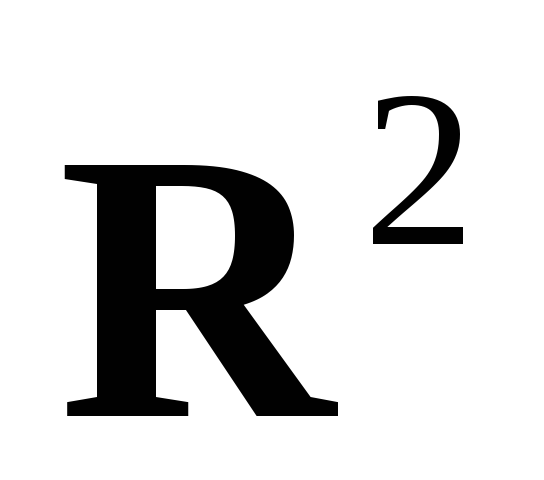 с плоскостью и зададим оператор
геометрически. Оператор
с плоскостью и зададим оператор
геометрически. Оператор
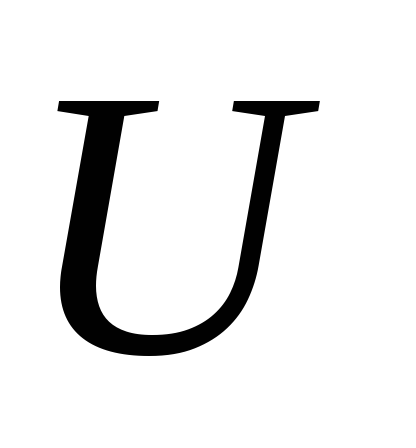 поворачивает каждый направленный
отрезок
поворачивает каждый направленный
отрезок
 (с началом в начале координат) на угол
(с началом в начале координат) на угол
 против часовой стрелки вокруг начала
координат.
против часовой стрелки вокруг начала
координат.
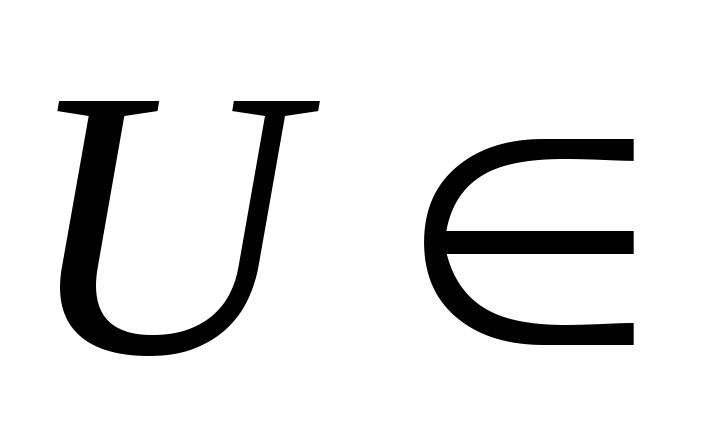
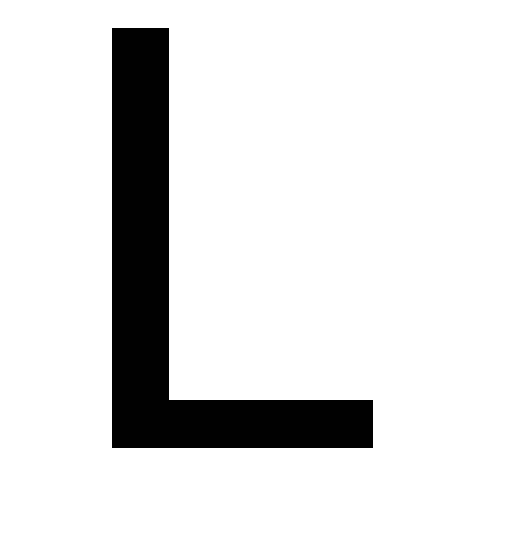
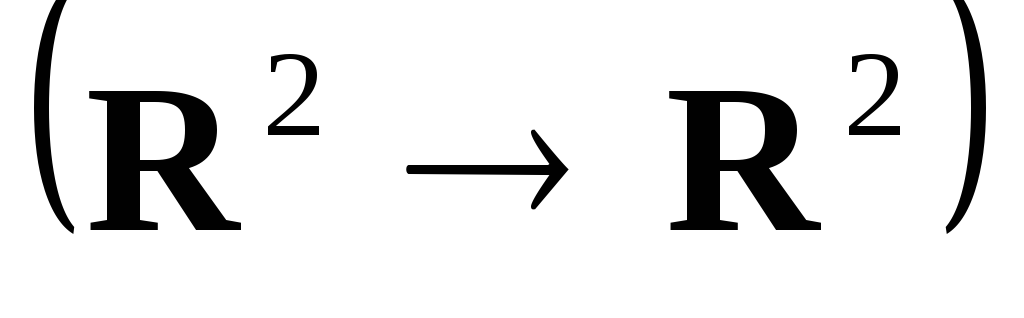 .
.
Из определения линейного оператора вытекают его простейшие свойства:
-
Линейный оператор переводит
 в
в
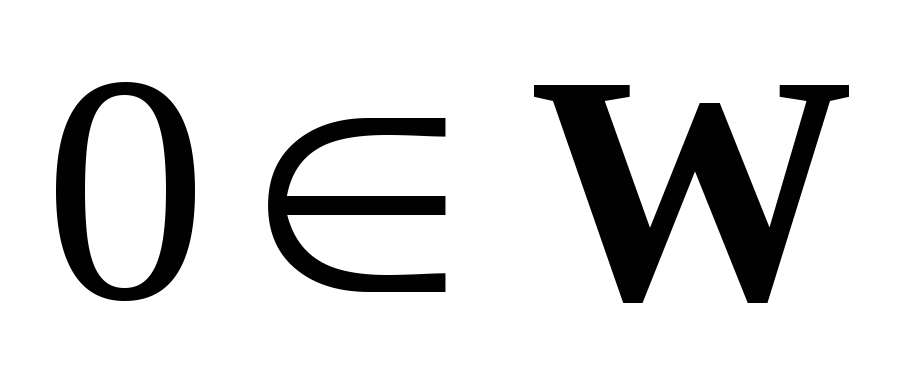 .
. -
Линейный оператор сохраняет линейную комбинацию:

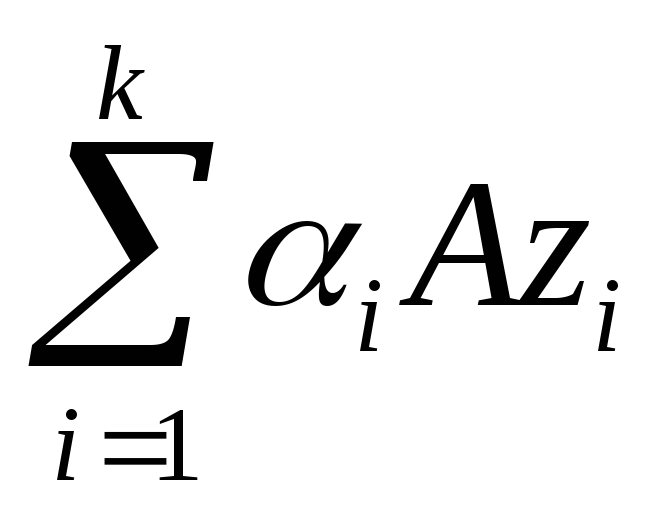 ,
,
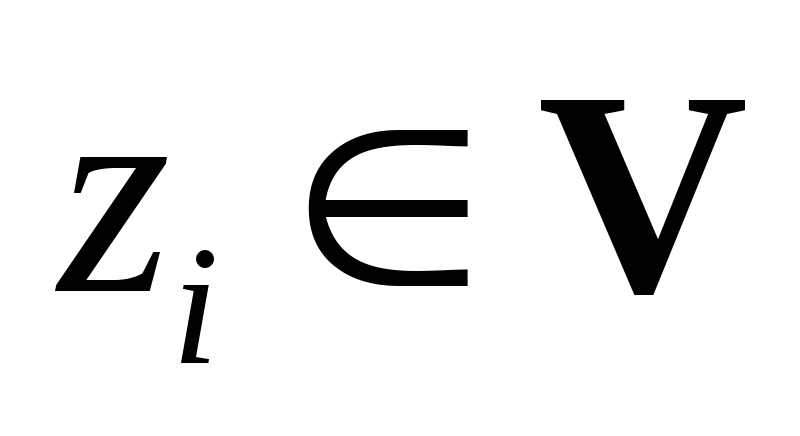 .
. -
Линейный оператор всякую линейно зависимую систему элементов переводит в линейно зависимую.
Замечание. Линейный оператор может не сохранять линейную независимость системы элементов. Приведите пример!
Задать линейный
оператор
![]()
![]() можно,
описав его действие на каждый элемент
пространства
можно,
описав его действие на каждый элемент
пространства
![]() .
Но достаточно это сделать только для
векторов
.
Но достаточно это сделать только для
векторов
![]() некоторого базиса пространства
некоторого базиса пространства
![]() .
Зная все
.
Зная все
![]() ,
,
![]() ,
можно найти образ любого вектора
,
можно найти образ любого вектора
![]() :
:
![]()
![]() (здесь
(здесь
![]() – координаты
– координаты
![]() в базисе
в базисе
![]() ).
).
Теорема
1. Пусть
![]() – базис пространства
– базис пространства
![]() ,
а
,
а
![]() – произвольные векторы пространства
– произвольные векторы пространства
![]() .
Тогда существует, и притом единственный,
линейный оператор
.
Тогда существует, и притом единственный,
линейный оператор
![]()
![]() ,
который переводит векторы
,
который переводит векторы
![]() в векторы
в векторы
![]() соответственно.
соответственно.
Доказательство.
Зададим действие искомого оператора
сначала только на векторы
![]() :
:
![]()
![]() ,
,
![]() .
Распространим его действие на все
векторы
.
Распространим его действие на все
векторы
![]() :
если
:
если
![]() ,
то положим
,
то положим
![]()
![]()
![]() .
Из единственности разложения
.
Из единственности разложения
![]() по базису
по базису
![]() следует, что такое правило однозначно
определяет образ любого вектора.
Линейность построенного оператора
вытекает из линейности координат
векторов пространства
следует, что такое правило однозначно
определяет образ любого вектора.
Линейность построенного оператора
вытекает из линейности координат
векторов пространства
![]() в фиксированном базисе. Если бы существовал
другой оператор
в фиксированном базисе. Если бы существовал
другой оператор
![]() ,
удовлетворяющий условиям теоремы, то
для любого
,
удовлетворяющий условиям теоремы, то
для любого
![]() мы имели бы
мы имели бы
![]()
![]()
![]() ,
т.е.
,
т.е.
![]() .
.
Следствие.
Линейные операторы
![]() и
и
![]() ,
действующие из
,
действующие из
![]() в
в
![]() ,
равны тогда и только тогда, когда они
совпадают на векторах базиса
,
равны тогда и только тогда, когда они
совпадают на векторах базиса
![]() .
.
