4. Основные задачи на прямую и плоскость в .
Задача
1. Найти уравнение прямой, проходящей
через данную точку
и перпендикулярной данной плоскости
.
Ответ:
.
Задача
2. Найти уравнение плоскости,
проходящей через данную точку
и перпендикулярной данной прямой
.
Ответ:
.
Задача
3. Найти уравнение плоскости,
проходящей через данную прямую
и через данную точку
, не лежащую на этой прямой.
Ответ:
.
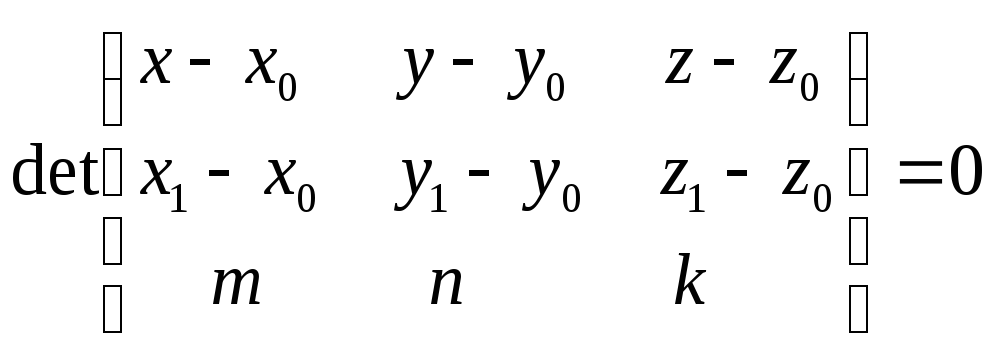Задача
4. Найти уравнение плоскости,
проходящей через данную прямую
и параллельной другой данной прямой
(две данные прямые не параллельны).
Ответ:
.
Задача
5. Найти уравнение плоскости,
проходящей через данную точку
и параллельной двум данным прямым
,
(две данные прямые не параллельны).
Ответ:
.
Задача
6. Найти уравнение плоскости,
проходящей через данную прямую
и перпендикулярной данной плоскости
(данная прямая и данная плоскость не
перпендикулярны).
Ответ:
.
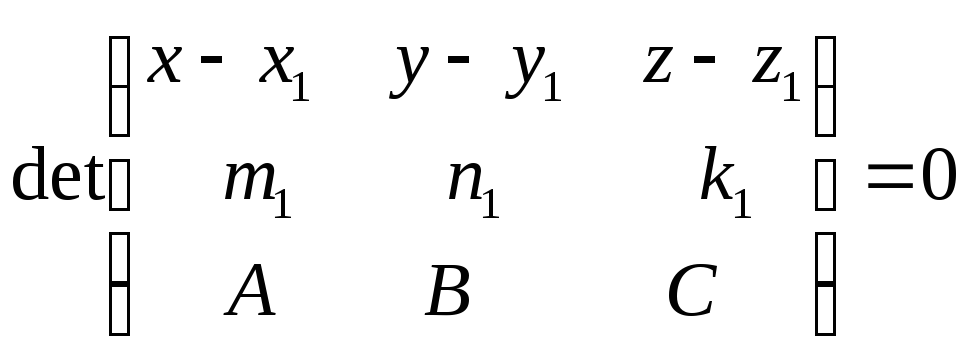Задача
7. Найти уравнение плоскости,
проходящей через две данные точки
и
и перпендикулярной данной плоскости
(прямая
и данная плоскость не перпендикулярны).
Ответ:
.
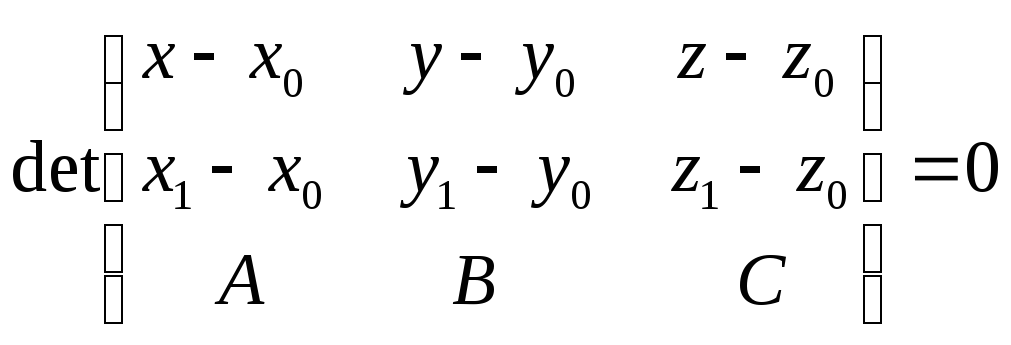5. Взаимное расположение прямой и плоскости. Взаимное расположение плоскостей в линейном пространстве.
Теорема
3. Пусть плоскость
задана в
общим уравнением
,
а прямая
задана каноническими уравнениями
.
Прямая
принадлежит плоскости
тогда и только тогда, когда
и
.
Прямая
параллельна плоскости
тогда и только тогда, когда
и
.
Прямая
перпендикулярна плоскости
тогда и только тогда, когда
.Угол
между прямой
и плоскостью
определяется из уравнения
,
.
(Докажите самостоятельно.)
Напомним, что
на плоскости
возможны только три случая взаимного
расположения двух прямых линий: обе
прямые совпадают, пересекаются в одной
точке, параллельны. В пространстве
возможны следующие случаи взаимного
расположения двух прямых: обе прямые
совпадают, пересекаются в одной точке,
параллельны, скрещиваются. Прямая и
плоскость в
могут пересекаться целиком по этой
прямой, пересекаться в одной точке, быть
параллельными. Две плоскости в
либо совпадают, либо пересекаются по
прямой линии, либо параллельны.
Рассмотрим
теперь две плоскости
и
в линейном пространстве
. Пусть
и
– их направляющие подпространства,
,
.
Пересечение
является подпространством в
,
размерность которого удовлетворяет
неравенствам
(правое неравенство очевидно,
а левое неравенство следует из того,
что
– см. тему 2).
Предположим
сначала ,что
и
имеют хотя бы одну общую точку:
( означает пустое
множество). Если
,
т.е.
,
то
и
пересекаются в единственной точке. Если
,
то
и
пересекаются по прямой линии. Вообще,
в рассматриваемом случае
и
пересекаются по некоторой плоскости
размерности
.
В частности, если, например,
, то пересечением
и
является вся плоскость
.
Если
,
то и
.
Теперь рассмотрим
случай, когда
и
не имеют общих точек:
.
Если одно из направляющих подпространств
этих плоскостей принадлежит другому
направляющему подпространству, то
и
параллельны. Если ни одно из этих
направляющих подпространств не
принадлежит целиком другому направляющему
подпространству, то
и
скрещиваются.
Для выяснения
взаимного расположения
и
зададим обе плоскости параметрическими
уравнениями. Пусть
– линейно независимые направляющие
векторы плоскости
;
они образуют базис ее направляющего
подпространства:
.
Пусть
– вектор сдвига подпространства
.Тогда
все точки плоскости
имеют вид
,
где
– независимо изменяющиеся параметры.
Пусть
– линейно независимые направляющие
векторы плоскости
;
.
Пусть
– вектор сдвига подпространства
.
Все точки плоскости
имеют вид
,
где
– независимо изменяющиеся параметры.
Вопрос о существовании общих точек у
плоскостей
и
сведен к вопросу о совместности системы
линейных алгебраических уравнений
относительно неизвестных
,
.
Ответ на него дается теоремой
Кронекера-Капелли (см. тему 3). Для
нахождения
надо найти число линейно независимых
решений однородной системы уравнений
относительно тех же
неизвестных (см. тему 3).