1. (Проекция суммы равна сумме проекций);

2. (Проекция произведения вектора на число равна произведению проекции вектора на число).

Базис называется ортогональным, если его векторы попарно ортогональны.

Ортогональный базис называется ортонормированным, если его векторы по длине равны единице. Для ортонормированного базиса в пространстве часто используют обозначения .

Теорема: В ортонормированном базисе координаты векторов есть соответствующие ортогональные проекции этого вектора на направления координатных векторов.

Пример: Пусть вектор единичной длины образует с вектором ортонормированного базиса на плоскости угол φ (рис.10), тогда .

Пример: Пусть вектор единичной длины образует с векторами , и ортонормированного базиса в пространстве углы α, β, γ, соответственно (рис.11), тогда . Причем . Величины cosα, cosβ, cosγ называются направляющими косинусами вектора

Глава 4. Понятие базиса. Свойства вектора в данном базисе

Определение: Базисом в пространстве называется любая упорядоченная тройка некомпланарных векторов.

Определение: Базисом на плоскости называется любая упорядоченная пара неколлинеарных векторов.

Базис в пространстве позволяет однозначно сопоставить каждому вектору упорядоченную тройку чисел – коэффициенты представления этого вектора в виде линейной комбинации векторов базиса. Наоборот, каждой упорядоченной тройке чисел при помощи базиса мы сопоставим вектор , если составим линейную комбинацию .

Числа – называются компонентами (или координатами) вектора в данном базисе (записывается ).

Теорема: При сложении двух векторов их координаты складываются. При умножении вектора на число все координаты вектора умножаются на это число.

Определение и свойства координат вектора на плоскости аналогичны. Вы легко можете сформулировать их самостоятельно.

2.1 Непрерывность функции

Определение 1. Функция f(x) называется непрерывной в точке x₀, если .

Более подробно это расшифровывается следующим образом:

1. .

2. . Другими словами, непрерывная функция характеризуется тем свойством, что можно менять местами знак функции и знак предела.

3. Обозначим (приращение аргумента) и (приращение функции). Тогда непрерывная функция характеризуется тем свойством, что при также и , то есть бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции.

Определение 2. Функция f(x) называется непрерывной на множестве Х, если она непрерывна в каждой точке этого множества.

2.2                 Разрывы функции

Определение. Точки, где функция f(x) не является непрерывной, называются точками разрыва функции f(x).

Для классификации точек разрыва рассмотрим предел слева и предел справа функции f(x). Тогда имеет место следующая классификация точек разрыва.

1. Устранимый разрыв.

Он имеет место, когда выполнено условие

.

В данном случае достаточно изменить значение функции в точке x₀, чтобы разрыва не стало.

Рис. 2.1 Вид устранимого разрыва

2. Разрыв первого рода (скачок).

Разрыв первого рода (скачок) получается тогда, когда односторонние пределы и существуют, конечны, но не равны между собой, то есть .

Вид функции в случае разрыва первого рода приведен на рис. 2.2.

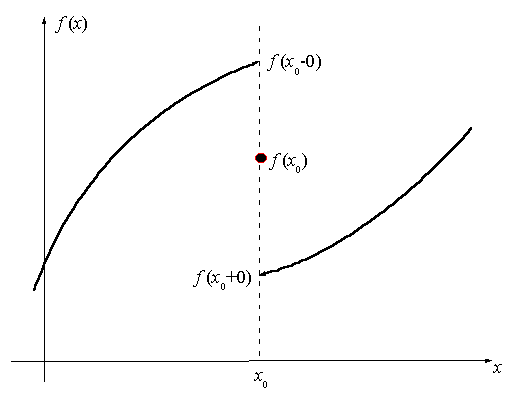
Рис. 2.2 Вид разрыва первого рода.

3. Разрыв второго рода.

Если хотя бы один из и равен ¥± или не существует, то говорят, что функция f(x) имеет в точке x₀ разрыв второго рода.

Вид разрывов второго рода очень разнообразен. Пример такого разрыва приведен на рис. 2.3. На нем изображен случай, когда f(x₀ – 0) конечен, а f(x₀ + 0) равен +¥.

Рис. 2.3. Пример разрыва второго рода.

2.3                 Свойства непрерывных функций

Теорема. Если f(x) и g(x) непрерывны в точке x₀, то в этой же точке непрерывны и функции f(x) ± g(x), f(x) × g(x) и f(x)/g(x) (последнее только в случае, если g(x₀)¹0).

Определение. Пусть y = f(x) и x = j(t). Тогда комбинация y = f(j(t)) называется суперпозицией функций f(x) и j(t), или сложной функцией.

Теорема о непрерывности сложной функции.

Пусть x = j(t) непрерывна в точке t₀, а функция f(x) непрерывна в точке x₀ = j(t₀). Тогда функция y = f(j(t)) непрерывна в точке t₀.

Короче говоря, суперпозиция непрерывных функций есть также непрерывная функция.