МАТРИЦЫ И ДЕЙСТВИЯ НАД НИМИ

Прямоугольная таблица, составленная из m x n элементов aij (i = 1,m, j -1,n) некоторого множества, называется матрицей и записывается в виде

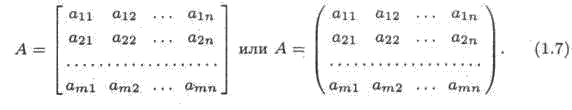
Элементы матрицы нумеруются 2 индексами. Первый индекс i эле­мента aij обозначает номер строки, а второй j — номер столбца, на пе­ресечении которых находится этот элемент в матрице. Матрицы обычно обозначают прописными буквами латинского алфавита: А, В, С,.. . Если у матрицы m строк и n столбцов, то по определению она имеет раз­мерность m x n. В случае необходимости это обозначается следующим образом:

Аm x n. Матрица называется числовой, если ее элементы aij — числа; функциональной, если aij — функции; векторной, если aij — век­торы, и т.д. Матрицы А и В называются равными, если все их соот­ветствующие элементы aij и bij равны, т.е. aij = bij. Следовательно, равными могут быть только матрицы одинаковой размерности. Матри­цы, у которых т = п, называются квадратными. Если i -1, то получаем матрицу-строку; если j =1, имеем матрицу-столбец. Их также называют вектор-строкой и вектор-столбцом соответственно.

Перечислим основные операции над матрицами.

1. Сложение и вычитание матриц. Эти операции определяются только для матриц одинаковой размерности. Суммой (разностью) ма­триц А и В, обозначаемой А + В (А — В), называется матрица С, эле­менты которой Cij == aij =b bij, где aij и bij — соответственно элементы матриц А и В. Например, пусть

Тогда

2. Умножение матрицы на число. Произведением матрицы А и числа А, обозначаемым А А, называется матрица В той же размерности, элементы которой bij = Аа^, где aij — элементы матрицы А, т. е. при умножении матрицы на число (числа на матрицу) надо все элементы матрицы умножить на это число. Например, пусть

3. Умножение матриц. Произведением матриц Am x n и Bn x p на­зывается матрица

Сm x p = А • В (или проще АВ), элементы которой Cij = ∑ⁿ_k=1 aikbkj, где aik>bkj — элементы матриц А и В. Отсюда следует, что произведение АВ существует только в случае, когда первый множитель А имеет число столбцов, равное числу строк второго множи­теля В. Далее, число строк матрицы АВ равно числу строк А, а число столбцов — числу столбцов В. Из существования произведения АВ не следует существование произведения ВА. В случае его существования, как правило, ВА≠АВ. Если АВ — В А, то матрицы А и В называются перестановочными (или коммутирующими). Известно, что всегда (АВ)С = А(ВС).

ОПРЕДЕЛИТЕЛИ И ИХ СВОЙСТВА.

ВЫЧИСЛЕНИЕ ОПРЕДЕЛИТЕЛЕЙ

Определителем n-гo порядка называется число ∆n, записываемое в виде квадратной таблицы

и вычисляемое, согласно указанному ниже правилу, по заданным чис­лам aij (i,j = 1, n), которые называются элементами определителя (всего их n²). Индекс i указывает номер строки, aj — номер столбца квадратной таблицы (1.1), на пересечении которых находится элемент aij. Любую строку или столбец этой таблицы будем называть рядом.

Главной диагональю определителя называется совокупность элемен­тов

a_11, a_{22,… .} Минором Mij элемента aij называется определитель (n — l)-гo по­рядка ∆n-i, полученный из определителя n-гo порядка ∆n вычеркива­нием г-й строки и j-гo столбца.

Алгебраическое дополнение Aij элемента aij определяется равен­ством

Aij = (-l)^i+j Mij

Значение определителя ∆n находится по следующему правилу.

Для n = 2

Для n = 3

Величины A₁₁,A₁₂,A₁₃ — алгебраические дополнения, а M₁₁,M₁₂, M₃₃ — миноры определителя ∆з, соответствующие его элементам a₁₁, a₂₂,a₃₃. Эти миноры являются определителями второго порядка, полу­чаемыми из определителя ∆з вычеркиванием соответствующих строки и столбца. Например, чтобы найти минор Mi2, следует в определителе ∆з вычеркнуть первую строку и второй столбец. Для произвольного n

где A_1k = (-l)^1+M_1k а миноры M_1k, являющиеся определителями (n - l)-гo порядка, получаются из ∆n вычеркиванием первой строки и k−го столбца. Например,

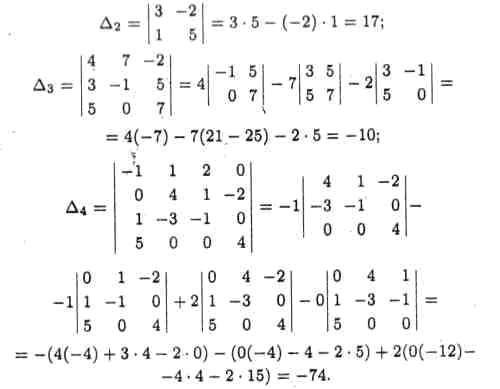
Замечание. Если элементами определителя являются некоторые функции, то данный определитель, вообще говоря, тоже функция (но может быть и числом). Например,

Правило вычисления определителя ∆з равносильно правилу тре­угольников (правилу Cappюca):

Схематическая запись этого правила приведена ниже:

Например,

Перечислим основные свойства определителей:

1) сумма произведений элементов любого ряда определителя и их алгебраических дополнений не зависит от номера ряда и равна этому определителю:

Эти равенства можно было бы (как и формулу (1.4)) принять за правило

вычисления определителя. Первое из них называется разложением ∆∏ по элементам %-й строки, а второе — разложением ∆n по элементам j-гo столбца;

2) значение определителя не меняется после замены всех его строк соответствующими столбцами, и наоборот;

3) если поменять местами два параллельных ряда определителя, то он изменит знак на противоположный;

4) определитель с двумя одинаковыми параллельными рядами равен нулю;

5) если все элементы некоторого ряда определителя имеют общий множитель, то последний можно вынести за знак

определителя. Отсюда следует, что если элементы какого-либо ряда умножить на число λ, то определитель ∆n умножится на это же число λ;

6) если все элементы какого-либо ряда определителя равны нулю, то определитель также равен нулю;

7) определитель, у которого элементы двух параллельных рядов со­ответственно пропорциональны, равен нулю;

8) сумма всех произведений элементов какого-либо ряда определи­теля и алгебраических дополнений соответствующих элементов другого параллельного ряда равна нулю, т. е. верны равенства:

9) если каждый элемент какого-либо ряда определителя представля­ет собой сумму двух слагаемых, то такой определитель равен сумме двух определителей, в первом из которых соответствующий ряд состоит из первых слагаемых, а во втором — из вторых слагаемых:

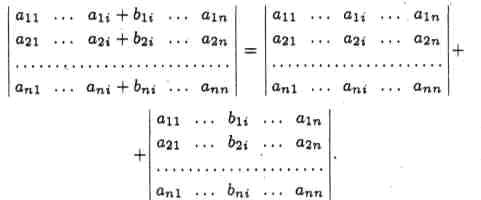
Например,

10) определитель не изменится, если ко всем элементам какого-либо его ряда прибавить соответствующие элементы другого параллельного ряда, умноженные на одно и то же произвольное число Л. Например, для столбцов определителя это свойство выражается равенством

Рассмотрим основные методы вычисления определителей.

1. Метод эффективного понижения порядка. В соответствии со свойством 4 вычисление определителя n-гo порядка сводится к вычисле­нию n определителей (n - l)-гo порядка. Этот метод понижения порядка не эффективен. Используя основные свойства определителей, вычисле­ние ∆n ≠ 0 всегда можно свести к вычислению одного определителя (n — l)-гo порядка, сделав в каком-либо ряду ∆n все элементы, кроме одного, равными нулю, покажем это на примере. Пример 1. Вычислить определитель

► ∏о свойству 5 определителей из первой строки вынесем множитель 10, а затем будем последовательно умножать полученную строку на 3, 1, 2 и складывать соответственно со второй, третьей и четвертой строками. Тогда, согласно свойству 10, имеем:

∏о свойству 1 определителей (см. второе из равенств (1.6)) полу­ченный определитель молено разложить по элементам второго столбца. Тогда

Получили определитель третьего порядка, который молено вычис­лить по правилу Cappюca или подобным же приемом свести к вычисле­нию одного определителя второго порядка. Действительно, вычитая из второй и третьей строк данного определителя первую строку, получаем:

2. Приведение определителя к треугольному виду. Определитель, у которого все элементы, находящиеся выше или ниже главной диагонали, равны нулю, называется определителем треугольного вида. Очевидно, что в этом случае определитель равен произведению элементов его глав­ной диагонали. Приведение любого определителя ∆n к треугольному виду всегда возможно.

Пример 2. Вычислить определитель

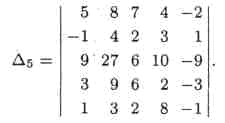
► Выполним следующие операции. Пятый столбец определителя сло­жим с первым, этот же столбец, умноженный на 3, — со вторым, на 2 — с третьим, на 8 — с четвертым столбцом. В итоге получим определитель треугольного вида, который равен исходному:

Приведение определителей к треугольному виду будет использовать­ся в дальнейшем при решении систем линейных уравнений методом Жopдaнa — Гаусса (его называют также методом Гаусса).

11 Метод Гаусса

2-этапа

1 Прямой ход Гаусса: последовательное исключение неизвестных из систем испозуются 3 преобразования оставляющие систему эквивалентнай

-перестановка местами уравнений

-умножение обеих частей урав. На произвольное число не=0

-прибавление к уравнению другого уравн. Умноженного на произвольное число

2 Обратный ход : находим неизвестные системы.

Если к системе прибавить свободный член то матрица называется расшыренной

Прямой ход Гаусса удобно проводить с расшыренной матрицей, работая только со строками.

Матрица приводится к трапецевидному виду в результате Прямого хода Гаусса

следующие вариант

в последнем ходе уравнения остается одна неизвестная – система имеет одно решение.

в последнем ходе уравнения остается две или более неизвестных – система имеет бесконечное множество решений.

12 Однородные системы линейных уравнений и их решение

Это система во всех уравнениях которых свободные члены равны 0

Всегда совмесна.

Не 0 решения одноредной системы имеет в случае ранг меньше неизвестных решения будет бесконечное множество .нужно выделить фундаментальную систему решений.

Число неизвестных минус ранг=число фундаментальных решений

Так как Однородные системы являются частным случаем то ее можно решать:Метод Гаусса. Метод исследования.

16.Скалярное произведение векторов.

Скалярным произведением векторов наз.произведение их модулей на косинус угла между ними. a*b=/a/*/b/*cos

Свойства:1.a*b=b*a 2.(*a)*b=a*(*b)= *a*b 3.(a+b)*c=a*c+b*c

a*b=x1*x2+y1*y2+z1*z2

доказательство: a(x1,y1,z1),b(x2,y2,z2)

a=x1i+y1j+z1k

b=x2i+y2j+z2k

a*b=( x1i+y1j+z1k)*( x2i+y2j+z2k) =x1*x2*i*i+x1y2*i*j+x1*z2*i*k+y1*x2*j*i+y1*y2*j*j+y1*z2*j*k+z1*x2*k*i+z1*y2*k*j+z1*z2*k*k=x1*x2+y1*y2*z1*z2

i*i=/i/*/i/*cos0=1

i*j=/i/*/j/*cosп/2=0

применение скалярного произведения векторов:

1.угол между векторами

2.ортогональность векторов (равенство нулю скаляр.произв.векторов явл. необход. и достаточным условием ортогональности векторов) a*b=0 – условие перпендикулярности

x1x2+y1y2+z1z2=0

3.вычисление проекции вектора

4.скаляргый квадрат вектора

а*а=а- скалярный квадрат

а=а*а=/а//а/cos0=/a/

5.направляющие косинус вектора

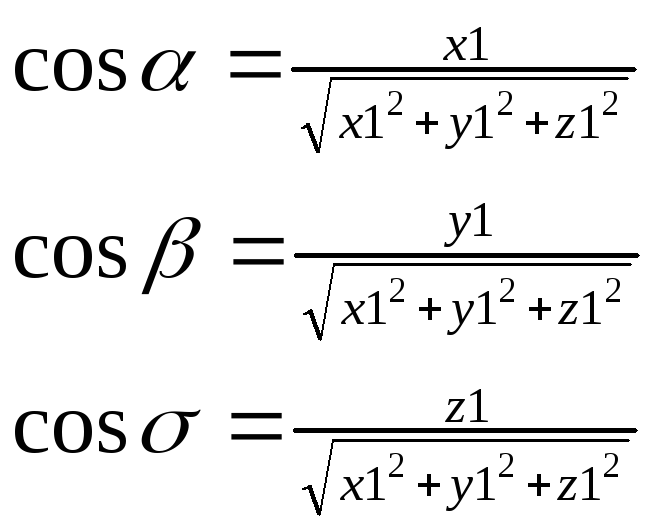
6.периодическая работа

17. Векторное произведение векторов.

Тройка векторов a,b,c наз.правой(левой) тогда, когда из конца 3-го вектора кратчайший поворот от 1-го ко 2-му происходит против часовой(по часовой) стрелки.

Векторным произв.двух векторов и наз. вектор удовлетворяющий следующим условиям:

Свойства:

Геометрический смысл модуля векторного произведения:

- модуль векторного произведения

Модуль векторного произведения векторов a и b равен площади параллелограмма построенного на этих векторах.

Из определения вектор. произв. следует, что если угол ,то модуль векторного произведения равен нулю.

-условие колинеарности векторов (параллельности)

Вывод: равенство нулю векторного произведения есть необходимое и достаточное условие колинеарности.

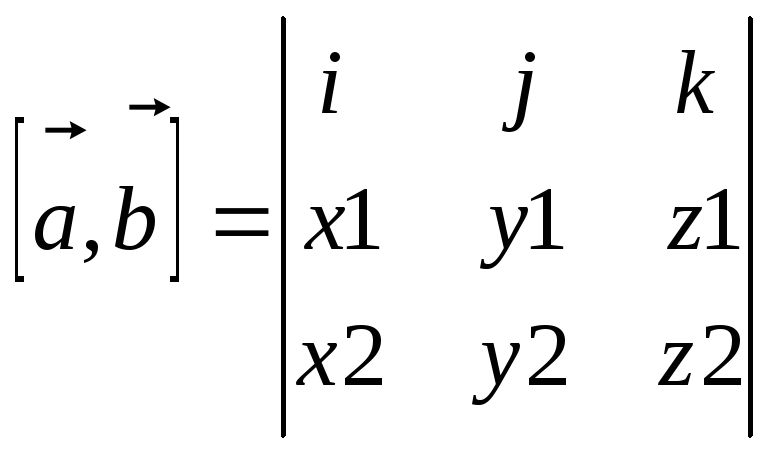
Применение векторного произведения:

1. Площадь параллелограмма или треугольника. Эта задача решается на основе геометрического смысла модуля векторного произведения. Для вычисления 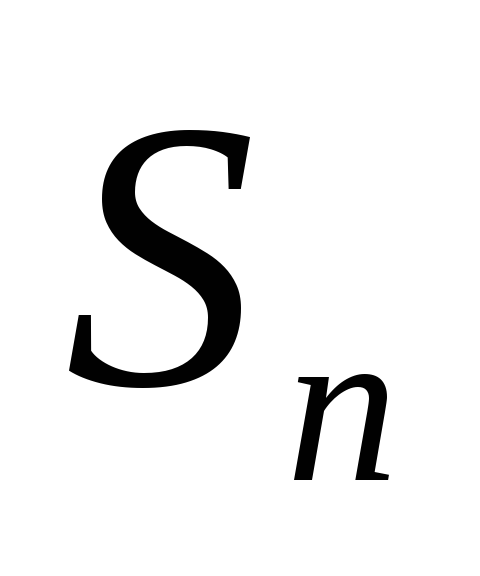необходимо вычислить соответственное векторное произведение и найти его модуль. В случае треугольника, его площадь равна половине площади параллелограмма.

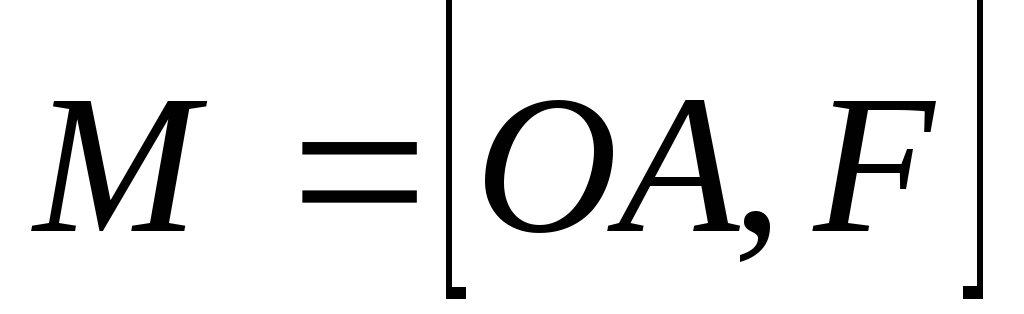2. Момент силы , момент силы F относительно точки О.