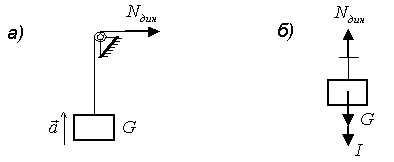5. Динамическое действие нагрузки

Динамическая нагрузка – это нагрузка, быстро меняющая свое значение и местоположение (например, движущийся поезд). Важнейшим признаком динамического воздействия служит появление в элементах конструкций сил инерции, сопоставимых по величине с внешними воздействиями.

С силами инерции связаны дополнительные напряжения и деформации, которые могут превысить напряжения и деформации от статической нагрузки. В расчетах влияние динамических нагрузок учитывается динамическим коэффициентом.

Сначала динамическая нагрузка заменяется статической и от ее действия определяются напряжения и деформации, которые затем умножаются на динамический коэффициент.

Рассмотрим два случая динамического воздействия: расчет на прочность при движении тела с постоянным ускорением и приближенное решение задачи на удар.

1. Поступательное движение тела с постоянным ускорением.

Груз G поднимается с постоянным ускорением а (Рис. 2.7.а). Определим динамическое усилие, возникающее в тросе (весом троса пренебрегаем).

Рис.2.7

К телу, кроме веса, по принципу Даламбера, должна быть приложена сила инерции , (где m – масса тела), направленная в сторону, противоположную ускорению (Рис. 2.7.б). Тогда

,

где g – ускорение силы тяжести.

Динамический коэффициент при постоянном ускорении

.

Статическое усилие в тросе было бы N_ст= G.

2. Ударное действие нагрузок.

Под ударом понимается взаимодействие движущихся тел в результате их соприкосновения, связанное с резким изменением скоростей движения точек этих тел за весьма малый промежуток времени.

Период соударения обычно очень мал и измеряется микро- или миллисекундами. Во время удара между соприкасающимися телами возникают весьма большие взаимные давления Р_д. Эти силы вызывают напряжения в обоих телах. Таким образом, в ударяемом теле возникают такие напряжения, как будто к нему приложена сила инерции ударяющего тела. Мы могли бы их вычислить, рассматривая силу инерции Р_д как статическую нагрузку. Затруднение заключается в определении этой силы инерции, так как мы не знаем продолжительности удара, то есть времени, за которое происходит изменение скорости. Значит, остается неизвестным ускорение.

Для вычисления Р_д приходится использовать закон сохранения энергии.

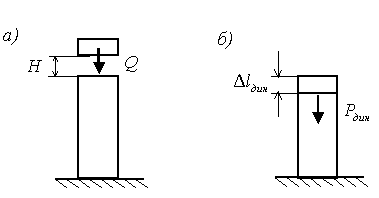
Рассмотрим случай продольного упругого удара (рис.2.8.а).

При ударе кинетическая энергия Т ударяющего тела превращается в потенциальную энергию U упругой деформации ударяемого тела

.

Рис.2.8

Кинетическая энергия ударяемого тела может быть вычислена так

(2.33)

В основе теории удара лежит гипотеза о том, что эпюра перемещений системы от груза Q при ударе подобна эпюре перемещений, возникающих от того же груза при его статическом действии. Согласно этой гипотезе потенциальная энергия, накопленная в ударяемом теле, определится по формуле

(2.34)

Приравняем правые части формул (2.33) и (2.34)

Так как (здесь – деформация от статически приложенной силы Q, - динамический коэффициент), то

При внезапном приложении груза (Н=0) k_д=2.

В случае поперечного удара коэффициент динамики вычисляется по аналогичной формуле где v_ст - статический прогиб балки в месте падения груза, вызванный действием силы, равной весу падающего груза.