2. Определение перемещений в балках.

В балках под нагрузкой происходит искривление оси, в результате чего возникают вертикальные перемещения v (прогибы) точек оси и углы поворота поперечных сечений (рис. 2.2).

Для определения прогибов v(z) и углов поворота применяются метод начальных параметров и интеграл Мора.

Рис.2.2

1. Метод начальных параметров.

Непосредственно из рассмотрения рис.2.2 в предположении малости углов поворота () следует связь между величинами v(z) и

(2.14)

Производная от функции угла поворота по координате оси балки определяет кривизну изогнутой оси

(2.15)

Кривизна связана с функцией изгибающего момента M_x зависимостью

(2.16)

где ‑ изгибная жесткость балки.

Комбинирование формул (2.15) и (2.16) приводит к выражению, известному как приближенное дифференциальное уравнение изогнутой оси стержня

(2.17)

В результате двукратного интегрирования уравнения (2.17) имеем

(2.18)

где v_{0 ,} - постоянные интегрирования, соответствующие прогибу и углу поворота начального сечения балки.

Функция прогибов для балки с несколькими участками записывается в виде

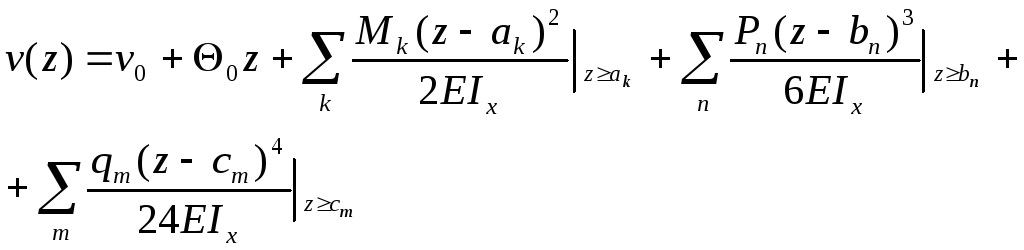(2.19)

где a_k,, b_n– координаты точек приложения сосредоточенных моментовM_k и сил P_n , _, c_m - координата начала приложения распределенной нагрузки q_m.

Функция угла поворота, согласно формуле (2.14), определяется дифференцированием функции прогибов и для балки с несколькими участками имеет вид

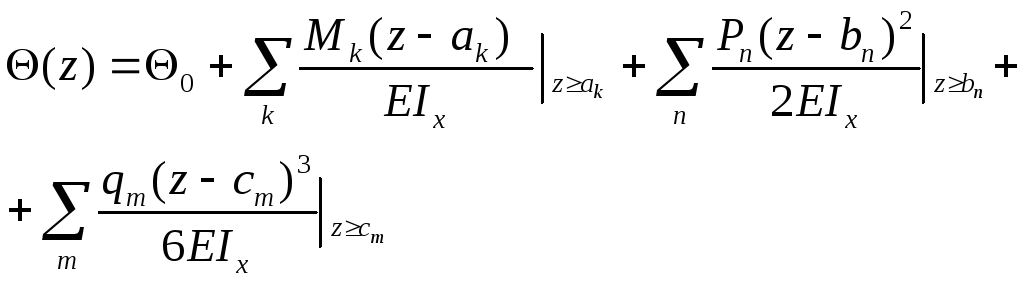(2.20)

Пример 1. Имеется однопролетная балка с консолью (рис.2.3). Требуется определить прогиб свободного края консоли (сечение А) и угол поворота опорного сечения В методом начальных параметров. В расчете принимается изгибная жесткость балки равная .

Вертикальные реакции опор и одинаковые и равны .

Рис.2.3

Правило знаков: положительным прогибам соответствуют перемещения точек оси балки вертикально вниз; с учетом зависимости (2.14), положительному углу поворота соответствует поворот касательной, проведенной к оси балки в заданном сечении, по часовой стрелке.

Искомый прогиб определяется по формуле (2.19), в которой следует принять (прогиб на шарнирной опоре равен нулю),

, ,

Неизвестный начальный угол поворота определяется из граничного кинематического условия (кинематическое граничное условие – уравнение, составленное для определения перемещений любого сечения балки с известным значением прогиба или угла поворота);

при

После определения начального угла поворота вычисляется прогиб сечения А.

Примечание. Распределенная нагрузка q, показанная на рис.2.3 пунктиром, вводится в тех случаях, когда прогиб определяется в сечении, которое находится за пределами участка действия распределенной нагрузки.

Угол поворота сечения В вычисляется по формуле (2.20), в которой следует принять