- •Кафедра "Прочность материалов и конструкций"
- •Программа курса.
- •Энергетические принципы, теоремы, методы в сопротивлении материалов
- •Расчет простейших статически неопределимых систем методом сил
- •Сложное сопротивление стержня
- •Устойчивость сжатых стержней
- •Динамическое действие нагрузок
- •Прочность материала при переменных напряжениях
- •Теоретические основы курса.
- •Сложная деформация.
- •Косой изгиб
- •Внецентренное растяжение-сжатие.
- •Изгиб с кручением.
- •Определение перемещений в балках.
- •Метод начальных параметров.
- •Интеграл Мора.
- •Статически неопределимые балки (Метод сил раскрытия статической неопределимости)
- •Устойчивость сжатых стержней
- •Динамическое действие нагрузки
- •Поступательное движение тела с постоянным ускорением.
- •Ударное действие нагрузок.
- •Задания на контрольные работы с примерами решения.
- •Задача 6 "Косой изгиб стержня"
- •Построение эпюр усилий.
- •Вычисление осевых моментов сопротивления
- •Подбор размеров поперечного сечения балки.
- •Задача 7 "Внецентренное сжатие стержня большой изгибной жесткости"
- •Уравнение нейтральной оси при внецентренном растяжении – сжатии имеет вид
- •Через центры фигур разбиения проводятся оси и . Вычисляются собственные моменты инерции фигур ,
- •Подстановка полученных результатов в формулы (3.3) и (3.4) дает
- •Задача 8 "Статически неопределимые балки"
- •Пример решения задачи
- •Раскрытие статической неопределимости задачи.
- •Для вычисления коэффициентов канонического уравнения надо построить единичную и грузовую эпюры изгибающего момента.
- •Если в расчете величина получается отрицательной, то необходимо изменить знак эпюры по отношению к эпюре .
- •Оказывается, что такого значения в таблице нет. Ближайшими значениями осевого момента сопротивления являются:
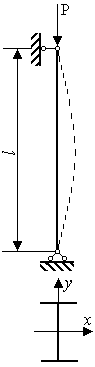
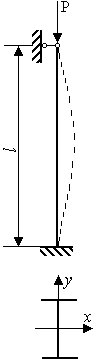
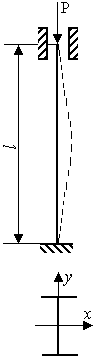
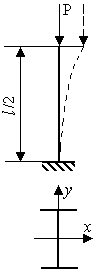
- •Задача 9 "Устойчивость центрально – сжатого стержня"
- •Исходные данные приведены в таблице 4.
- •Пример решения задачи
- •Определение грузоподъемности стержня. Грузоподъемность центрально сжатого стержня определяется по формуле
- •Подбор рационального поперечного сечения стержня.
- •Вычисляются нормальные напряжения
- •В результате решения данного квадратного уравнения определяется значение .
- •Лабораторный практикум
- •Лабораторная работа №5. "Определение реакции лишней связи в статически неопределимой балке"
- •Лабораторная работа № 6 "Определение величины критической силы центрально сжатого стержня".
- •Лабораторная работа № 7. "Ударная проба материала на излом"
- •Контрольные вопросы к зачету и экзамену2
- •Часть 2
- •Приложение 1
- •Приложение 2
- •Приложение 3 Коэффициент продольного изгиба φ
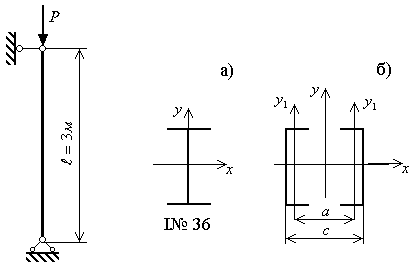
Пример решения задачи
Исходные данные приведены на рис. 3.11.
-
Определение грузоподъемности стержня. Грузоподъемность центрально сжатого стержня определяется по формуле
![]() ,
(3.19)
,
(3.19)
где
![]() – коэффициент понижения основного
допускаемого напряжения.
– коэффициент понижения основного
допускаемого напряжения.
Коэффициент
![]() зависит от
зависит от
![]() ,
то есть
,
то есть
![]() .
Гибкость вычисляется по формуле
.
Гибкость вычисляется по формуле
![]() ,
(3.20)
,
(3.20)
где
-
μ - коэффициент приведения длины стержня,
-
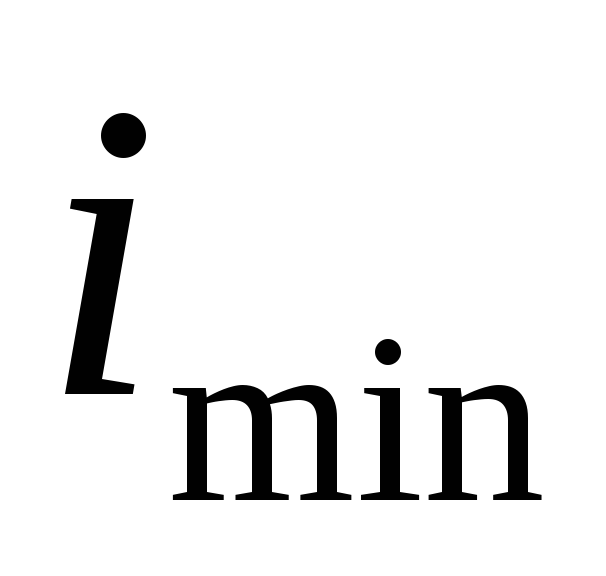 ‑ минимальный радиус инерции
поперечного сечения стержня
‑ минимальный радиус инерции
поперечного сечения стержня
Величина
![]() определяется по сортаменту "Балки
двутавровые" (Приложение 1). Для
заданного номера двутавра № 36 в
сортаменте находим
определяется по сортаменту "Балки
двутавровые" (Приложение 1). Для
заданного номера двутавра № 36 в
сортаменте находим
![]() ,
,
![]() ,
следовательно
,
следовательно
![]() .
При шарнирном опирании стержня коэффициент
приведения длины
.
При шарнирном опирании стержня коэффициент
приведения длины
![]() .
.
Гибкость стержня
![]() .
.
|
а) |
|||||
|
|
|
|
|
||
|
|
|
|
|
||
|
б) |
|||||
|
|
|
|
|||
|
|
|
|
|||
|
Рис.3.10 |
|||||
|
|
|
Рис.3.11 |
По таблице коэффициента продольного
изгиба (Приложение 3) для
![]() и стали марки Ст. 4, 3, 2 определяется
значение коэффициента
и стали марки Ст. 4, 3, 2 определяется
значение коэффициента
![]() понижения основного допускаемого
напряжения. В таблице зависимости
понижения основного допускаемого
напряжения. В таблице зависимости
![]() от
от
![]() значения гибкости кратны 10. Поэтому, из
таблицы берутся два ближайших к найденному
значения гибкости
значения гибкости кратны 10. Поэтому, из
таблицы берутся два ближайших к найденному
значения гибкости
![]() и соответствующие им два значения
и соответствующие им два значения
![]() :
:
![]() ,
,
![]()
![]() ,
,
![]() .
.
Для определения искомого
значения коэффициента
![]() выполняется линейная интерполяция:
выполняется линейная интерполяция:
![]()
Величина допускаемой нагрузки на устойчивость
![]()
где
-
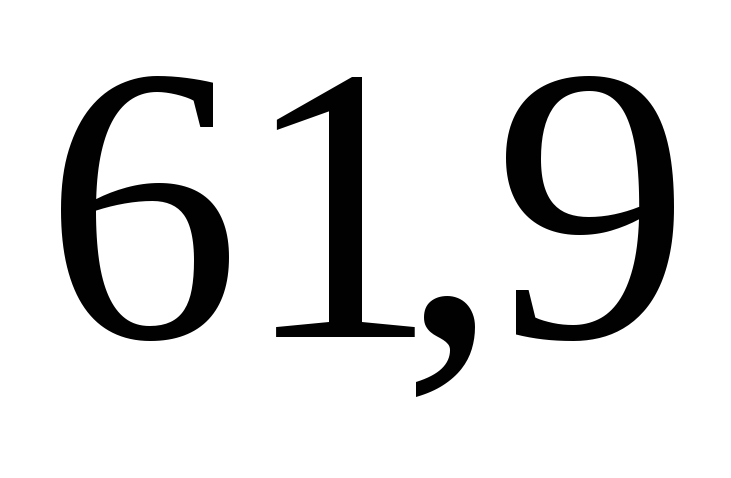 см2 ‑ площадь поперечного
сечения двутавра № 36 (берется по
сортаменту).
см2 ‑ площадь поперечного
сечения двутавра № 36 (берется по
сортаменту).
-
Подбор рационального поперечного сечения стержня.
Рациональным
поперечным сечением является сечение,
у которого главные моменты инерции
одинаковые
![]() .
У стандартных прокатных профилей моменты
инерции
.
У стандартных прокатных профилей моменты
инерции
![]() и
и
![]() значительно отличаются (например, для
двутавра I № 36
значительно отличаются (например, для
двутавра I № 36
![]() ,
,
![]() ).
В расчетах на устойчивость используется
минимальный момент инерции
).
В расчетах на устойчивость используется
минимальный момент инерции
![]() .
Максимальный момент инерции
.
Максимальный момент инерции
![]() ,
не используемый в расчетах на устойчивость,
косвенно свидетельствует о наличии
перерасхода материала.
,
не используемый в расчетах на устойчивость,
косвенно свидетельствует о наличии
перерасхода материала.
Рациональное
поперечное сечение может быть
сконструировано с помощью двух одинаковых
прокатных профилей. (рис. 3.11,б). Варьируя
значение величины а (или с), можно
для любого номера швеллера добиться
выполнения условия
![]() .
Момент инерции
.
Момент инерции
![]() двух швеллеров равен
двух швеллеров равен
![]() (
(![]() - осевой момент инерции швеллера,
определяется по номеру швеллера).
- осевой момент инерции швеллера,
определяется по номеру швеллера).
При подборе
рационального поперечного сечения
стержня, определенная ранее величина
допускаемой нагрузки
![]() ,
принимается в качестве исходной
,
принимается в качестве исходной
Формула (3.19) переписывается в виде
![]() (3.21)
(3.21)
В правую часть
формулы (3.21) входит коэффициент
![]() ,
который зависит от площади
,
который зависит от площади
![]() ,
так как
,
так как
![]() ,
а
,
а
![]() .
Такие уравнения решаются методом
последовательных приближений.
.
Такие уравнения решаются методом
последовательных приближений.
На первом шаге назначается среднее
значение коэффициента
![]() .
Подстановка
.
Подстановка
![]() в формулу (3.21) дает величину требуемой
площади поперечного сечения
в формулу (3.21) дает величину требуемой
площади поперечного сечения
![]() .
.
Площадь одного
швеллера
![]()
По сортаменту "Швеллеры"
(Приложение 2) по величине
![]() подбирается номер прокатного профиля,
площадь поперечного сечения которого
подбирается номер прокатного профиля,
площадь поперечного сечения которого
![]() ,
это швеллер [ № 27 (
,
это швеллер [ № 27 (![]() ,
,
![]() ).
).
Осевые моменты инерции
рационального поперечного сечения
одинаковые
![]() .
Вычисляется минимальный радиус инерции
рационального сечения
.
Вычисляется минимальный радиус инерции
рационального сечения
![]()
Определяется гибкость стержня
![]()
По таблице
"Коэффициент продольного изгиба
![]() "
(Приложение 3) для
"
(Приложение 3) для
![]() и материала Ст. 4, 3, 2 находится
и материала Ст. 4, 3, 2 находится
![]() .
Допускаемые напряжения на устойчивость
.
Допускаемые напряжения на устойчивость
![]() .
.