Пример решения задачи

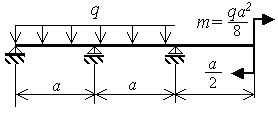
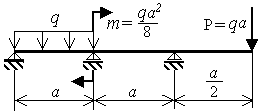
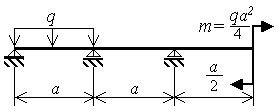
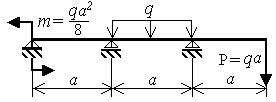
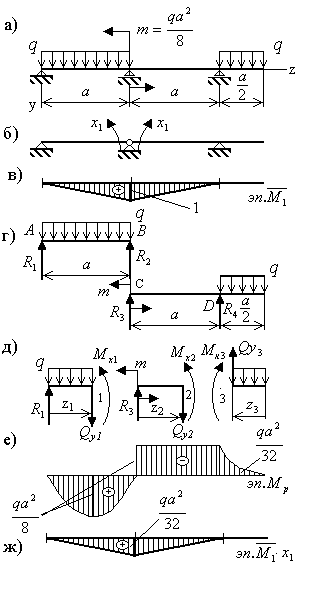
На рис. 3.9,а показана один раз статически неопределимая балка. Примем в расчете , .

1. Раскрытие статической неопределимости задачи.

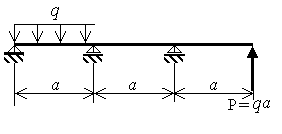
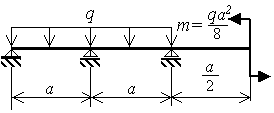
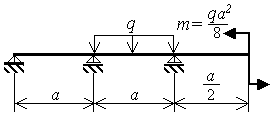
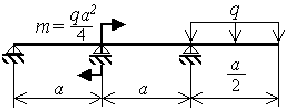
Согласно алгоритму метода сил на первом шаге решения задачи производится выбор основной системы (рис.3.9,б). Основная система получается из заданной путем отбрасывания лишней связи (внешней или внутренней). В рассматриваемом примере в балку "врезается" шарнир над средней опорой.

Неизвестный опорный момент определяется из канонического уравнения метода сил

(3.16)

где

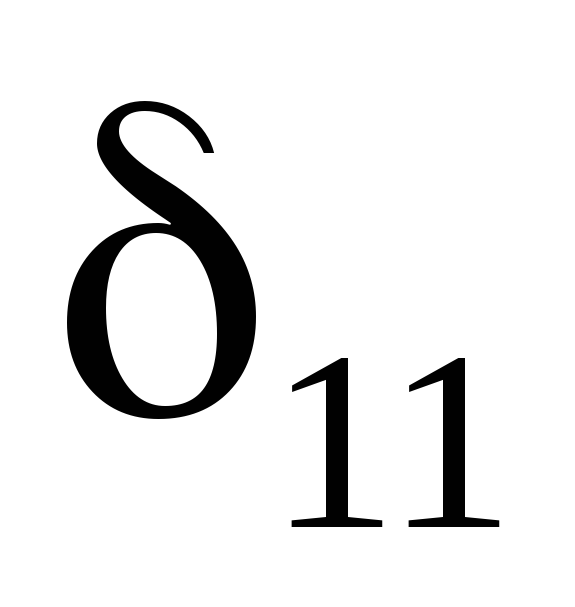• ‑ перемещение по направлению отброшенной связи, вызванное действием

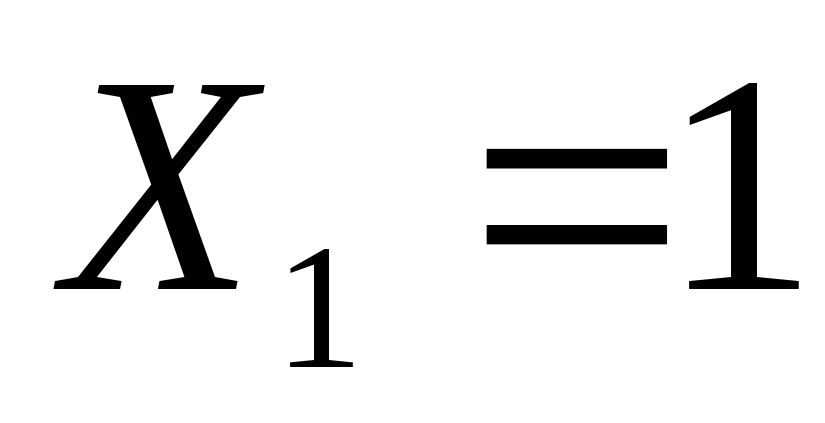
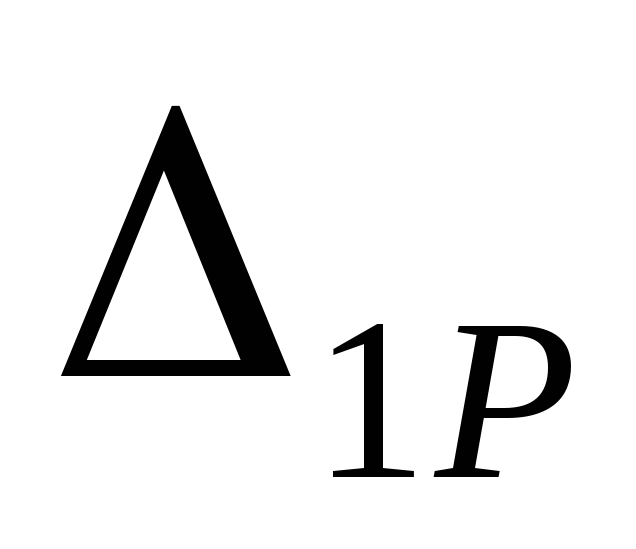• ‑ перемещение по направлению 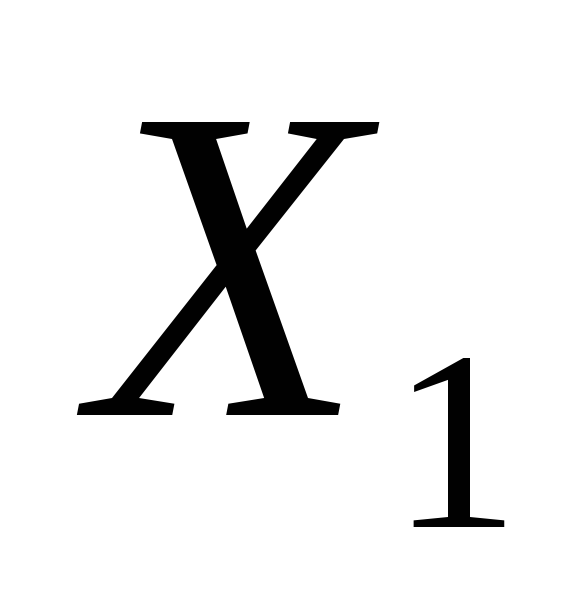, вызванное действием заданной нагрузки

Рис.3.8

Рис.3.9

Вычисление перемещений и производится по формуле Симпсона:

(3.17)

где

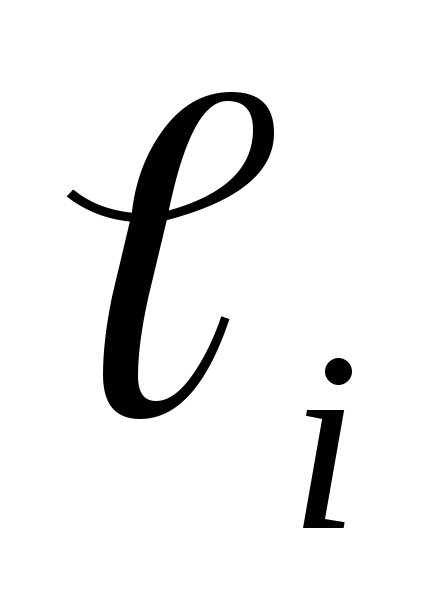• - длина участка перемножения эпюр;

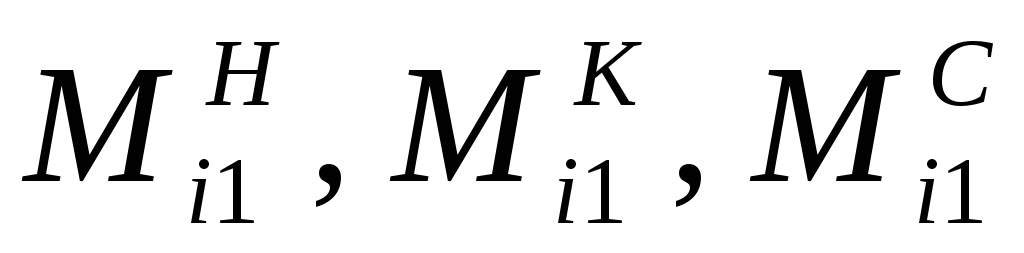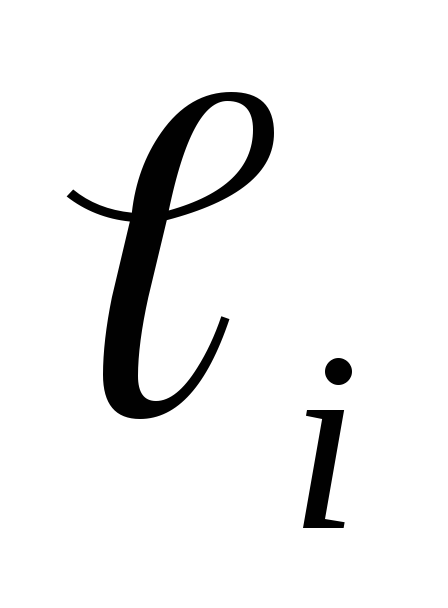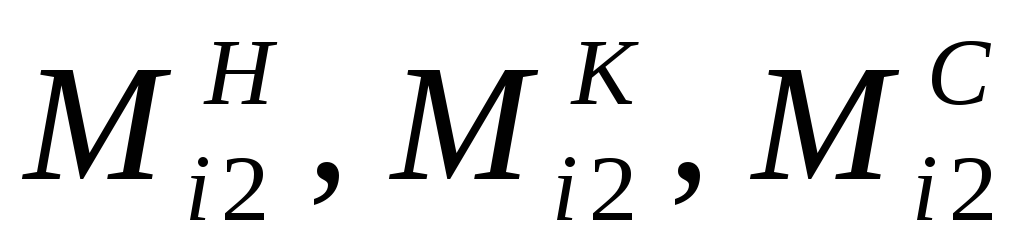• - ординаты первой эпюры изгибающего момента в начале, в конце и в середине участка ;

• , ‑ ординаты второй эпюры изгибающего момента в начале, в конце и в середине участка ;

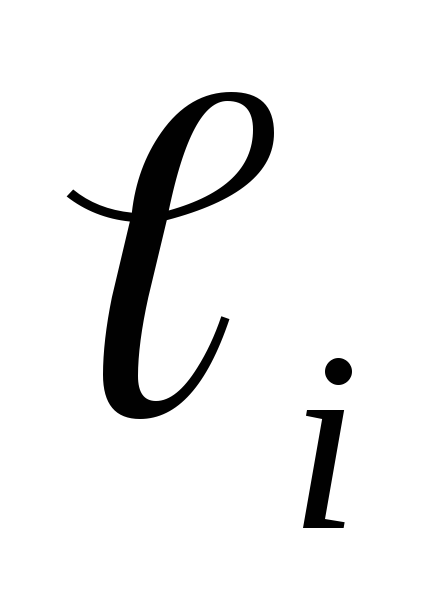Для вычисления коэффициентов канонического уравнения надо построить единичную и грузовую эпюры изгибающего момента.

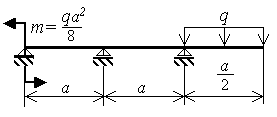
Построение единичной эпюры производится в основной системе (рис. 3.9,б) в предположении . Очертание единичной эпюры изгибающего момента приведено на рис. 3.9,в.

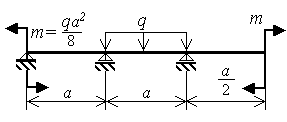
При построении грузовой эпюры удобно расчленить исходную балку на две балки и (рис.3.9,г). Членение балки производится в месте постановки шарнира.

Балка однопролетная, нагруженная равномерно распределенной нагрузкой интенсивностью . В силу симметрии реакции и одинаковые и равны . Балка имеет один участок, поэтому для построения эпюры изгибающего момента достаточно рассмотреть равновесие одной отсеченной части (рис.3.9,д)

Эпюра имеет параболическое очертание. В качестве третьей точки выбирается середина участка распределенной нагрузки, то есть

Очертание эпюры в балке приведено на рис.3.9,е.

Балка однопролетная с консолью.

Для определения реакций опор записываются уравнения равновесия

.

Для построения эпюры изгибающего момента в балке надо рассмотреть равновесие двух отсеченных частей (рис.3.9, д):

и ,

,

; ;

Очертание эпюры изгибающего момента в балке приведено на рис.3.9,е.

В

ычисление и .

Коэффициент вычисляется по формуле .

Единичная эпюра имеет три участка (один нулевой), поэтому перемножение эпюры производится по двум участкам:

вычисляется по формуле :

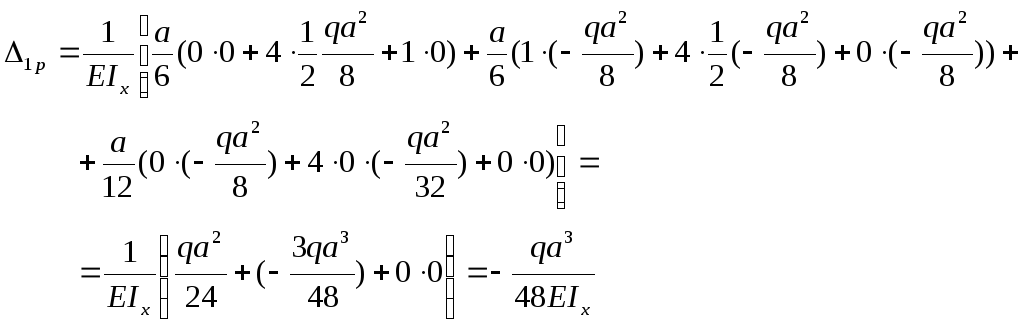
Вычисленные значения и подставляются в каноническое уравнение (3.16)

Ординаты эпюры изгибающего момента в статически неопределимой балке вычисляются по формуле

(3.18)

Эпюра изгибающего момента представляет собой исходную единичную эпюру, ординаты которой увеличены в раз (рис. 3.9,ж).