Уравнение нейтральной оси при внецентренном растяжении – сжатии имеет вид

, (3.8)

где

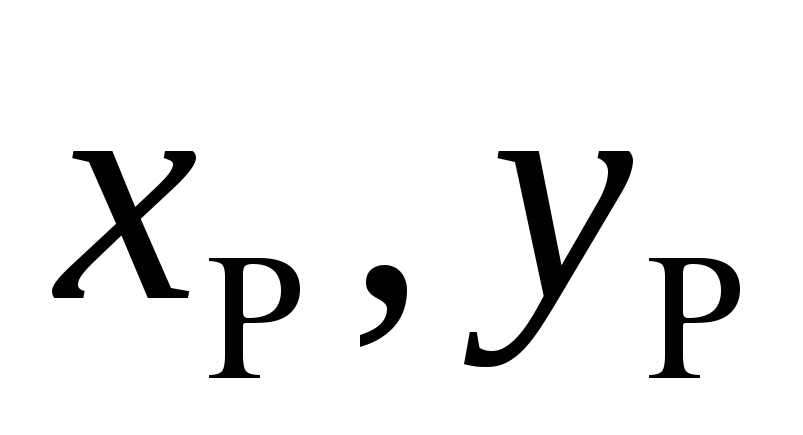• - координаты точки приложения силы Р,

• х, у - координаты точек нейтральной оси,

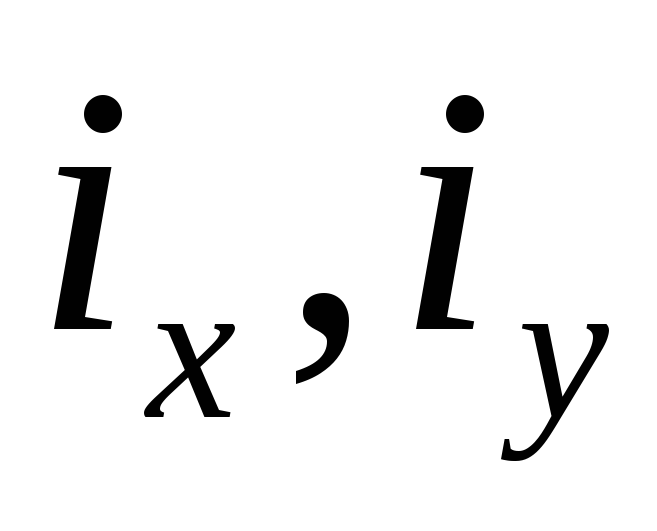• - радиусы инерции поперечного сечения стержня.

Рис.3.6

Радиусы инерции вычисляются по формуле

, (3.9)

Для вычисления осевых моментов инерции воспользуемся формулами (3.3) и (3.4)

(3.10)

(3.11)

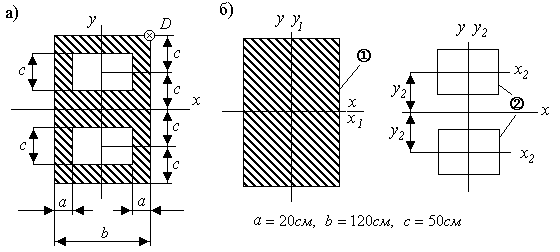
На рис. 3.6,б исходное поперечное сечение представлено в виде трех прямоугольников.

Через центры фигур разбиения проводятся оси и . Вычисляются собственные моменты инерции фигур ,

, , ,

Совпадение осей и x, а также и означает, что координаты и центров фигур разбиения равны нулю.

Подстановка полученных результатов в формулы (3.3) и (3.4) дает

(3.12)

(3.13)

Знак минус в формулах (3.12) и (3.13) связан с тем фактом, что фигуры разбиения 2 являются отверстиями. Подстановка в формулы (3.12) и (3.13) , и дает , . Площадь F поперечного сечения стержня или . Квадраты радиусов инерции поперечного сечения

, .

Уравнение нейтральной оси (3.8) принимает вид

(3.14)

Для построения нейтральной оси вычисляются координаты ее точек:

• при ,

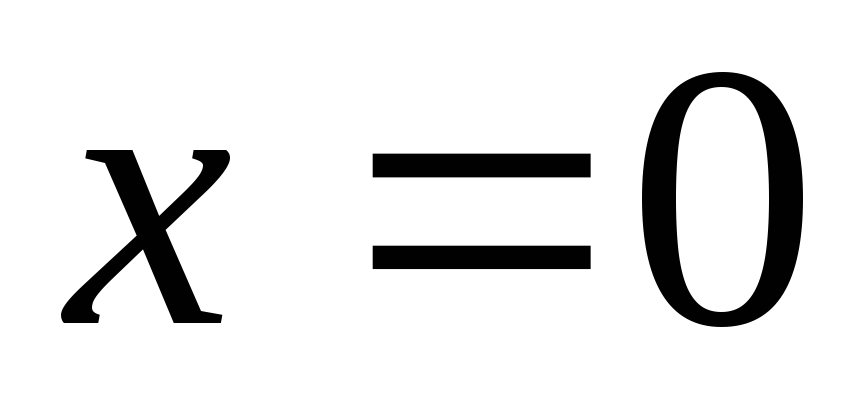
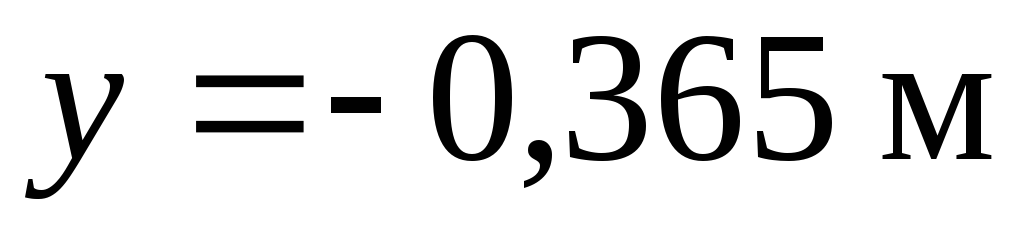• при .

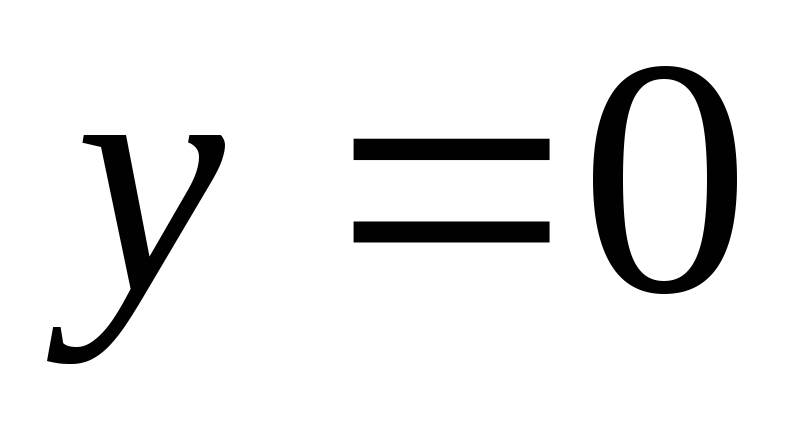
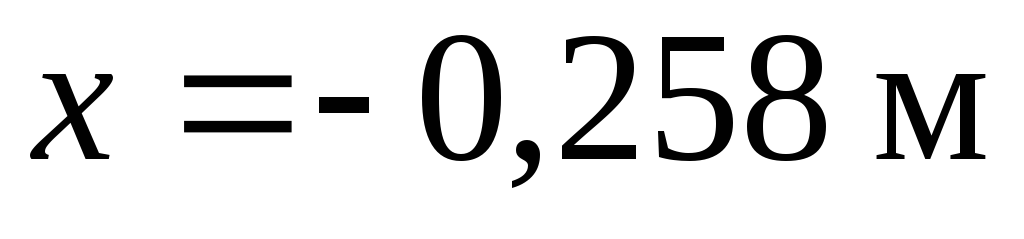Координаты (, ) и (, ) наносятся на чертеж сечения (рис.3.7), и через эти две точки проводится нейтральная ось.

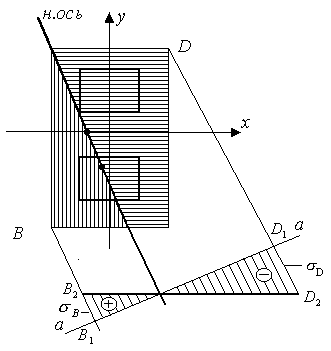
К нейтральной оси проводится перпендикулярный отрезок а-а, на котором строится эпюра нормального напряжения . Через наиболее удаленные от нейтральной оси точки В и D проводятся параллельно нейтральной оси отрезки ВВ₁ и DD₁. Далее в произвольном масштабе откладывается отрезок D₁D₂, определяющий напряжение в точке D. Через точку D₂ и нулевую точку нейтральной оси проводится отрезок, определяющий положение точки В₂. Отрезок В₁В₂, в выбранном масштабе, соответствует напряжению . Таким образом, в точке D сечения реализуются наибольшие сжимающие, а в точке В наибольшие растягивающие напряжения.

Рис.3.7

Величина допускаемой нагрузки определяется из условия прочности для внецентренного растяжения – сжатия.

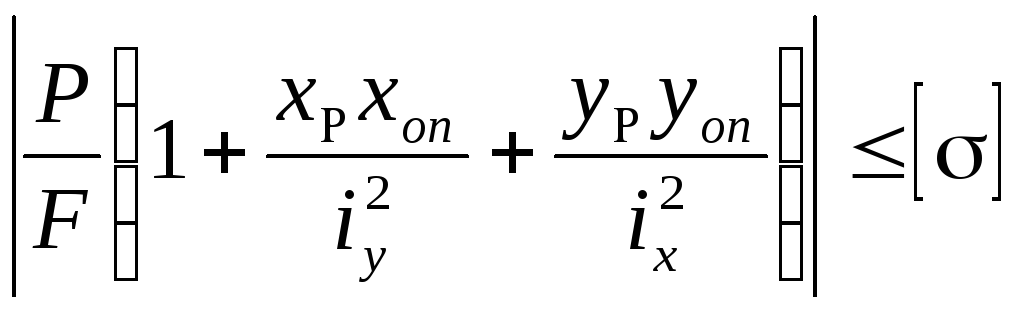, (3.15)

откуда

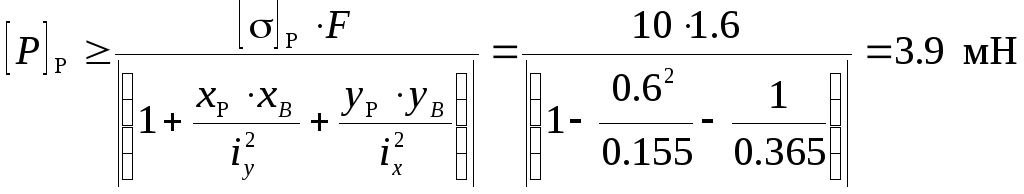
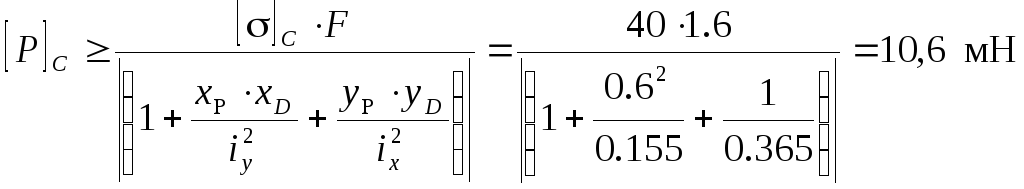
Таким образом, грузоподъемность стержня или

3. Задача 8 "Статически неопределимые балки"

Двухпролетная балка с консолью, нагружена равномерно распределенной нагрузкой интенсивностью q, силой Р и парами сил m (рис. 3.8)

Требуется:

1. Раскрыть статическую неопределимость задачи с помощью метода сил. Построить эпюру изгибающего момента.

2. Подобрать поперечное сечение балки в виде двутавра, приняв [] =160 МПа.

Исходные данные приведены в таблице 2.

Таблица 2

Номер схемы (рис.3.8)	1	2	3	4	5	6	7	8	9	0	А
а, м	6	7	8	9	10	11	12	10	8	6	В
q, кН/м	16	18	20	22	24	22	20	18	16	14	А
индекс	1	2	3	4	5	6	7	8	9	0