3. Подбор размеров поперечного сечения балки.

Условие прочности (3.1) переписывается в виде

(3.7)

В соответствии с исходными данными принимается

,

,

Вычисленные значения и подставляются в формулу (3.7)

.

Таким образом, подобраны размеры поперечного сечения заданной формы.

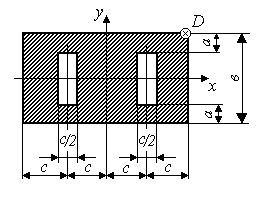
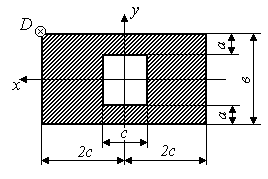
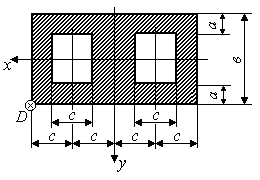
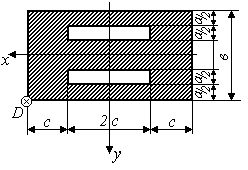
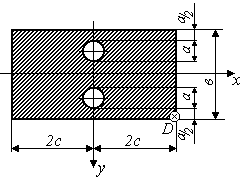
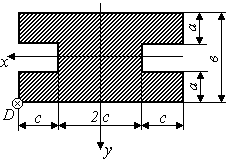
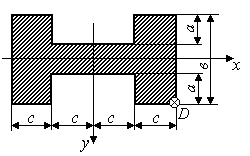
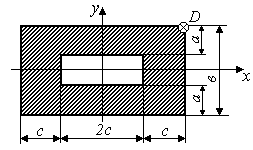
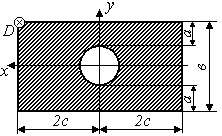
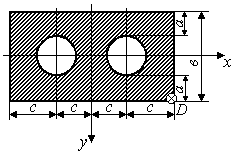
2. Задача 7 "Внецентренное сжатие стержня большой изгибной жесткости"

На стержень заданного поперечного сечения в точке D действует сжимающая сила Р (рис.3.5)

Требуется:

1. Вычертить в масштабе сечение стержня, показав положение главных центральных осей инерции.

2. Определить положение нейтральной линии и показать ее на схеме сечения.

3. Показать эпюру нормального напряжения 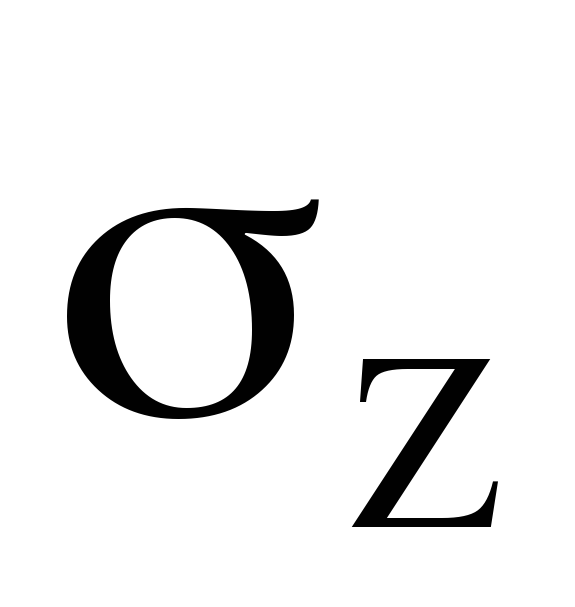и отметить в сечении положение опасных точек.

4. Определить величину допускаемой нагрузки, приняв , .

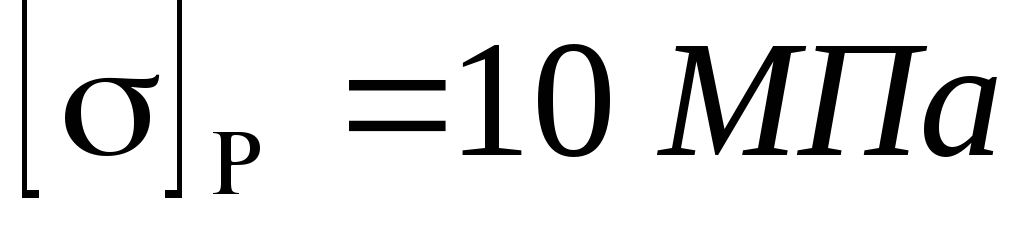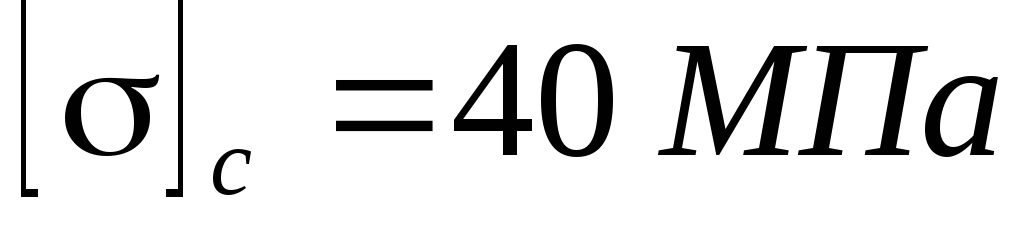Исходные данные приведены в таблице 1.

Таблица 1

Номер		b, см	с, см	а, см
строки	схемы (рис.3.5)
1	1	120	50	20
2	2	130	55	25
3	3	140	60	30
4	4	150	65	20
5	5	120	70	25
6	6	130	50	30
7	7	140	55	20
8	8	150	60	25
9	9	120	65	30
0	0	130	70	20
	А	В	А	В

Пример решения задачи.

Исходные данные приведены на рис. 3.6,а

Величина допускаемой нагрузки определяется из условия, что напряжение в наиболее нагруженной точке сечения достигает значения . В исходных данных задачи приведены два значения допускаемого напряжения, ‑ (допускаемое напряжение на растяжение) и (допускаемое напряжение на сжатие). Это означает, что материал стержня по разному сопротивляется растяжению и сжатию (факт, характерный для хрупких материалов). При решении задачи вычисляются два значения допускаемой нагрузки: - в предположении, что наибольшее растягивающее напряжение достигает значения и - в предположении, что наибольшее сжимающие напряжение достигает значения .

Из двух значений нагрузок , выбирается меньшая, для которой обеспечивается прочность материала по растягивающим и сжимающим напряжениям. Нормальные наибольшие растягивающие и сжимающие напряжения возникают в точках, наиболее удаленных от нейтральной оси.

Рис.3.5