лабораторная работа / лабар.№3

ЦЕЛЬ РАБОТЫ: получение навыков исследования линейных динамических моделей в программном пакете Matlab и ознакомление с временными и частотными характеристиками систем автоматического управления (САУ).

Задана передаточная функция САУ:

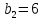
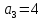
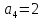
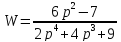
Задание 1.

Создадим LTI-объект с именем w, для этого выполним:

>> w=tf([6 0 -7],[2 4 0 0 9])

Transfer function:

6 s^2 - 7

-----------------

2 s^4 + 4 s^3 + 9

Задание 2.

Найдем полюса и нули передаточной функции с использованием команд pole, zero.

>> pole(w)

ans =

-1.6911 + 0.6773i

-1.6911 - 0.6773i

0.6911 + 0.9373i

0.6911 - 0.9373i

>> zero(w)

ans =

1.0801

-1.0801

Задание 3.

Построим переходную функцию командой step(w). Выполнения отобразить в виде графика.

>> step(w)

Рис.1 Переходная функция h(t)

Задание 4.

Построить импульсную переходную функцию командой impulse(w).

>> impulse(w)

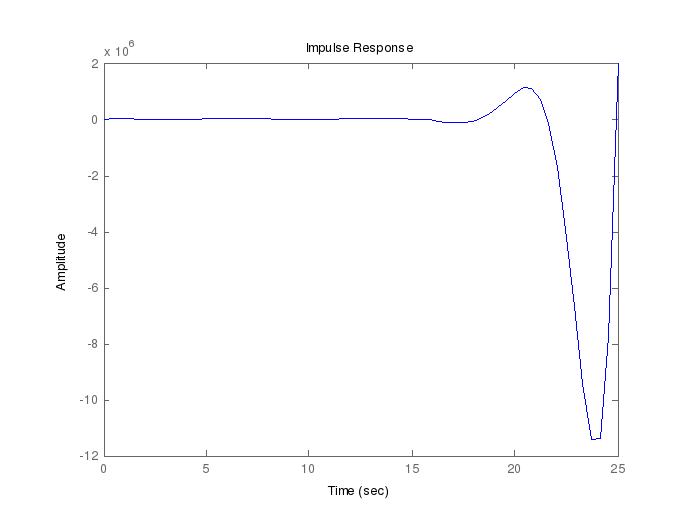
Рис.2 Импульсная переходная функция

Задание 5.

Диаграмму Боде получим, используя команду bode(w).

>> bode(w)

Рис.3 Логарифмические частотные характеристики

Задание 6.

Определим частотный годограф Найквиста, выполнив команду nyquist(w).

>> nyquist(w)

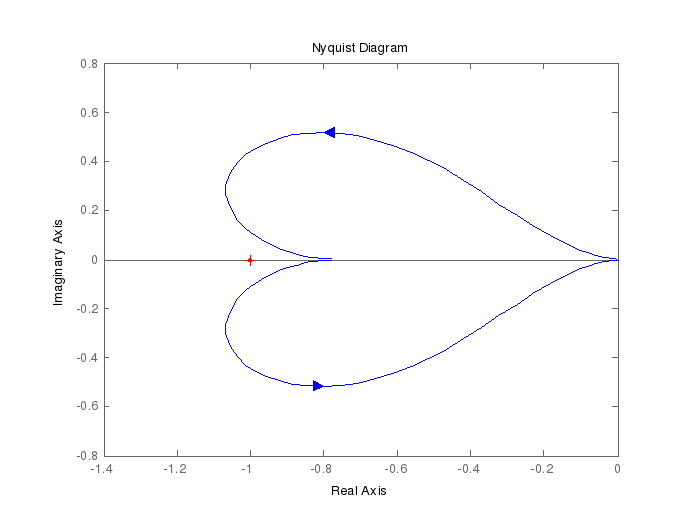
Рис.4 Частотный годограф

ВЫВОД: Провела исследование линейных динамических моделей и ознакомилась с временными и частотными характеристиками САУ, кроме того могу сделать вывод что система, согласно критерию Найквиста будет устойчивой, т.к. не охватывается точка с координатами (-1;0j).