- •Кафедра тк
- •1. Цель работы
- •2. Выполнение работы
- •2.1. Позиционные звенья
- •2.1.1. Апериодическое (инерционное) звено первого порядка
- •2.1.2. Апериодическое звено второго порядка
- •2.1.3. Колебательное звено второго порядка
- •Переходная
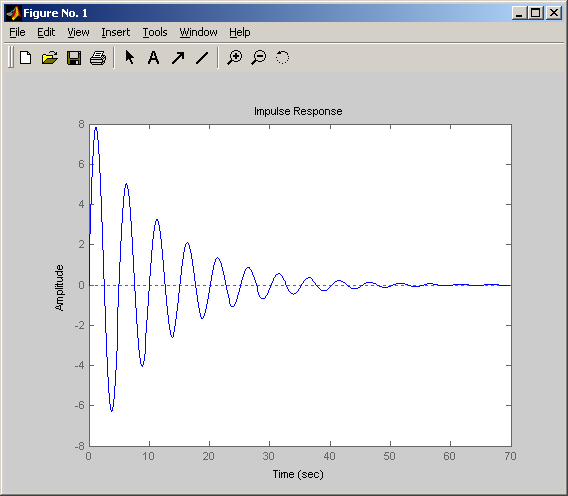
- •Весовая (импульсная переходная)
- •Логарифмическая амплитудная и фазовая частотные характеристики
- •Амплитудно-фазовая частотная характеристика
- •2.2. Интегрирующие звенья
- •2.2.1. Идеальное интегрирующее звено
- •2.2.2. Изодромное звено (пропорционально-интегрирующее звено)
- •2.3. Дифференцирующие звенья
- •2.3.1. Реальное дифференцирующее звено
- •2.3.2. Инерционно-форсирующее (реальное форсирующее) звено
- •3. Выводы
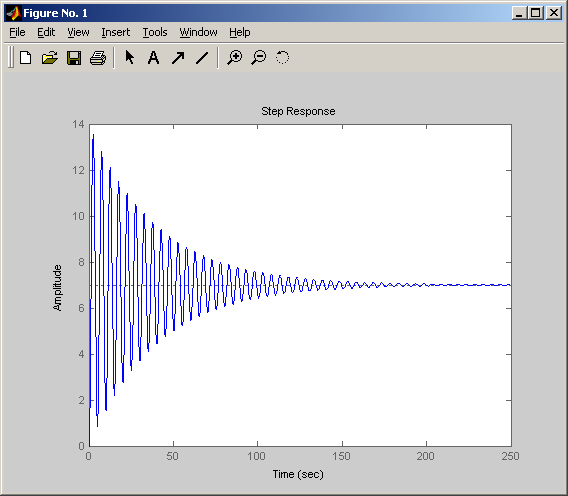
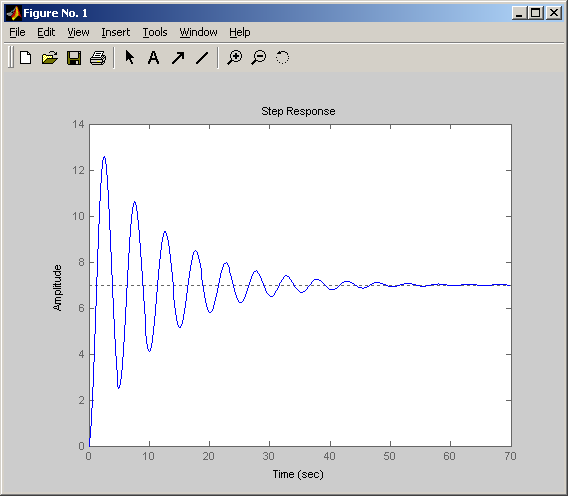
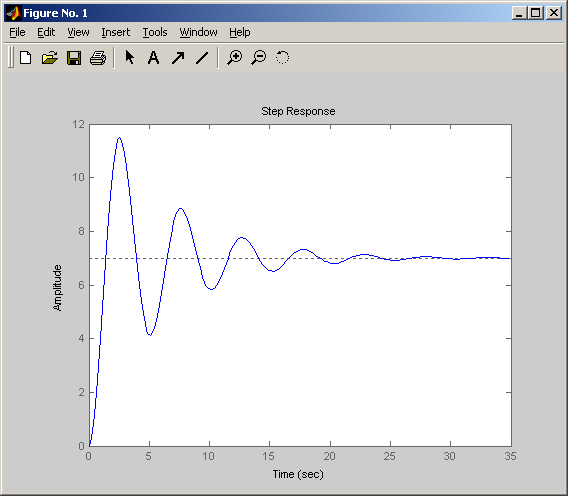
2.1.3. Колебательное звено второго порядка
Передаточная функция имеет вид
![]() (1)
(1)
![]()
Величина
![]() в (1) представляет частоту собственных
колебаний.
в (1) представляет частоту собственных
колебаний.
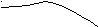
Временные характеристики
Переходная
![]()
![]()
![]()
Снижение параметра затухания ξ приводит к повышению колебательности переходного процесса.
Весовая (импульсная переходная)
Частотные характеристики
Логарифмическая амплитудная и фазовая частотные характеристики
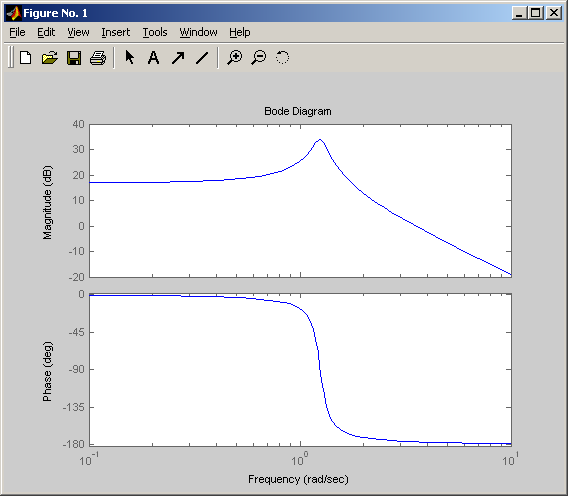
ЛАХ и ФЧХ при ξ=0,07
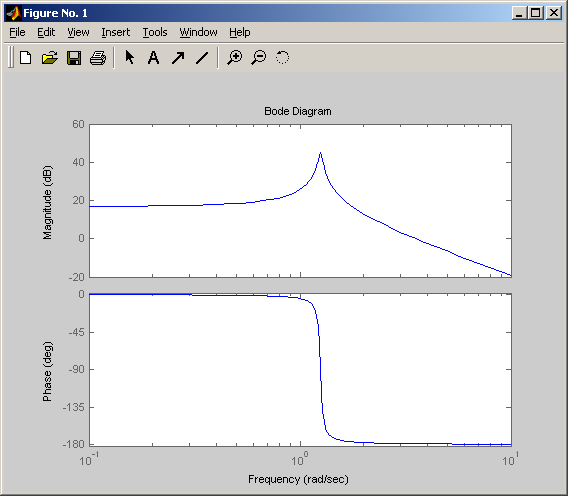
ЛАХ и ФЧХ при ξ=0,02
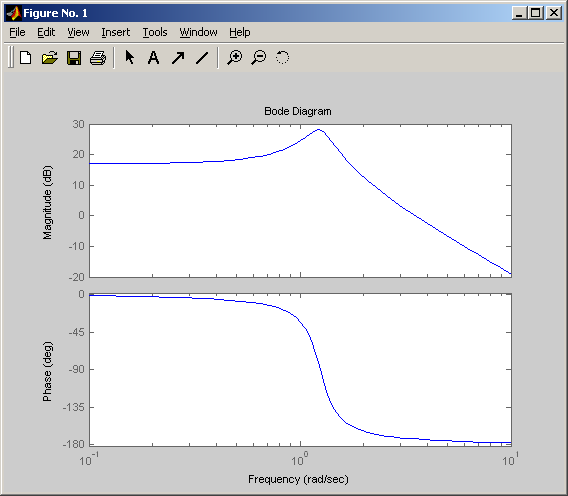
ЛАХ и ФЧХ при ξ=0,14
Снижение параметра затухания ξ приводит к росту резонансного пика ЛАХ.
Чем больше параметр ξ , тем более пологий будет график ЛФХ.
При ξ=0 звено – консервативное,
графики АЧХ и ЛАХ будут иметь разрыв
на частоте
![]() ;
а график ЛФХ будет иметь вид прямых
линий.
;
а график ЛФХ будет иметь вид прямых
линий.



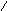 L(w), дб
L(w), дб ![]()
![]()
![]() w
w


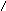 w0
w0 



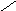



![]()
![]()
![]()
![]()
![]()


 K
K



![]()
![]()
lgw, дек
0 w0
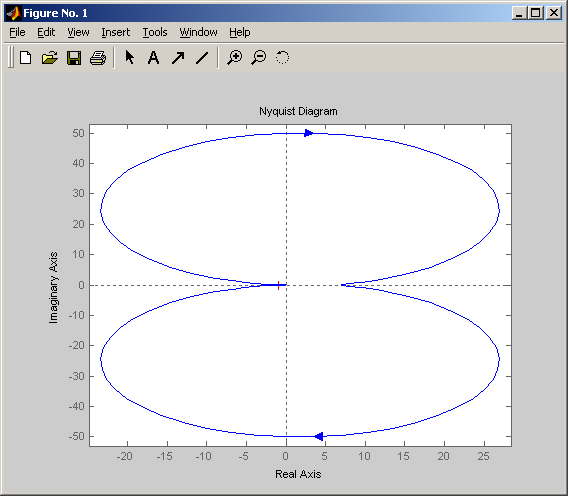
Амплитудно-фазовая частотная характеристика колебательного звена имеет вид:
![]()
![]()
Амплитудно-фазовая частотная характеристика
 Im
Im
K



 w=∞
w=0 Re
w=∞
w=0 Re

![]()
 A
w
A
w
![]()
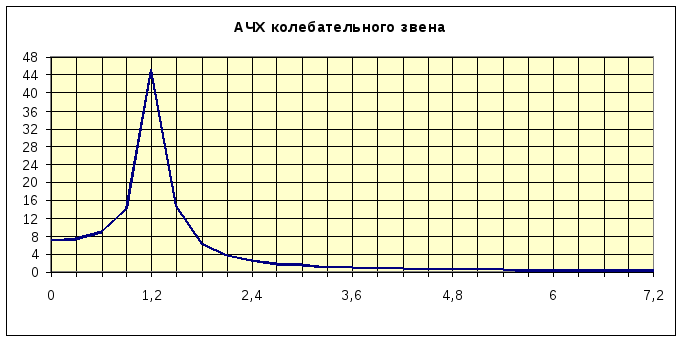
АЧХ может иметь резонансный
пик. Исследование модуля частотной
передаточной функции на максимум
показывает, что пик будет существовать
при ξ<3,84. Высота пика будет тем больше,
чем меньше параметр затухания:
![]()
Максимуму АЧХ соответствует
частота
![]()
АЧХ колебательного звена описывается выражением:
![]()
![]()
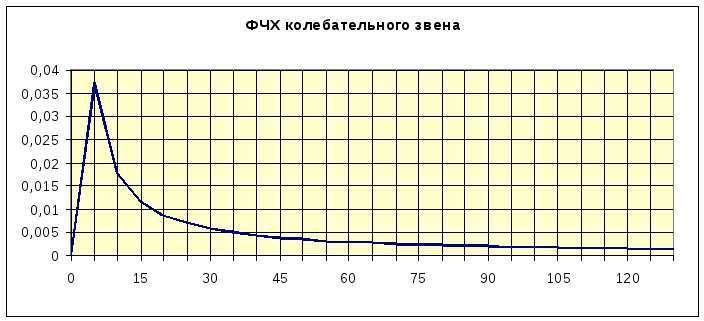
Фазо-частотная характеристика колебательного звена описывается выражением:
![]()
![]()
2.2. Интегрирующие звенья
2.2.1. Идеальное интегрирующее звено
Данное звено имеет передаточную функцию
![]()
![]()
Временные характеристики
Переходная функция идеального интегрирующего звена
![]()
![]()
Переходная

Весовая

Частотные характеристики
Логарифмическая амплитудная и фазовая частотные характеристики
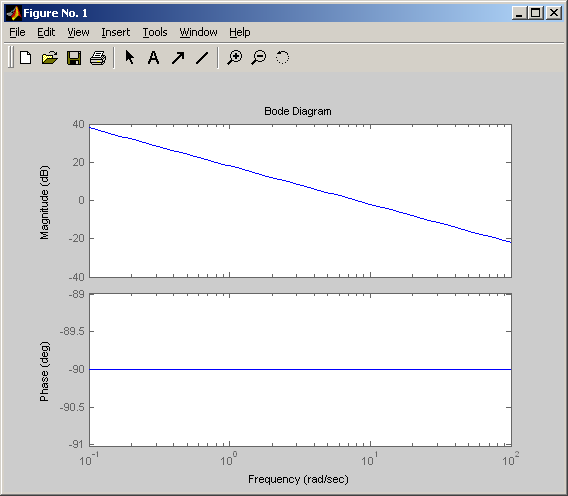
Амплитудно-фазовая частотная характеристика имеет вид:
![]()
Амплитудно-фазовая частотная характеристика

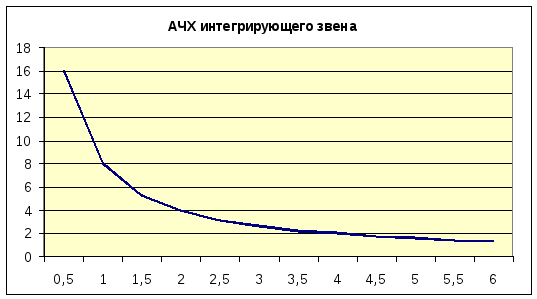
АЧХ интегрирующего звена описывается выражением:
![]()
![]()
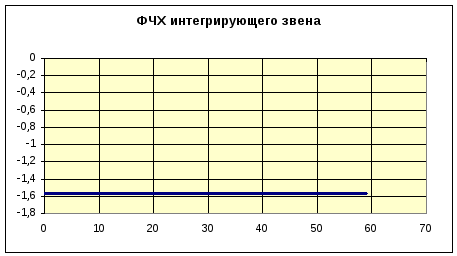
ФЧХ интегрирующего звена описывается выражением:
![]()
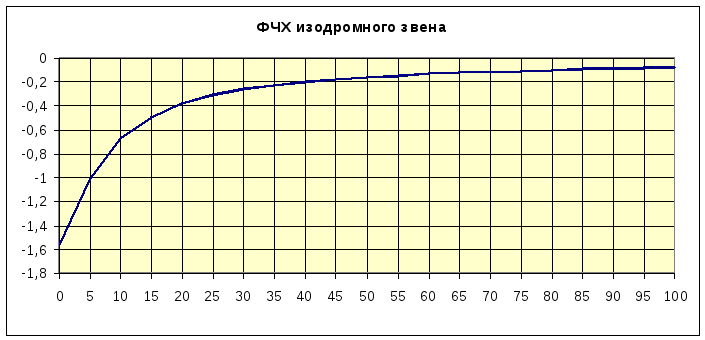
2.2.2. Изодромное звено (пропорционально-интегрирующее звено)
Это звено имеет передаточную функцию
![]()
![]()
т.е. его можно представить как параллельное соединение интегрирующего и пропорционального (безынерционного) звеньев. После простых преобразований это звено можно также записать в виде:
![]()
![]() (2)
(2)
где (1+τs) - форсирующее звено, τ =K2/K1.
Таким образом, в соответствии с (2) изодромное звено может быть также представлено как последовательное соединение интегрирующего и форсиру-ющего звеньев.
Временные характеристики
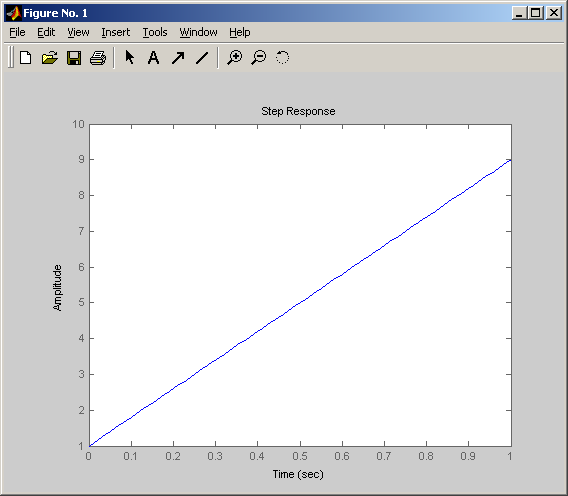
Переходная функция пропорционально-интегрирующего звена
![]()
![]()
Переходная
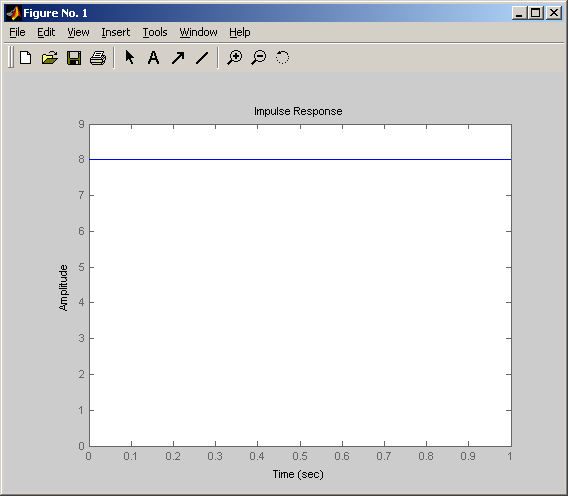
Весовая (импульсная переходная)
Частотные характеристики
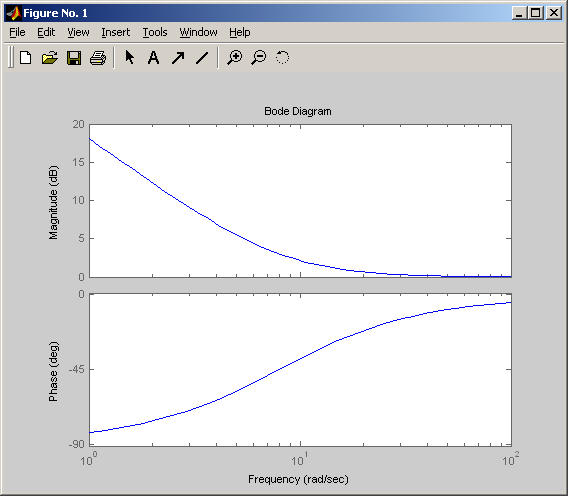
Логарифмическая амплитудная и фазовая частотные характеристики
Амплитудно-фазовая частотная характеристика
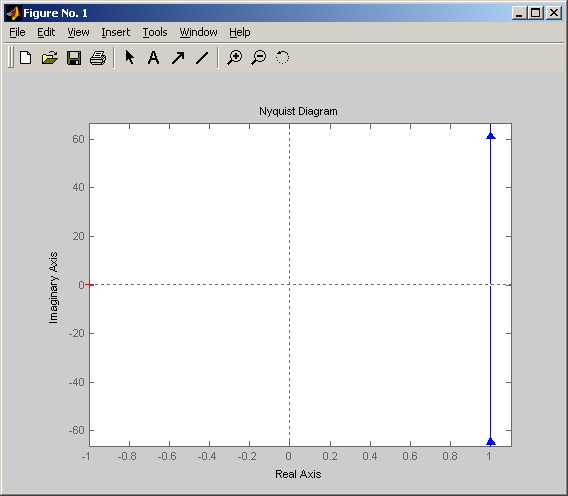
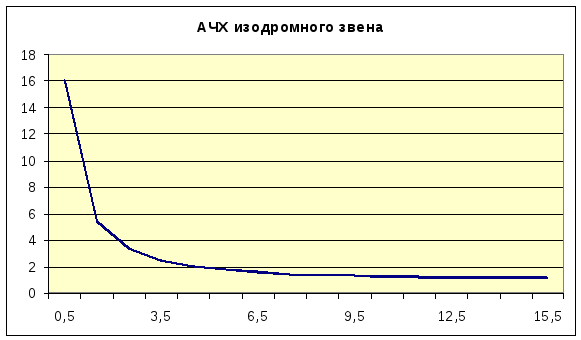
Поскольку изодромное звено может быть также представлено как последовательное соединение интегрирующего и форсирующего звеньев, АЧХ изодромного звена описывается выражением:
![]()
![]()
ФЧХ изодромного звена описывается выражением:
![]()
![]()