Биоэлектрическая модель

В основе электрических процессов и явлений, протекающих в живых системах, лежат механизмы, раскрытие которых возможно на клеточном и субклеточном уровнях. Для исследования биоэлектрических систем, наряду с биофизикой, эффективно используются законы, методы и язык теории электрических цепей.

В качестве объекта моделирования рассматривается мышца сердца, которая сокращается с определенной частотой, задаваемой особыми активными областями, называемыми водителями ритма сердца (ВСР), которым присуща автоматия, являющаяся свойством тканевых образований. В сердце млекопитающих существует несколько областей, обладающих ритмической автоматией. К таким областям относятся синоаурикулярный (синусный) SA — и атриовентрикулярный AV — узлы, а также некоторые другие тканевые структуры.

Основным водителем ритма здорового сердца (норма) является SA — узел. Тканевая структура SA — узла представляет собой скопление электрически активных клеток, обладающих ритмической автоматией. Между внешней и внутренней поверхностями мембраны такой клетки существует разность потенциалов Um, называемая мембранной ЭДС. По своей природе мембранная ЭДС является диффузионной и имеет ионный механизм возникновения. Значения Um определяются избирательной проницаемостью мембраны к отдельным ионам в различные фазы сердечного цикла.

В соответствии с мембранной теорией биоэлектрических процессов разность потенциалов Um определяется ионными токами. В общем случае клеточная мембрана проницаема для ионов и некоторых других.

Внешняя среда по отношению к клетке является поставщиком электрической энергии. Электрические параметры внеклеточной среды в определенных пределах можно считать инвариантными по отношению к клетке. В этом случае возможно рассмотрение схемы замещения возбудимой клеточной мембраны, предложенной Ходжкиным и Хаксли (рис. 4).

Рис. 4. Электрическая схема замещения возбудимой клеточной мембраны

Примером электрической модели клетки ВРС может служить модель, основанная на реализации нелинейного дифференциального уравнения 2-го порядка, к которому сводится описание электродинамики клетки ВРС по Ходжкину — Хаксли. Преобразование системы уравнений Ходжкина — Хаксли приводит к известному уравнению Ван дер Поля:

. (36)

Аналитическая реализация непрерывной нелинейной математической модели

Уравнение Ван дер Поля не имеет общего решения, которое можно было бы представить аналитически; существуют различные приближенные методы для оценки его вида (например, приближенный метод Ляпунова — Боголюбова). Однако наиболее удобным и обобщенным является использование фазовой плоскости для анализа поведения решения в окрестности некоторой точки.

Принципиально выделяется 2 вида точек фазовой плоскости:

1. обыкновенные точки;

2. особые точки (точки покоя).

Обыкновенные точки характеризуются единственностью проходящих через них фазовых траекторий, в то время как особые точки позволяют выделить семейства фазовых траекторий и поэтому представляют больший интерес.

В общем случае нелинейное дифференциальное уравнение второго порядка имеет вид:

(37)

равносильно системе уравнений второго порядка

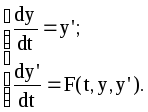(38)

Общее решение системы y = y(t), y’ = y’(t) может быть пред­ставлено геометрически семейством ориентированных фазовых траекторий на фазовой плоскости Oyy’.

Применительно к уравнению Ван дер Поля получается автономная система дифференциальных уравнений, т.е. система, в которой функции Q(y, y’) и P(y, y’) явно не зависят от параметра t:

(39)

Для возможности исследования автономной системы ее следует линеаризовать в точке покоя.

При этом, если у автономной системы существует точка покоя, то

P(y, y’) = Q(y, y’) = 0. (40)

Очевидно, что для уравнения Ван дер Поля это условие выполняется в точке (0,0).

Линеаризация заключается в разложении правых частей дифференциальных уравнений системы по формуле Тейлора. Тогда для эквивалентной уравнению Ван дер Поля системы получим:

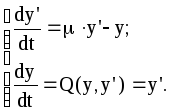(41)

Характер точки покоя полученной системы зависит от корней характеристического уравнения:

(42)

т.е., определяется значением коэффициента m.

Характер фазовой траектории в окрестности обыкновенной точки определяется только характером полученных траекторий в точке покоя, т.е. при фиксированном m невозможно выделить точки на плоскости, в окрестностях которых фазовая траектория будет иметь характер, отличный от траектории в точке покоя.

Замечание: при анализе характера точки покоя в случае , следует учитывать, что матрица А характеристического уравнения является недиагонализуемой, т.е. не существует матрицы С такой, что

или (43)

где и эмиртовые матрицы (точнее матрица А диагонализуема только в случае m = 0).