Лабораторная работа №5 Синтез регуляторов методами модального управления
Цель работы: выбрать структуру и рассчитать параметры
регулятора методом модального управления
Введение
Нули и полюсы передаточных функций линейных стационарных систем или собственные числа соответствующих матриц играют большую роль при описании их статических и динамических свойств. При этом метод синтеза, обеспечивающий заданное распределение корней характеристического уравнения замкнутой системы управления на комплексной плоскости, получил название метода стандартных коэффициентов. Сюда же можно отнести и методы синтеза, основанные на частотных характеристиках и корневом годографе. Эти методы обычно называют классическими или традиционными. Отличительной особенностью этих методов является грубость, что означает нечувствительность характеристик замкнутой системы к небольшим изменениям её параметров. В основу методов положена информация о передаточной функции и частотных характеристиках рассматриваемой системы.
В последние годы разработаны новые методы синтеза, которые принято называть методами современной теории управления. Они в большей степени зависимы от точности модели системы. Рассмотрим один из них, основанный на переменных состояния.
Пусть модель объекта задана в переменных состояния
dx / dt = Ax + Bu;
y = Cx.
Здесь х – вектор состояния размерности n ´ 1, компонентами которого являются переменные состояния системы n-го порядка; А – матрица состояния (n ´ n); В – матрица входа (n ´ m), где m – число управляющих воздействий; u – вектор входа размерности (m ´ 1), компонентами которого являются входные переменные системы; y – вектор выходных переменных размерностью р ´ 1, где р – число выходных переменных; C – матрица выхода (p ´ n),
Требуется найти управление
u = – К x,
такое, чтобы все или часть собственных чисел (мод) матрицы А – ВК замкнутой системы имели заданные значения или принадлежали заданному множеству.
Действительно, уравнение замкнутой системы
dx / dt = Ax + Bu = ( А – ВК ) х = Н х
и её характеристическое уравнение
det [pI – A + BK ] = 0.
Управление, основанное на применении алгебры собственных чисел передаточных матриц линейных стационарных систем, называется модальным управлением. Вектор К есть вектор постоянных коэффициентов размерностью m ´ n .
Задача синтеза заключается в определении желаемого положения корней характеристического уравнения замкнутой системы (рис. 1) и нахождении коэффициентов обратных связей Кij, обеспечивающих заданное размещение корней.
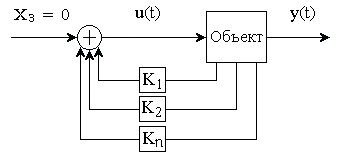
Рис. 1
Можно предположить, что вход системы равен нулю. Тогда и выходная величина должна быть равна нулю. На практике система подтверждена влиянию возмущений, которые стремятся сделать выход объекта отличным от нуля. Цель обратной связи по переменным состояния – вернуть значения выходной переменной и всех переменных состояния к нулю заданным образом. Система такого типа при нулевом или постоянном входном сигнале называется регулятором состояния.
При этом возникает необходимость измерения всех или почти всех переменных состояния. Те переменные, которые не могут быть измерены непосредственно, подлежат оценке на основании измеряемых переменных. Системы используют обратную связь по состоянию и синтез регуляторов связан с понятиями наблюдаемость и управляемость.
Говорят, что система, описываемая матрицами (А, В) называется управляемой, если существует такое неограниченное управление u, которое может перевести систему из произвольного начального состояния x (0) в любое другое заданное состояние х (Т) за конечное время Т. Если матрица
[B AB A2 B …An-1B]
имеет себе обратную, то система управляема.
Для системы с одним входом и одним выходом вводится понятие матрицы управляемости РС , которая выражается через А и В как
РС = [B AB A2 B …An-1B]
и имеет размерность n ´ n. Если определитель матрицы РС отличен от нуля, то система является управляемой.
Линейная стационарная система является наблюдаемой, если по значениям выходной функции y(t) можно определить начальное состояние х(0) за конечное время Т. Если матрица
Q = [C CA CA2 …CAn-2 CAn-1]T
имеет себе обратную, то система наблюдаема.
Наблюдаемость связана с оценкой переменных состояния. Если каждая переменная состояния вносит свой вклад в выходной сигнал системы, то система может быть наблюдаемой. Это эквивалентно тому, что на модели системы в виде графа от каждой переменной состояния существует путь к выходной переменной.
В большинстве систем, являющихся либо неуправляемыми, либо ненаблюдаемыми, либо то и другое, происходит сокращение нуля и полюса. Следовательно, в результате такого сокращения модель системы имеет более низкий порядок. Система, в которой число переменных состояния больше, чем её минимальный порядок, будет либо неуправляемой, либо ненаблюдаемой, либо то и другое.
Все корни характеристического уравнения можно разместить на комплексной плоскости в заданных точках только в том случае, когда система является наблюдаемой и управляемой.
Матрица системы с обратной связъю имеет вид
Желаемое характеристическое уравнение системы можно записать в виде
D(p) = p n + a n-1 p n-1 + … + a1 p + a0 .
В соответствии с процедурой синтеза путём размещения полюсов необходимо найти такую матрицу К, чтобы выполнялось равенство
det ( pI – А + ВК ) = p n + a n-1 p n-1 + … + a1 p + a0 .
Это уравнение содержит n неизвестных Кi . Приравнивая в этом уравнении коэффициенты при одинаковых степенях р, мы получим n уравнений относительно n неизвестных. В дальнейшем ограничимся системами с одним входом и одним выходом, поэтому u(t) и y(t) есть скалярные переменные. Закон управления можно записать в виде
u(t) = – K1x1(t) – K2x2(t) – … – Kn xn(t).
Отсюда видно, что сигнал, поступающий на вход объекта, представляет собой линейную комбинацию всех переменных состояния. Следовательно, и уравнения относительно неизвестных Кi будут линейными.
Для систем третьего порядка желательно, чтобы характеристический полином имел вид
(p2 + 2zwp + w2) (p + xw),
где w – собственная частота; ζ - декремент затухания. Это обеспечивает быстрое нарастание переходного процесса и малое перерегулирование, если принять z = 0,707. Собственную частоту рассчитывают по выражению
tP = 4/(zw) ,
где tP – время регулирования.
Для систем с одним входом и одним выходом матрицу коэффициентов обратной связи по состоянию К = [ К1 К2 … Кn ] , с помощью которой формируется управляющий сигнал u = – Kx, можно определить по формуле Аккермана. Если задан желаемый характеристический полином замкнутой системы
q(p) = pn + a1 pn-1 + … + an ,
то матрица коэффициентов обратной связи по состоянию
,
где q(A) = An + a1 An-1 + … + an-1 A + an I.
Рассмотрим систему, представленную на рис. 2.
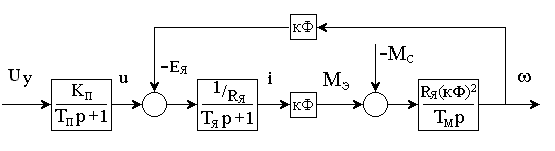
Рис. 2
В качестве переменных состояния выбираем угловую скорость w, ток якоря i и напряжение на выходе тиристорного преобразователя u,. Тогда уравнения в переменных состояния можно представить в виде:
dw /dt = (кФ/J) i
di /dt = (–кФ/ LЯ) w + (– RЯ / LЯ) i + ( 1 / LЯ) u ;
du /dt = (–1/ TП ) u + (KП / TП ) UУ ;
Отсюда следует, что матрицы
.
Пусть КП = 23; кФ = с = 1,36; J = 1,3 ; RЯ = 0,116 Ом;
ТЯ = 0,06 с ; ТП = 0,01 с; ТМ = 0,0815 с; LЯ = 0, 00696 Гн;
желаемый характеристический полином
q(p)= p3 + 84,9p2 +3230p +45280
Тогда
.
Все остальные вычисления необходимо выполнить в MATLAB.
>> A=[0 1.046 0;-195.402 -16.667 143.678;0 0 -100]
A =
0 1.0460 0
-195.4020 -16.6670 143.6780
0 0 -100.0000
>> B=[0;0;2300]
B =
0
0
2300
>> Pc=[B A*B A*A*B]
Pc =
1.0e+007 *
0 0 0.0346
0 0.0330 -3.8554
0.0002 -0.0230 2.3000
>> det(Pc)
ans =
-2.6272e+014
>> Pci=inv(Pc)
Pci =
0.0048 0.0003 0.0004
0.0003 0.0000 0
0.0000 0 0
>> I=eye(3)
I =
1 0 0
0 1 0
0 0 1
>> q=A*A*A+84.9*A*A+3230*A+45280*I
q =
1.0e+005 *
0.3133 0.0198 -0.0477
-3.6899 -0.0014 7.2774
0 0 -4.2872
>> K=[0 0 1]*Pci*q
K =
0.0906 0.0057 -0.0138
Структурные схемы математических моделей двигателя и системы автоматического управления с обратными связями представлены на рис. 3.
Рис. 3
1. Собрать структурную схему двигателя (рис. 2, 3) в MATLAB, проверить её работу и откорректировать математическую модель двигателя в соответствии с данными варианта. Снять переходную характеристику прямого пуска двигателя в MATLAB. Данные для моделирования приведены в таблице 1.
Электромеханическую
постоянную рассчитать по формуле
.
Таблица 1.
|
№ |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
Тп, c |
0,01 | |||||||||
|
Кп |
23 |
46 |
23 |
46 |
23 |
46 |
23 |
46 |
23 |
46 |
|
Lя,мГн |
6,9 |
7,4 |
8,2 |
7,1 |
7,7 |
7,9 |
8,0 |
6,5 |
6,8 |
8,4 |
|
Rя, Ом |
0,11 |
0,14 |
0,13 |
0,12 |
0,16 |
0,19 |
0,22 |
0,18 |
0,21 |
0,20 |
|
С, В*с |
1,3 |
1,2 |
1,4 |
1,34 |
1,36 |
1,18 |
1,45 |
1,54 |
1,61 |
1,65 |
|
J,кг*м2 |
2,0 |
2,2 |
2,5 |
1,4 |
1,9 |
2,8 |
1,7 |
1,5 |
2,1 |
2,3 |
2. Для системы (рис. 3) рассчитать коэффициенты обратных связей и выполнить моделирование в MATLAB. Определить время регулирования и перерегулирование. Расчётное время переходного процесса tP принять равным (4 - 8)ТП . Сравнить переходные процессы при изменении задания и нагрузки с прямым пуском двигателя.
3. Если к системе предъявляется требование астатизма как по постоянному входному сигналу, так и по нагрузке, то этого можно добиться только с помощью ПИ – регулятора (рис. 4), при этом порядок n системы увеличивается на единицу.
Рис.
4
Синтез регулятора осуществим также методом размещения полюсов. Задачу целесообразно решать при наличии единичной обратной связи по скорости.
Уравнения состояния и входной сигнал объекта
dx / dt = Ax + Bu;
y = Cx = [1 0 0 0] x1;
u = –Kx – K4x4;
dx4/dt = x1 – U,
где x4 – выходная координата интегратора ПИ – регулятора.
Данную систему уравнений можно представить в виде
dxf
/dt
= Af
xf
– Bf
Kf
xf
+
U,
где
или
Этому уравнению соответствует характеристическое уравнение
Желаемое характеристическое уравнение зададим в виде полинома Баттерворта четвёртого порядка (время переходного процесса t п @ 0, 12с):
Матричный полином, образованный путём использования коэффициентов желаемого характеристического уравнения
.
Программа определения коэффициентов в MATLAB
>> Af=[0 1.046 0 0;-195.402 -16.667 143.678 0;0 0 -100 0;1 0 0 0]
Af =
0 1.0460 0 0
-195.4020 -16.6670 143.6780 0
0 0 -100.0000 0
1.0000 0 0 0
>> Bf=[0;0;2300;0]
Bf =
0
0
2300
0
>> Pc=[Bf Af*Bf Af*Af*Bf Af*Af*Af*Bf]
Pc =
1.0e+009 *
0 0 0.0003 -0.0403
0 0.0003 -0.0386 3.8796
0.0000 -0.0002 0.0230 -2.3000
0 0 0 0.0003
>> det(Pc)
ans =
-9.0812e+019
>> Pci=inv(Pc)
Pci =
0.0048 0.0003 0.0004 0.0591
0.0003 0.0000 0 0.0054
0.0000 0 0 0.0003
0 0 0 0.0000
>> I=eye(4)
I =
1 0 0 0
0 1 0 0
0 0 1 0
0 0 0 1
>> q=Af^4+174*Af^3+15156*Af^2+773333*Af+19753086*I
q =
1.0e+008 *
0.1723 0.0056 0.0099 0
-1.0467 0.0830 -0.1780 0
0 0 0.1998 0
0.0074 0.0001 0.0001 0.1975
>> K=[0 0 0 1]*Pci*q
K =
2.1442 0.0373 0.0249 57.1459
Структурная схема системы управления с ПИ-регулятором представлена на рис. 5.
Рис. 5
Результаты расчётов были проверены в системе MATLAB 6.5 + Simulink 4 (рис. 6).
Время, с
Рис. 5
Рис. 13.8. 1 – прямой пуск; 2 – с обратными связями; 3 – с ПИ – регулятором
